前言:本文主要围绕 Matlab 的实现展开,Java版本以及Python版本参考文章最后的源码地址,MatLab和python实现大致相同,Java较为不同。
我们了解过深度学习的都知道,我们在进行网络优化的过程都是通过反向传播求导进行参数的不断优化,而这种类型的优化参数采用前向传播的方式继续优化网络,不断找出最优解,或者最优的参数。很多的优化算法都来自于大自然的启发,来一种算法叫做蚁群算法,灵感就是来自于蚂蚁,所以观察大自然有时也是灵感的来源。
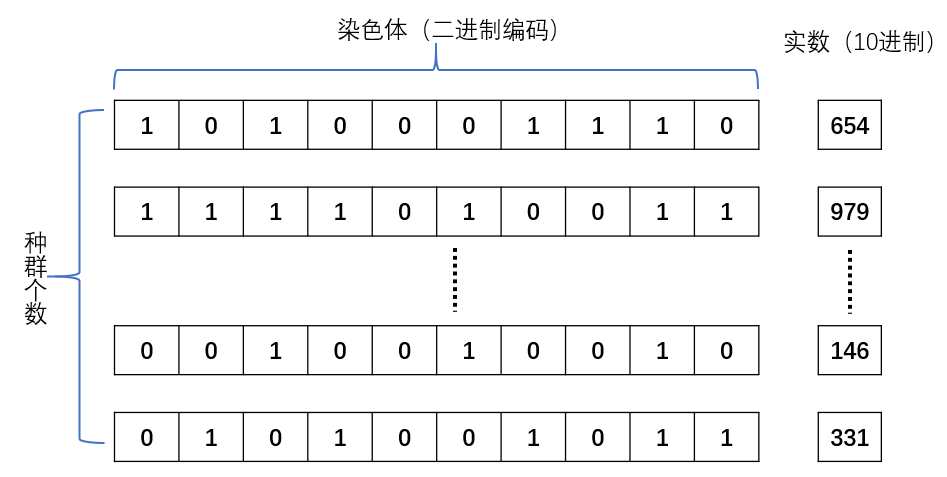
遗传算法,也叫Genetic Algorithm,简称 GA 算法他既然叫遗传算法,那么遗传之中必然有基因,那么基因染色体(Chromosome)就是它的需要调节的参数。我们在生物中了解到,大自然的法则是“物竞天择,适者生存”,我觉得遗传算法更适用于“优胜劣汰”。
- 优:最优解,
- 劣:非最优解。
下面主要通过疑问提问题的方式进行解释遗传算法当中的适应度函数、选择、交叉、变异这几个名词。
1. 都知道优胜劣汰,那怎么实现优胜劣汰呢? 很重要的一个环节就是选择,也称之为“大自然的选择”,大自然怎么选择呢,大自然会抛弃掉一些适应能力差的,在程序当中就是离最优解较远的解,会被抛弃掉。
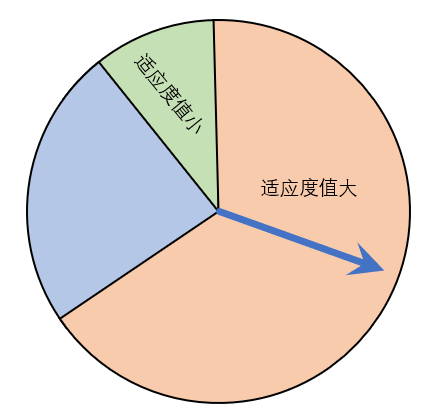
2. 如何实现大自然的选择呢? 这里我们会引入轮盘赌法,进行大自然的选择。选择一些离最优解较近的个体。还有一些其他的经典的选择办法,例如锦标赛法进行选择。
3. 只靠选择就可以实现吗?那样会不会陷入局部最优解? 如果只靠选择进行调优,那么最终的结果会受到初始种群的影响,只是在初始种群的群体中进行选择,得出的最优解也是在初始群体中的最优解。所以就需要引入大自然当中的“啪啪啪”,也叫交叉。正所谓“龙生龙,凤生风,老鼠生下来就会打洞”,所以说两个优秀的基因进行交叉可以将两者优秀的基因遗传给一代,也增加了群体的基因多样性,但这种不一定就是最好的,也可能发生“夭折”。
4. 大自然的选择好像不仅如此,还有变异吧? 为了更好的模拟大自然的选择规律,来需要进入变异,变异发生的概率很低,但也是增加群体多样性的条件,和交叉相同,变异求解出来的不一定是最好的解,也会出现“夭折”。
5. 上面只是大自然的规则,那么大自然的环境又是什么呢? 优秀的基因并不是独立的,就像北极熊不会存活在热带雨林一样。只有适合环境的基因才是优秀的,所以说基因具有相对性,环境是挑选基因的先决条件,这里的环境就是适应度函数。个体用过适应度函数后得到的结果越大,表明更加适合这里的环境,那么保留下来的概率越大。反之则越小。
正所谓 “不结合代码的解释都是** ” 。下面结合代码来梳理遗传算法的实现。
涉及到还是适应度函数、选择、交叉、变异这几个模块。下面就这几个模块展开说明。具体的流程图解释如下:
- 需要先对初始种群进行一次适应度函数进行计算,这样方便我们对个体进行选择,适应度值越大的越容易被保留;
- 对群体进行选择,选择出适应度值较大的一部分优势群体;
- 对优势种群进行 “交配”,更容易产生优秀的个体;
- 模拟大自然变异操作,对染色体个体进行变异操作;
下面以计算函数最大值 $$ f(x)=10\times sin(5\times x)+7\times \left|x-5\right|+10; x\in[0, 10] $$
种群的初始化相对简单,只需要随机生成一个二维矩阵,矩阵的size=(种群大小,染色体编码长度)。染色体编码采用二进制编码的方式。染色体编码并不是直接采用将[0, 10]直接转换为二进制,原因如下:
- 并非均匀分布,10的二进制表示为1010,会导致出现空余位置,例如11、12等没有意义的数字出现
- 精度低,如果直接编码最小增量单位变成了 1 ,没有了浮点数的表示,最优解很多情况都会出现在浮点数的表示范围。n:代表染色体编码的长度
$$ x = \dfrac{染色体编码对应的十进制值}{2^n - 1} $$ 此时x的范围为[0, 1],我们可以根据待测得x轴的范围进行偏移计算。例如:x得范围为[2, 10],则设计:
$$ x = \dfrac{染色体编码对应的十进制值}{2^n - 1} \times 8 + 2 $$ 种群初始化基本结构如下,实数范围还需要进一步计算得到真正得x轴的浮点值。
```matlab % popsize: 种群个数 % chromlength: 染色体长度 function pop=initpop(popsize,chromlength) % round:产生的随机数进行四舍五入操作就是0或者1 pop = round(rand(popsize,chromlength)); ```适应度函数得出的值越大表明个体越优秀,所以一般情况下,在求解函数最大值的时候,适应度函数就是求解函数本身,求解最小值的时候适应度函数就是函数的倒数。在本例中求取最大值,所以适应度函数就是函数本身。
function [objvalue] = cal_objvalue(pop)
x = binary2decimal(pop);
objvalue=10*sin(5*x)+7*abs(x-5)+10;
% 二进制转10进制并转换到对应的x轴浮点值
function pop2 = binary2decimal(pop)
[px,py]=size(pop);
for i = 1:py
pop1(:,i) = 2.^(py-i).*pop(:,i);
end
temp = sum(pop1,2);
pop2 = temp*10/1023; % 限制到[0, 10]我们在前面已经说明了选择的原因(挑选优秀个体),挑选的算法有很多,我们这里选择“轮盘赌法”。轮盘赌法就是类似于我们玩的转盘,圆心角度越大的我们越容易选中。 注: 选择后后的个体数目和原种群个数相同。
大自然就像那个指针,适应度值越大,表明这个体约适应这个环境,那么被选择的概率越大,与此同时,适应度值小的个体并不代表不会被选中,只是选中的概率小,一方面也保证了正负样本的一个均衡。
% pop: 遗传算法的种群
% fitvalue: 种群的适应度值
% newpop: 返回筛选过后的新的种群
function [newpop] = selection(pop,fitvalue)
[px,py] = size(pop);
totalfit = sum(fitvalue);
% 将适应度值转换为概率,适应度值越大表明概率越大
p_fitvalue = fitvalue/totalfit;
% 沿梯度进行求和运算 [0.1, 0.3, 0.6] ->[0.1, 0.4, 1]
p_fitvalue = cumsum(p_fitvalue);
% ms相当于指针,得出落在哪一个区域,就表明这个基因被选中
ms = sort(rand(px,1)); % 先进行排序,减小时间复杂度
fitin = 1; % 适应度矩阵的索引
newin = 1; % 新种群索引
while newin<=px
if(ms(newin))<p_fitvalue(fitin) % 表明落在了这一个区域
newpop(newin,:)=pop(fitin,:);
newin = newin+1;
else
fitin=fitin+1;
end
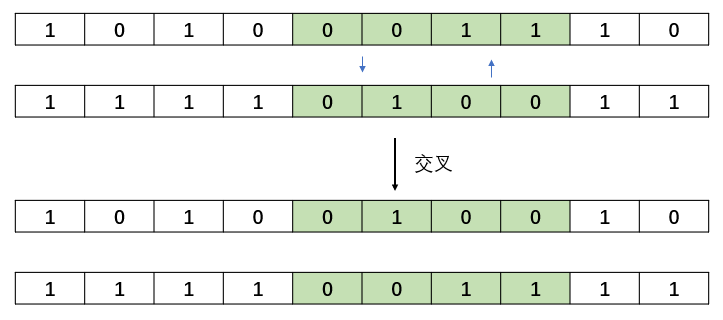
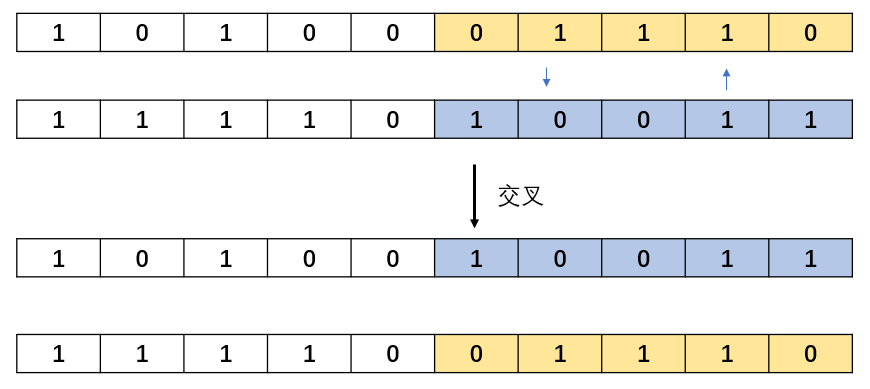
end交叉相对来说,比较简单,就是将两个染色体进行基因片段的交叉。交叉的方式有很多,可以单个点进行交叉,随机基因片段交叉,随机长度的交叉方式,在这里仅实现随机长度的交叉方式。 随机长度交叉:
随机距离交叉(本例实现):
程序实现:
% pop:总种群
% pc:交叉概率
function [newpop] = crossover(pop,pc)
[px,py] = size(pop);
newpop = ones(size(pop));
% 每两个进行一次交叉
for i = 1:2:px-1
if(rand<pc)
% 随机产生分割点
cpoint = round(rand*py);
newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
else
newpop(i,:) = pop(i,:);
newpop(i+1,:) = pop(i+1,:);
end
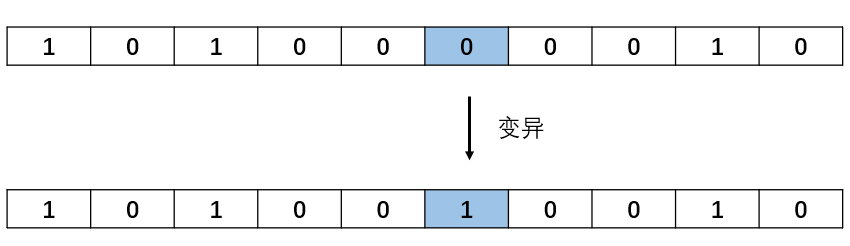
end变异就变得更加简单,对于二进制编码,只需要将随机一个基因位置进行取反操作。
程序实现:
% pop: 总种群
% pm: 变异概率
function [newpop] = mutation(pop,pm)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
if(rand<pm)
mpoint = round(rand*py);
if mpoint <= 0 % matlab数组索引从 1 开始
mpoint = 1;
end
newpop(i,:) = pop(i,:);
if newpop(i,mpoint) == 0
newpop(i,mpoint) = 1;
else newpop(i,mpoint) == 1
newpop(i,mpoint) = 0;
end
else newpop(i,:) = pop(i,:);
end
end主函数主要是围绕下面的流程图进行计算。
程序实现:
clear;
clc;
% 总种群数量
popsize=100;
% 染色体长度
chromlength=10;
% 交叉概率
pc = 0.6;
% 变异概率
pm = 0.001;
%初始化种群
pop = initpop(popsize,chromlength); % 100 * 10
for i = 1:100
objvalue = cal_objvalue(pop);
fitvalue = objvalue;
newpop = selection(pop,fitvalue);
newpop = crossover(newpop,pc);
newpop = mutation(newpop,pm);
pop = newpop;
[bestindividual,bestfit] = best(pop,fitvalue);
x2 = binary2decimal(bestindividual); % 最优解 x 值
x1 = binary2decimal(newpop);
y1 = cal_objvalue(newpop);
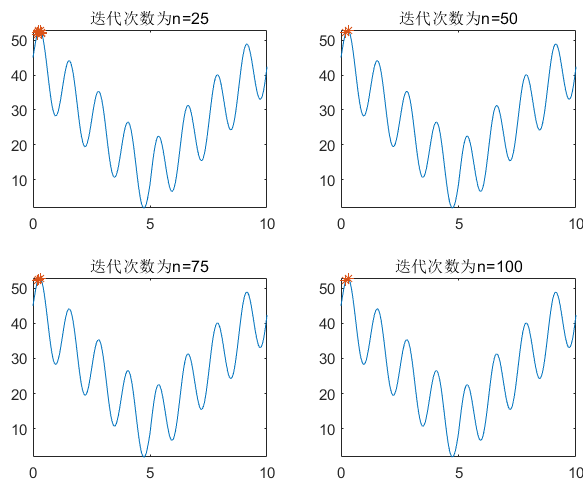
if mod(i,20) == 0
figure;
fplot(@(x)10*sin(5*x)+7*abs(x-5)+10,[0 10]);
hold on;
plot(x1,y1,'*');
title(['迭代次数:%d' num2str(i)]);
end
end
fprintf('The best X is --->>%5.2f\n',x2);
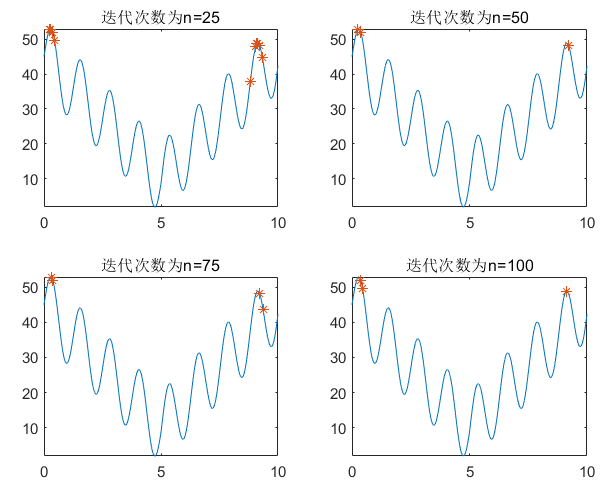
fprintf('The best Y is --->>%5.2f\n',bestfit);遗传算法同样会陷入局部最优解的情况,例如下面的情况:
解决局部最优解的方法有很多,小伙伴可以自行百度,我这里提供一种方法叫做非线性寻优,利用matlab自带函数fmincon进行非线性寻优。