-
Notifications
You must be signed in to change notification settings - Fork 626
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Accuracy of adjoint gradients in 3D #2757
Comments
|
Can you try with |
That did it! Increasing the resolution to 25 (from 20) and setting I have updated the original script with these changes. Now onto a broad bandwidth simulation... |
|
Great! We should probably set |
|
Here is another unit test for the adjoint gradients in 3D based on computing the diffraction efficiency of a transmitted order in air of a 2D binary grating on a substrate given a planewave at normal incidence. The 2D design region is extruded in the Results from running this test for S and P polarizations demonstrate good agreement in the directional derivatives obtained from the adjoint gradients and finite difference. 1. S polarization 2. P polarization We will want to repeat this test using the import math
from typing import Tuple
from autograd import numpy as npa
import matplotlib
matplotlib.use('agg')
import matplotlib.pyplot as plt
import meep as mp
import meep.adjoint as mpa
import numpy as np
RESOLUTION_UM = 50
WAVELENGTH_UM = 0.5
DIFFRACTION_ANGLE_DEG = 35.0
DIFFRACTION_ORDER = 1
GRATING_PERIOD_X_UM = (DIFFRACTION_ORDER * WAVELENGTH_UM /
math.sin(math.radians(DIFFRACTION_ANGLE_DEG)))
GRATING_PERIOD_Y_UM = 0.5 * WAVELENGTH_UM
GRATING_HEIGHT_UM = 0.5
GRATING_DUTY_CYCLE = 0.5
DESIGN_REGION_SIZE = mp.Vector3(
GRATING_DUTY_CYCLE * GRATING_PERIOD_X_UM,
GRATING_DUTY_CYCLE * GRATING_PERIOD_Y_UM,
GRATING_HEIGHT_UM
)
DESIGN_REGION_RESOLUTION_UM = int(2 * RESOLUTION_UM)
NX = int(DESIGN_REGION_SIZE.x * DESIGN_REGION_RESOLUTION_UM) + 1
NY = int(DESIGN_REGION_SIZE.y * DESIGN_REGION_RESOLUTION_UM) + 1
S_POLARIZATION = True
def binary_grating_2d() -> mpa.OptimizationProblem:
"""Sets up the adjoint problem for a 2D binary grating."""
frequency = 1 / WAVELENGTH_UM
pml_um = 1.0
substrate_um = 3.0
padding_um = 3.0
pml_layers = [mp.PML(direction=mp.Z, thickness=pml_um)]
n_glass = 1.5
glass = mp.Medium(index=n_glass)
size_x_um = GRATING_PERIOD_X_UM
size_y_um = GRATING_PERIOD_Y_UM
size_z_um = pml_um + substrate_um + GRATING_HEIGHT_UM + padding_um + pml_um
cell_size = mp.Vector3(size_x_um, size_y_um, size_z_um)
k_point = mp.Vector3()
# The plane of incidence is XZ. This means Ey is the S polarization and
# Ex is the P polarization.
if S_POLARIZATION:
src_cmpt = mp.Ey
eig_parity = mp.ODD_Y
else:
src_cmpt = mp.Ex
eig_parity = mp.EVEN_Y
src_pt = mp.Vector3(0, 0, -0.5 * size_z_um + pml_um)
sources = [
mp.Source(
mp.GaussianSource(frequency, fwidth=0.1 * frequency),
component=src_cmpt,
center=src_pt,
size=mp.Vector3(size_x_um, size_y_um, 0),
)
]
matgrid = mp.MaterialGrid(
mp.Vector3(NX, NY, 1),
mp.air,
glass,
weights=np.ones((NX, NY)),
do_averaging=False,
)
matgrid_region = mpa.DesignRegion(
matgrid,
volume=mp.Volume(
center=mp.Vector3(
0,
0,
(-0.5 * size_z_um + pml_um + substrate_um +
0.5 * GRATING_HEIGHT_UM)
),
size=mp.Vector3(
DESIGN_REGION_SIZE.x,
DESIGN_REGION_SIZE.y,
GRATING_HEIGHT_UM
),
),
)
geometry = [
mp.Block(
material=glass,
size=mp.Vector3(mp.inf, mp.inf, pml_um + substrate_um),
center=mp.Vector3(
0, 0, -0.5 * size_z_um + 0.5 * (pml_um + substrate_um)
),
),
mp.Block(
material=matgrid,
size=matgrid_region.size,
center=matgrid_region.center,
),
]
sim = mp.Simulation(
resolution=RESOLUTION_UM,
cell_size=cell_size,
boundary_layers=pml_layers,
k_point=k_point,
sources=sources,
geometry=geometry,
)
tran_pt = mp.Vector3(0, 0, 0.5 * size_z_um - pml_um)
kdiff = mp.Vector3(
DIFFRACTION_ORDER / GRATING_PERIOD_X_UM,
0,
(frequency**2 - (DIFFRACTION_ORDER / GRATING_PERIOD_X_UM)**2)**0.5
)
print(f"kdiff = ({kdiff.x:.5f}, {kdiff.y:.5f}, {kdiff.z:.5f})")
obj_list = [
mpa.EigenmodeCoefficient(
sim,
mp.Volume(
center=tran_pt,
size=mp.Vector3(size_x_um, size_y_um, 0),
dims=3,
),
mode=1,
kpoint_func=lambda *not_used: kdiff,
eig_parity=eig_parity,
eig_vol=mp.Volume(
center=tran_pt,
size=mp.Vector3(1 / RESOLUTION_UM, 1 / RESOLUTION_UM, 0),
dims=3
),
),
]
def J(tran_mon):
return npa.abs(tran_mon)**2
opt = mpa.OptimizationProblem(
simulation=sim,
objective_functions=J,
objective_arguments=obj_list,
design_regions=[matgrid_region],
frequencies=[frequency],
)
return opt
if __name__ == "__main__":
opt = binary_grating_2d()
# ensure reproducible results
rng = np.random.RandomState(9861548)
# random design weights
initial_design_weights = 0.9 * rng.rand(NX * NY)
# constant design weights
# initial_design_weights = 0.9 * np.ones((NX * NY))
# random perturbation for design region
max_perturbation = 1e-5
random_perturbation = max_perturbation * rng.rand(NX * NY)
unperturbed_val, unperturbed_grad = opt(
[initial_design_weights],
need_gradient=True
)
perturbed_val, _ = opt(
[initial_design_weights + random_perturbation],
need_gradient=False
)
if unperturbed_grad.ndim < 2:
unperturbed_grad = np.expand_dims(unperturbed_grad, axis=1)
adj_directional_deriv = ((random_perturbation[None, :] @
unperturbed_grad).flatten())
fnd_directional_deriv = perturbed_val[0] - unperturbed_val[0]
print(f"directional-derivative:, {fnd_directional_deriv} "
f"(finite difference), {adj_directional_deriv[0]} (adjoint)") |
|
Can't we just make this cell much smaller? It can be a toy problem and still exercise the gradients. |
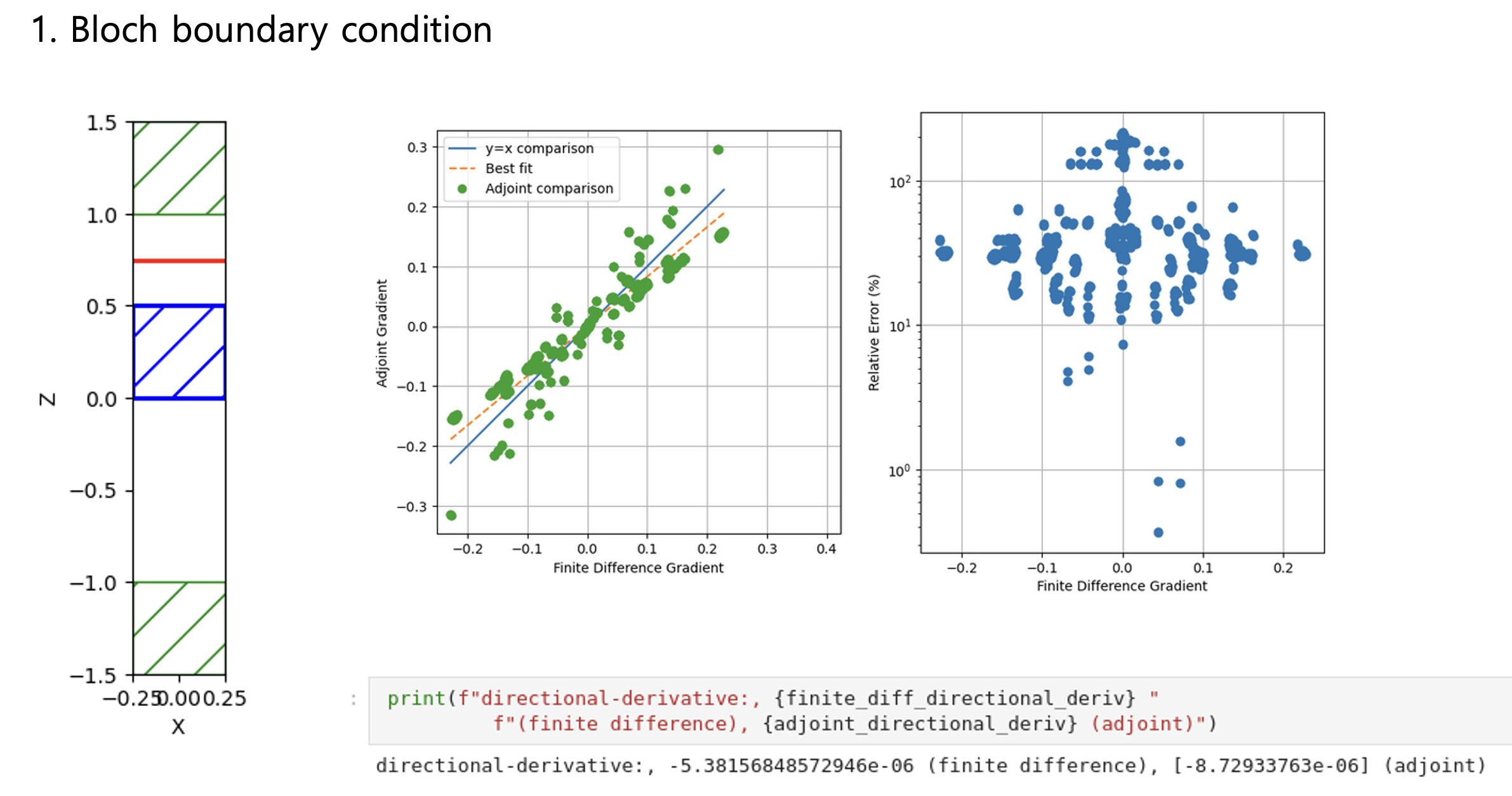
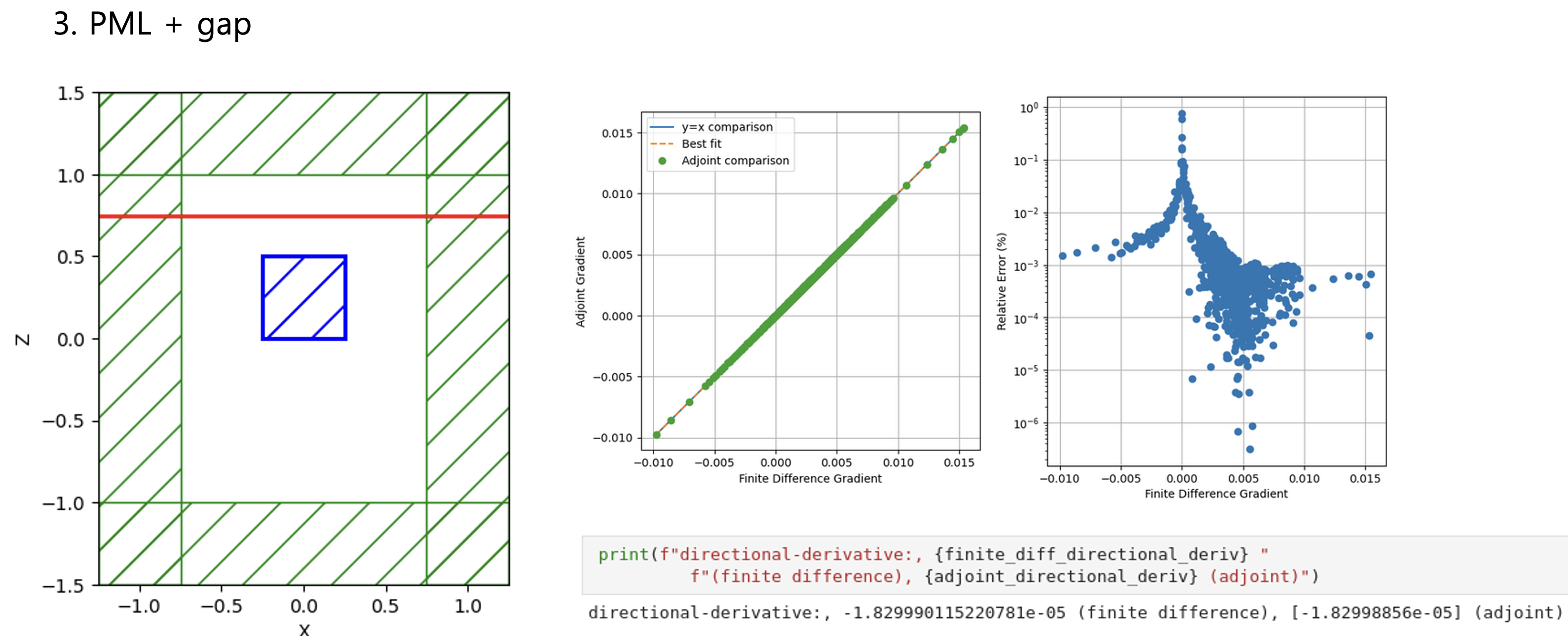
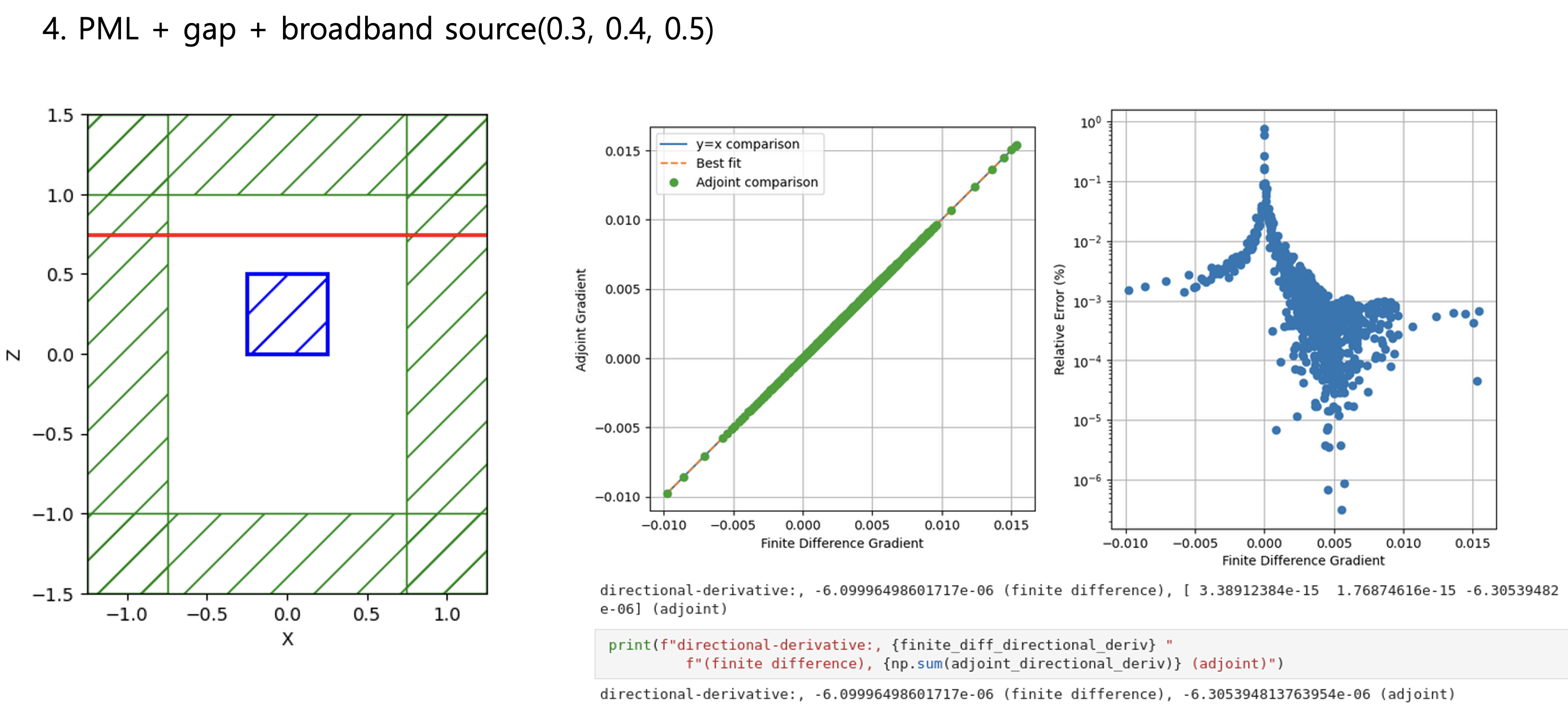
Python Meep: 3D adjoint gradient accuracy issueHello all, When I set all boundaries with PML, the accuracy of the adjoint gradient in 3D is correct.
Considering Fig. 1 ~ 4 results, the more unrelated the design region is to the boundary conditions, the more accurately the adjoint gradient is measured. Do you have any workarounds for these issues, or can you comment? Toy problem code - Bloch boundary condition"""Validates the adjoint gradient of a metalens in 3d."""
import meep as mp
import meep.adjoint as mpa
import numpy as np
from autograd import numpy as npa
from matplotlib import pyplot as plt
Air = mp.Medium(index=1.0)
SiN = mp.Medium(index=1.5)
resolution = 20
Lpml = 0.5
pml_layers = [mp.PML(thickness = Lpml, direction = mp.Z)]
Sourcespace = 0.5
design_region_width_x = 0.5
design_region_width_y = 0.5
design_region_height = 0.5
Sx = design_region_width_x
Sy = design_region_width_y
Sz = Lpml + design_region_height + Sourcespace + 1 + Lpml
cell_size = mp.Vector3(Sx, Sy, Sz)
wavelengths = np.array([0.5])
frequencies = 1/wavelengths
nf = len(frequencies)
design_region_resolution = int(resolution)
fcen = 1 / 0.5
width = 0.1
fwidth = width * fcen
source_center = [0, 0, Sz / 2 - Lpml - Sourcespace / 2 ]
source_size = mp.Vector3(Sx, Sy, 0)
src = mp.GaussianSource(frequency=fcen, fwidth=fwidth)
source = [mp.Source(src, component=mp.Ex, size=source_size, center=source_center,),]
Nx = int(round(design_region_resolution * design_region_width_x))
Ny = int(round(design_region_resolution * design_region_width_y))
Nz = int(round(design_region_resolution * design_region_height))
design_variables = mp.MaterialGrid(mp.Vector3(Nx, Ny, Nz), Air, SiN, grid_type="U_MEAN",do_averaging=False)
design_region = mpa.DesignRegion(
design_variables,
volume=mp.Volume(
center=mp.Vector3(0, 0, Sz / 2 - Lpml - Sourcespace - design_region_height/2),
size=mp.Vector3(design_region_width_x, design_region_width_y, design_region_height),
),
)
geometry = [
mp.Block(
center=design_region.center, size=design_region.size, material=design_variables
),
]
sim = mp.Simulation(
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
sources=source,
default_material=Air,
resolution=resolution,
k_point = mp.Vector3(0,0,0)
)
monitor_position_0, monitor_size_0 = mp.Vector3(-design_region_width_x/2, design_region_width_y/2, -Sz/2 + Lpml + 0.5/resolution), mp.Vector3(0.01,0.01,0)
FourierFields_0_x = mpa.FourierFields(sim,mp.Volume(center=monitor_position_0,size=monitor_size_0),mp.Ex,yee_grid=True)
ob_list = [FourierFields_0_x]
def J(fields):
return npa.mean(npa.abs(fields[:,1]) ** 2)
opt = mpa.OptimizationProblem(
simulation=sim,
objective_functions=[J],
objective_arguments=ob_list,
design_regions=[design_region],
frequencies=frequencies,
decay_by=1e-5,
)
f0, dJ_du = opt()
db = 1e-5
choose = 1000
g_discrete, idx = opt.calculate_fd_gradient(num_gradients=choose, db=db)
(m, b) = np.polyfit(np.squeeze(g_discrete), dJ_du[idx], 1)
min_g = np.min(g_discrete)
max_g = np.max(g_discrete)
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot([min_g, max_g], [min_g, max_g], label="y=x comparison")
plt.plot([min_g, max_g], [m * min_g + b, m * max_g + b], "--", label="Best fit")
plt.plot(g_discrete, dJ_du[idx], "o", label="Adjoint comparison")
plt.xlabel("Finite Difference Gradient")
plt.ylabel("Adjoint Gradient")
plt.legend()
plt.grid(True)
plt.axis("square")
plt.subplot(1, 2, 2)
rel_err = (
np.abs(np.squeeze(g_discrete) - np.squeeze(dJ_du[idx]))
/ np.abs(np.squeeze(g_discrete))
* 100
)
plt.semilogy(g_discrete, rel_err, "o")
plt.grid(True)
plt.xlabel("Finite Difference Gradient")
plt.ylabel("Relative Error (%)")
plt.show()
plt.savefig("graph.png")
plt.cla()
plt.clf()
plt.close()
plt.show()Checked comment and issue list before upload this issue.
|


edit (1/11): updated script with suggestion to disable subpixel smoothing in
MaterialGrid(on by default) from @smartalecH which significantly improves accuracy.This is an initial attempt to verify the accuracy of the adjoint gradients in 3D. Once we are able to get this example working, we can consider converting it into a unit test for #2661 as well as a tutorial example.
The example involves a power splitter (shown in the schematic below) at$\lambda$ = 1.55 μm for a silicon waveguide on a silicon dioxide substrate. This particular SOI waveguide is identical to an existing tutorial with the schematic and band diagram also shown below. The nice thing about the power splitter is that it is an extension of a similar example in 2D and can be modified to use various types of objective arguments ($z$ direction. The example uses either a constant or random design region. The entire simulation runs in about 25 minutes using 3 Xeon 4.2 GHz cores.
EigenmodeCoefficient,FourierFields,LDOS) and a broad bandwidth objective function. The design region is a 2D grid with the pixels extruded in theThe test involves the usual comparison of the directional derivative computed using (1) a brute-force finite difference and (2) the adjoint gradient. (This calculation is similar to the 2D simulation of a 1D grating in #2054 (comment).) The MPB output of the simulation shows that the correct waveguide mode is being computed (i.e., matching the values for ($k$ , $\omega$ ) at the red dot in the band diagram below).
At a resolution of 20 pixels/μm, there is a large discrepancy in the finite-difference and adjoint-gradient results:
This discrepancy does not seem to decrease with increasing resolution. @smartalecH, any thoughts?
The text was updated successfully, but these errors were encountered: