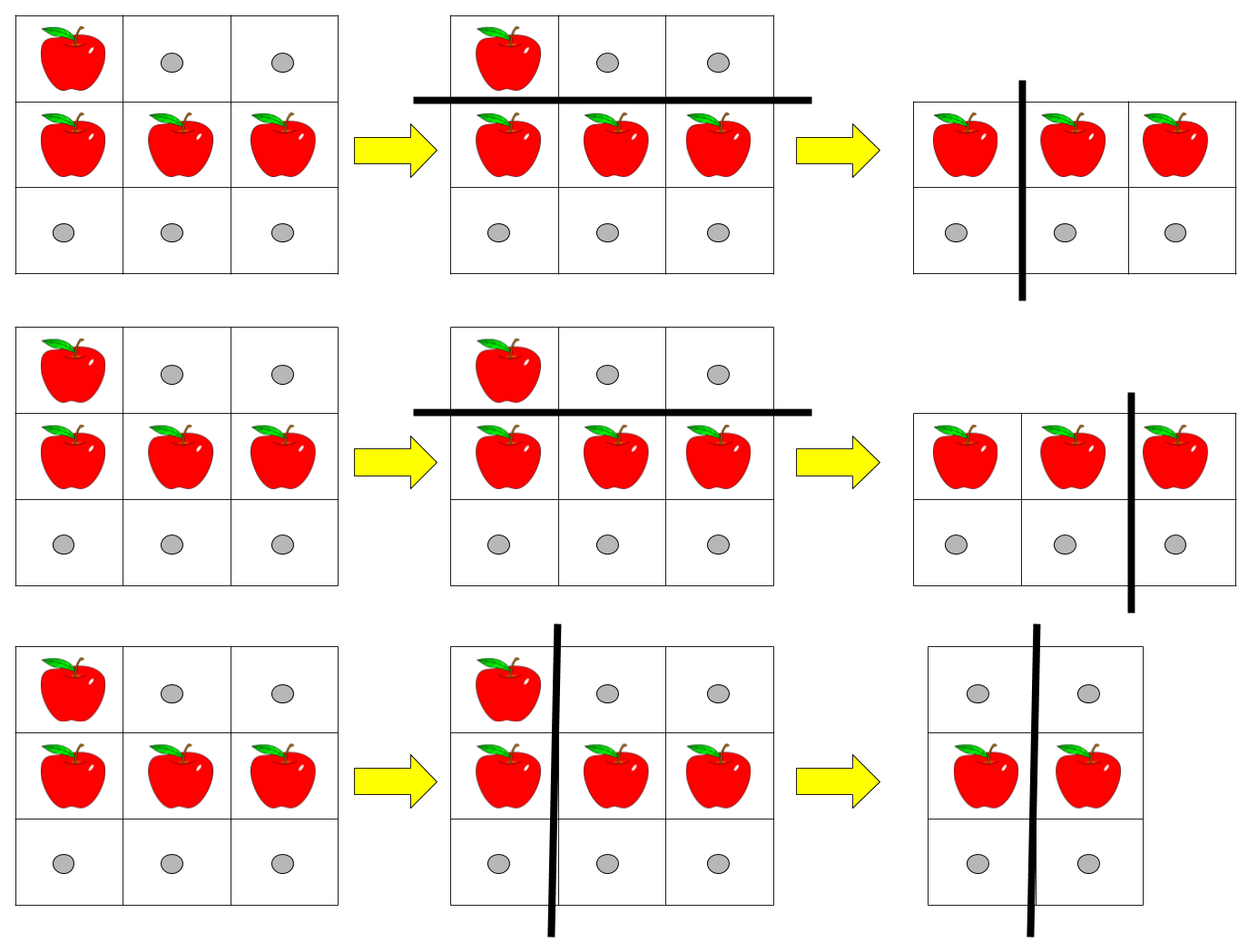
给你一个 rows x cols 大小的矩形披萨和一个整数 k ,矩形包含两种字符: 'A' (表示苹果)和 '.' (表示空白格子)。你需要切披萨 k-1 次,得到 k 块披萨并送给别人。
切披萨的每一刀,先要选择是向垂直还是水平方向切,再在矩形的边界上选一个切的位置,将披萨一分为二。如果垂直地切披萨,那么需要把左边的部分送给一个人,如果水平地切,那么需要把上面的部分送给一个人。在切完最后一刀后,需要把剩下来的一块送给最后一个人。
请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字,请你返回它对 10^9 + 7 取余的结果。
示例 1:
输入:pizza = ["A..","AAA","..."], k = 3 输出:3 解释:上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。
示例 2:
输入:pizza = ["A..","AA.","..."], k = 3 输出:1
示例 3:
输入:pizza = ["A..","A..","..."], k = 1 输出:1
提示:
1 <= rows, cols <= 50rows == pizza.lengthcols == pizza[i].length1 <= k <= 10pizza只包含字符'A'和'.'。
方法一:二维前缀和 + 记忆化搜索
我们可以使用二维前缀和来快速计算出每个子矩形中苹果的数量,定义
其中
接下来,我们设计一个函数
- 如果
$k = 0$ ,表示没有刀可以切了,那么我们需要判断矩形中是否有苹果,如果有苹果,则返回$1$ ,否则返回$0$ ; - 如果
$k \gt 0$ ,我们需要枚举最后一刀的切法,如果最后一刀是水平切,那么我们需要枚举切的位置$x$ ,其中$i \lt x \lt m$ ,如果$s[x][n] - s[i][n] - s[x][j] + s[i][j] \gt 0$ ,说明切出来的上面一块披萨中有苹果,我们累加$dfs(x, j, k-1)$ 的值到答案中;如果最后一刀是垂直切,那么我们需要枚举切的位置$y$ ,其中$j \lt y \lt n$ ,如果$s[m][y] - s[i][y] - s[m][j] + s[i][j] \gt 0$ ,说明切出来的左边一块披萨中有苹果,我们累加$dfs(i, y, k-1)$ 的值到答案中。
最终的答案即为
为了避免重复计算,我们可以使用记忆化搜索的方法,用一个三维数组
时间复杂度
相似题目:2312. 卖木头块
class Solution:
def ways(self, pizza: List[str], k: int) -> int:
@cache
def dfs(i: int, j: int, k: int) -> int:
if k == 0:
return int(s[m][n] - s[i][n] - s[m][j] + s[i][j] > 0)
ans = 0
for x in range(i + 1, m):
if s[x][n] - s[i][n] - s[x][j] + s[i][j] > 0:
ans += dfs(x, j, k - 1)
for y in range(j + 1, n):
if s[m][y] - s[i][y] - s[m][j] + s[i][j] > 0:
ans += dfs(i, y, k - 1)
return ans % mod
mod = 10**9 + 7
m, n = len(pizza), len(pizza[0])
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(pizza, 1):
for j, c in enumerate(row, 1):
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + int(c == 'A')
return dfs(0, 0, k - 1)class Solution {
private int m;
private int n;
private int[][] s;
private Integer[][][] f;
private final int mod = (int) 1e9 + 7;
public int ways(String[] pizza, int k) {
m = pizza.length;
n = pizza[0].length();
s = new int[m + 1][n + 1];
f = new Integer[m][n][k];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
int x = pizza[i - 1].charAt(j - 1) == 'A' ? 1 : 0;
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x;
}
}
return dfs(0, 0, k - 1);
}
private int dfs(int i, int j, int k) {
if (k == 0) {
return s[m][n] - s[i][n] - s[m][j] + s[i][j] > 0 ? 1 : 0;
}
if (f[i][j][k] != null) {
return f[i][j][k];
}
int ans = 0;
for (int x = i + 1; x < m; ++x) {
if (s[x][n] - s[i][n] - s[x][j] + s[i][j] > 0) {
ans = (ans + dfs(x, j, k - 1)) % mod;
}
}
for (int y = j + 1; y < n; ++y) {
if (s[m][y] - s[i][y] - s[m][j] + s[i][j] > 0) {
ans = (ans + dfs(i, y, k - 1)) % mod;
}
}
return f[i][j][k] = ans;
}
}class Solution {
public:
int ways(vector<string>& pizza, int k) {
const int mod = 1e9 + 7;
int m = pizza.size(), n = pizza[0].size();
vector<vector<vector<int>>> f(m, vector<vector<int>>(n, vector<int>(k, -1)));
vector<vector<int>> s(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
int x = pizza[i - 1][j - 1] == 'A' ? 1 : 0;
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x;
}
}
function<int(int, int, int)> dfs = [&](int i, int j, int k) -> int {
if (k == 0) {
return s[m][n] - s[i][n] - s[m][j] + s[i][j] > 0 ? 1 : 0;
}
if (f[i][j][k] != -1) {
return f[i][j][k];
}
int ans = 0;
for (int x = i + 1; x < m; ++x) {
if (s[x][n] - s[i][n] - s[x][j] + s[i][j] > 0) {
ans = (ans + dfs(x, j, k - 1)) % mod;
}
}
for (int y = j + 1; y < n; ++y) {
if (s[m][y] - s[i][y] - s[m][j] + s[i][j] > 0) {
ans = (ans + dfs(i, y, k - 1)) % mod;
}
}
return f[i][j][k] = ans;
};
return dfs(0, 0, k - 1);
}
};func ways(pizza []string, k int) int {
const mod = 1e9 + 7
m, n := len(pizza), len(pizza[0])
f := make([][][]int, m)
s := make([][]int, m+1)
for i := range f {
f[i] = make([][]int, n)
for j := range f[i] {
f[i][j] = make([]int, k)
for h := range f[i][j] {
f[i][j][h] = -1
}
}
}
for i := range s {
s[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1]
if pizza[i-1][j-1] == 'A' {
s[i][j]++
}
}
}
var dfs func(i, j, k int) int
dfs = func(i, j, k int) int {
if f[i][j][k] != -1 {
return f[i][j][k]
}
if k == 0 {
if s[m][n]-s[m][j]-s[i][n]+s[i][j] > 0 {
return 1
}
return 0
}
ans := 0
for x := i + 1; x < m; x++ {
if s[x][n]-s[x][j]-s[i][n]+s[i][j] > 0 {
ans = (ans + dfs(x, j, k-1)) % mod
}
}
for y := j + 1; y < n; y++ {
if s[m][y]-s[m][j]-s[i][y]+s[i][j] > 0 {
ans = (ans + dfs(i, y, k-1)) % mod
}
}
f[i][j][k] = ans
return ans
}
return dfs(0, 0, k-1)
}function ways(pizza: string[], k: number): number {
const mod = 1e9 + 7;
const m = pizza.length;
const n = pizza[0].length;
const f = new Array(m)
.fill(0)
.map(() => new Array(n).fill(0).map(() => new Array(k).fill(-1)));
const s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
for (let i = 1; i <= m; ++i) {
for (let j = 1; j <= n; ++j) {
const x = pizza[i - 1][j - 1] === 'A' ? 1 : 0;
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x;
}
}
const dfs = (i: number, j: number, k: number): number => {
if (f[i][j][k] !== -1) {
return f[i][j][k];
}
if (k === 0) {
return s[m][n] - s[i][n] - s[m][j] + s[i][j] > 0 ? 1 : 0;
}
let ans = 0;
for (let x = i + 1; x < m; ++x) {
if (s[x][n] - s[i][n] - s[x][j] + s[i][j] > 0) {
ans = (ans + dfs(x, j, k - 1)) % mod;
}
}
for (let y = j + 1; y < n; ++y) {
if (s[m][y] - s[i][y] - s[m][j] + s[i][j] > 0) {
ans = (ans + dfs(i, y, k - 1)) % mod;
}
}
return (f[i][j][k] = ans);
};
return dfs(0, 0, k - 1);
}