-
Notifications
You must be signed in to change notification settings - Fork 0
Home
Welcome to the TerrestrialGravitation wiki!
Here is the text of the paper:
Copyright © 2018 Raymond Arias, Jr. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation License".
(Please see GFDL under GFDL.md in Code section.)
I Need to Make a 2D Simulation, Game, or Other Software, and I Need to Account for Gravity! What Do I Do?
Calm down. It’s not a problem. You just need to learn (or brush up on) your terrestrial kinematics. This is a basic Newtonian (as opposed to Relativistic or Quantum and all that fancy newer stuff) description of how gravity and motion work here on Earth (as opposed to in space and stuff). Terrestrial kinematics entails horizontal kinematics, which as you may guess is a description of horizontal motion, and vertical kinematics, description of vertical motion. Here is each one in detail. If you don’t know calculus, don’t let it scare you. I just put it there for those who can read it.
Since any forces pushing or pulling upon any object in the horizontal while it is flying through the air are negligible. (There is friction, both static and kinetic, with gaseous air particles, but it is very small for most objects, except when dealing with winds of great velocity, as in tornados and hurricanes, or taking into account objects that can be greatly affected by wind resistance or can take advantage of aerodynamic lift, such as gliders, airplanes, and parachutes. By the way, the physics of wind resistance and aerodynamic life are extremely complicated and are not covered in this short supplemental paper.) Therefore, a solid object being thrown, catapulted, or otherwise projected into the air, can generally be considered as having neither any thrust added to, nor any resistance taken away from, its initial motion. Hence, the horizontal speed is practically constant; there is no horizontal component of acceleration to take into account. Consequently, the horizontal position only changes by adding the same constant quantity to the previous position when animating in 2D software.
a_x (t)=0 a_(x ) (t)=(dv_x)/dt ∫_0^t▒a_(x ) (t) dt=∫_0^t▒〖(dv_x)/dt dt〗 v_x (t)=v_x (0) v_x (t)=dx/dt ∫_0^t▒v_x (t)dt=∫_0^t▒dx/dt dt x(t)=x(0)+ v_x (t)t
As with horizontal kinematics, the mechanics of vertical motion of objects through the air, though continuously affected by the friction of gaseous air particles, this friction is so small that in most circumstances that it can be neglected, again, except in cases where it becomes so large, such as in gliders, airplanes, parachutes, etc. With this in mind, the vertical motion of objects flying through the air, for instance after being catapulted or thrown, is similar to that of an object loaded on top of a coiled spring and then propelled by allowing the spring to uncoil. This object would then be shot upward by the force of the uncoiling spring. This upward force would immediately be counteracted by the downward force of terrestrial gravity. Once the object is out of contact with the spring, the object would continue upward with whatever velocity was given to it by the force of the spring. This upward velocity would reduce until it reaches zero as gravitation would be the only force affecting the object after that point. Additionally, after reaching its vertex (the highest point in its vertical path), the object would then gain a downward velocity from the continued gravitation affecting it. This velocity would be small at first and then grow to its maximum just before the object either reloads the spring, recoiling it in the process, or hits the ground. Generally, a vertically propelled object returns with a downward velocity of the same magnitude, at the same height that it started, as the initial upward velocity that it was originally driven to by the upward force of the spring. For example, if a ball was thrown straight up at 10 miles/hour, by the time it finishes going up, gets to it vertex, and goes down, when it reaches the same height it was thrown up at, it should be going straight down at pretty much (if not exactly) 10 mi/hr.
After this point, if an object with downward velocity is allowed to make contact with the ground, depending upon what the ground is made of and what the object is made of, the object will bounce back up at some fractional upward velocity of the downward velocity it came down with. For a rubber ball on a hard surface, this fraction is very large, for a less bouncy object on a plush surface, this fraction is very small. This fraction is known as the coefficient of restitution (CoR). However, other than touching on it briefly here, I will not cover CoR any further in this paper.
The terrestrial force of gravity upon any object’s mass is G⊕, which is equal to mg, the mass of the object (m) multiplied by the acceleration given to it by the gravitation between the object and the Earth (g). This acceleration is expressed either in US Customary Units as 32.1740 feet/sec2 or in the International System of Units (SI) as 9.80665 meters/sec2. These are averages and actual measurements for g can vary according to altitude from sea level.
G_⊕ =mg a_y (t)=g (g=9.8 m/sec^2 ,g=32ft/sec^2 ) a_(y ) (t)=g (dv_y)/dt ∫_0^t▒a_(y ) (t) dt=g∫_0^t▒〖(dv_y)/dt dt〗 v_y (t)=〖g v〗_y (0) v_y (t)=g dy/dt ∫_0^t▒v_y (t)dt=g∫_0^t▒dy/dt dt y(t)=y(0)+ v_y (0)+1/2 gt^2
If these facts are applied separately to each of the axes, when plotted on a graph using sample initial velocities for each direction, the following is obtained:
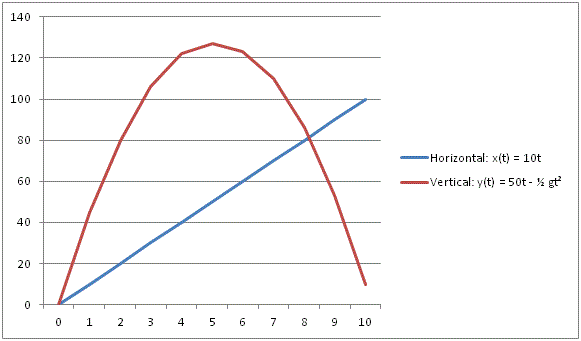
If both axes are applied jointly, this graph is obtained:
Well, I understand many people reading this may not even know calculus. (I just thought I’d throw the calculus in for those who do understand it.) But basically, this is going to all break down like this. Since on the horizontal axis, the velocity is going to be constant, you can assign a constant velocity
vx = 10;
x = x + vx;
or neglect it entirely as you can just hard code the constant directly when you are changing the x-coordinate.
x = x + 10;
For the vertical velocity, you will need a variable though. It is your choice, however, if you want to keep a constant--such as,
g = 9.8;
vy = vy – g;
y = y + vy;
or hard code when you change your vertical velocity.
vy = vy – 9.8;
y = y + vy;
Nevertheless, keep in mind that 9.8 (m/s)/s—or whichever number you select for g—is a change that occurs every whole second, so if you are changing your vertical velocity 100 times per second, you will need to divide this number by 100. Thus, you should use either something like
g = 9.8;
vy = vy – (g / 100);
or,
g100 = 0.98;
vy = vy – g100;
or even,
g = 9.8;
dt = 100;
vy = vy – (g / dt);
Whichever works for you, when your object finally flies across the screen, you should get a similar shape to the second graph (concave down parabola). If not, you need to double check your math. Good luck!