Skip to content

Latest commit

 

History

History
61 lines (46 loc) · 2.15 KB

README.md

File metadata and controls

61 lines (46 loc) · 2.15 KB
Raw

non-normal

Generate a non-normal distributions with given a mean, variance, skewness and kurtosis using the Fleishman Method, essentially a cubic transformation on a standard normal [X~N(0, 1)]

$$ Y =a +bX +cX^2 +dX^3 $$

where the coefficients ($a, b, c, d$) are tuned to create a distribution with the desired statistic

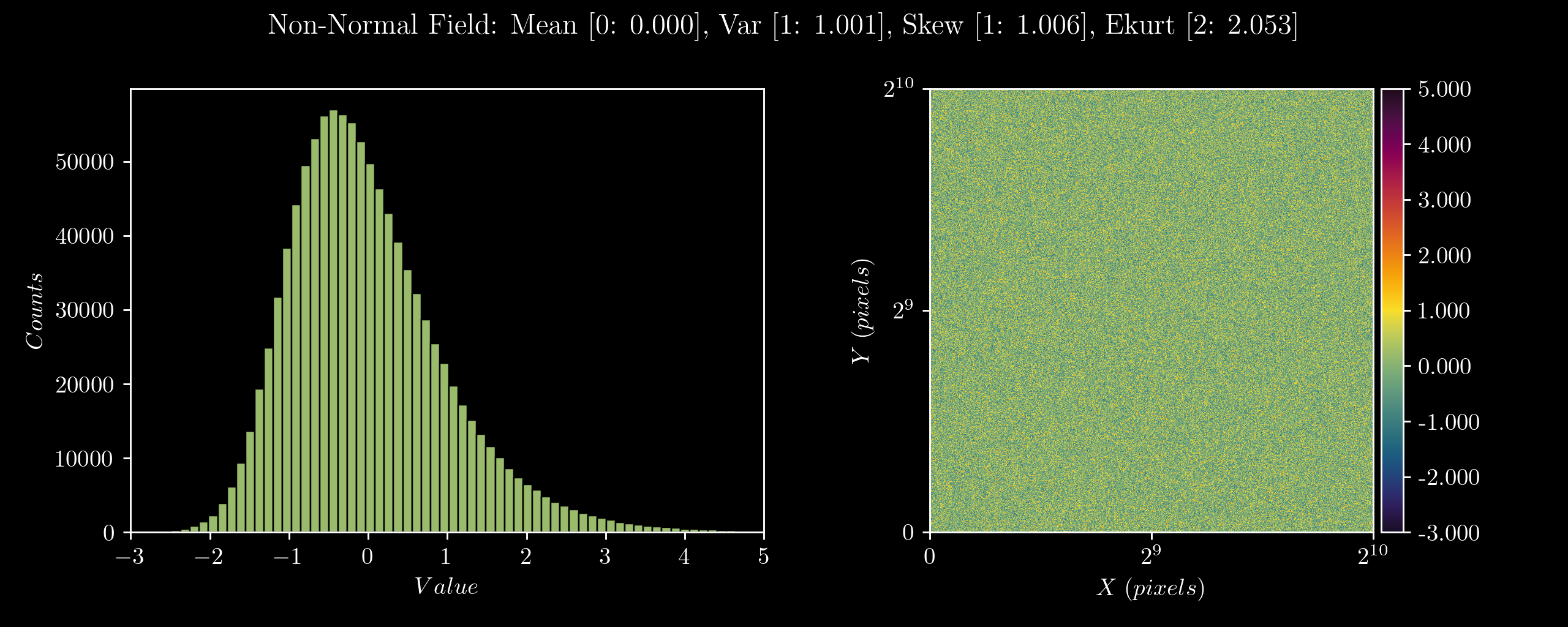Non-Normal Distribution Figure 1. A non-normal field generated in the usage section below. The title shows the input parameters, and the emperically measured statistics of the generated distribution

Installation

Installs cleanly with a single invocation of the standard Python package tool:

$ pip install non-normal

Usage

from non_normal import fleishman

# Input parameters for non-normal field
mean = 0
var = 1
skew = 1
ekurt = 2
size = 2**20

# Create an instance of the Fleishman class
ff = fleishman.Fleishman(mean=mean, var=var, skew=skew, ekurt=ekurt, size=size)

# Generate the field
ff.gen_field()
non_normal_data = ff.field

# Measure the stats of the generated samples
ff.field_stats

>>> {'mean':    0.000203128504124, 
     'var':     1.001352686678266, 
     'skew':    1.005612915524984, 
     'ekurt':   2.052527629375554,}

References

  1. A method for simulating non-normal distributions
  2. Functions for Simulating Data by Using Fleishman’s Transformation
  3. Generation of Non-normal Data – A Study of Fleishman’s Power Method
  4. Computing the real solutions of Fleishman's equations for simulating non-normal data
  5. Simulating multivariate nonnormal distributions
  6. https://gist.github.com/zeimusu/7432603b85dc6406c6ea