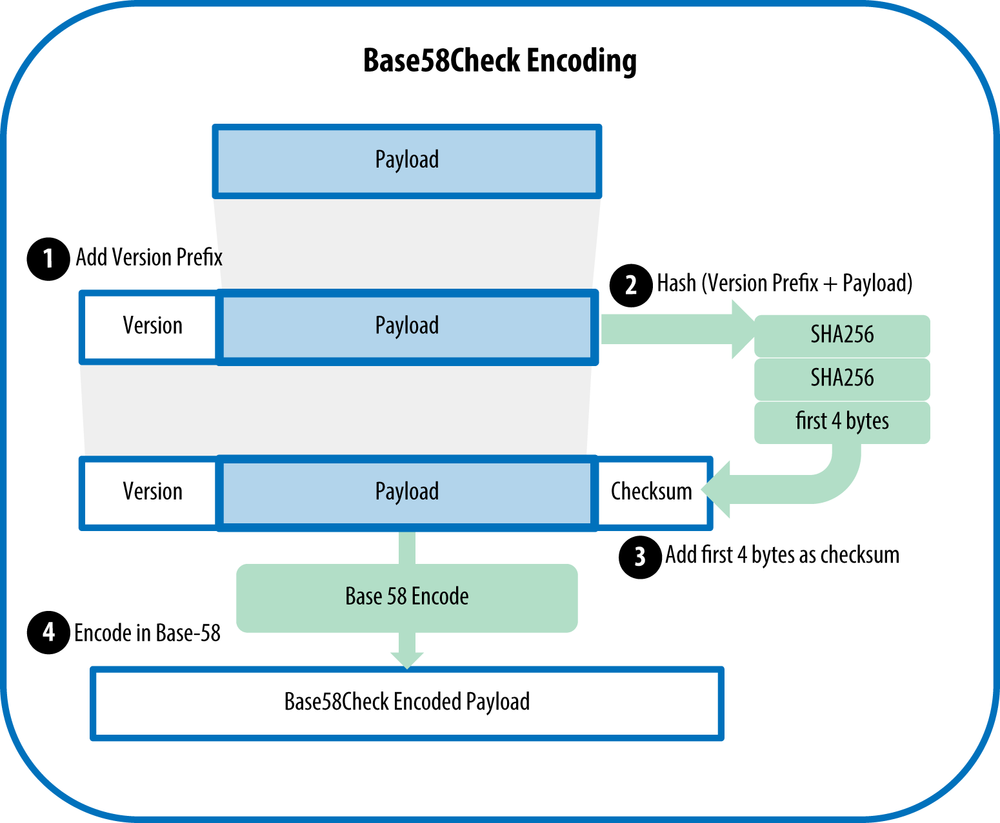
an introduction to the Bitcoin (BTC) network and how addresses are made
It has come to my attention that a Security comment was made regarding the microlect repository, claiming that it contains a malicious binary folder. I want to assure all users that these claims are entirely false.
The microlect file is not a runnable executable but rather an obfuscated script intended as a deobfuscation challenge. For transparency and to alleviate any concerns, I have scanned the repository files using multiple antivirus tools, including VirusTotal. The scans confirm that there is no malicious code or malware present in the repository.
You can review the VirusTotal scan results here: VirusTotal Scan Report
- This project is no longer under active development or maintenance. It now serves as a concise document providing an introduction to the Bitcoin (BTC) network and explaining the process of how Bitcoin addresses are created.
BTC gone? Better to learn and move on! (The chances of recovering your wallet are about as likely as pigs flying!)
The decrypted file will reveal the source code with instructions on how to use it.
Happy hacking!
btc wallet attack.
Just in case for learn about how bitcoin network working.
And learn the Math behind The running service.
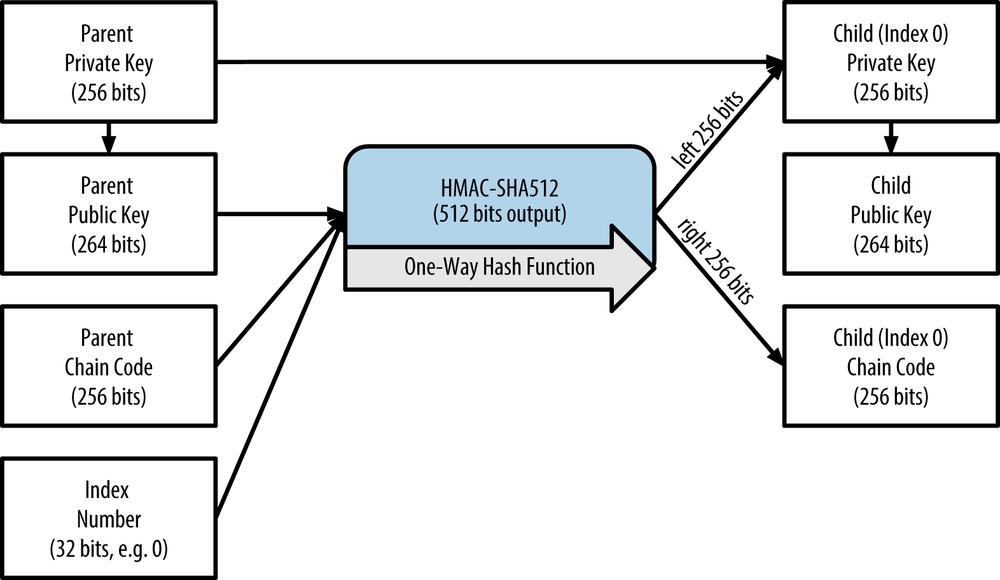
A bitcoin wallet contains a collection of key pairs, each consisting of a private key and a public key. The private key (k) is a number, usually picked at random. From the private key, we use elliptic curve multiplication, a one-way cryptographic function, to generate a public key (K). From the public key (K), we use a one-way cryptographic hash function to generate a bitcoin address (A). In this section, we will start with generating the private key, look at the elliptic curve math that is used to turn that into a public key, and finally, generate a bitcoin address from the public key. The relationship between private key, public key, and bitcoin address is shown in Figure:

A private key is simply a number, picked at random. Ownership and control over the private key is the root of user control over all funds associated with the corresponding bitcoin address. The private key is used to create signatures that are required to spend bitcoins by proving ownership of funds used in a transaction. The private key must remain secret at all times, because revealing it to third parties is equivalent to giving them control over the bitcoins secured by that key. The private key must also be backed up and protected from accidental loss, because if it’s lost it cannot be recovered and the funds secured by it are forever lost. While cracking Bitcoin wallets is technically possible in theory, it is extremely hard, time-consuming, and has an extraordinarily low chance of success due to the robust cryptographic systems in place. Attempting to do so without proper authorization is also illegal and unethical.
It is important to use technology responsibly and ethically at all times.
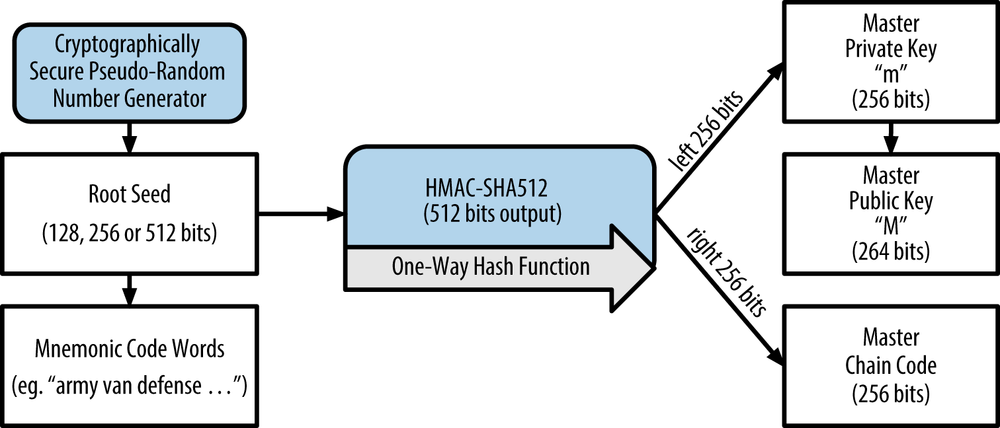
The first and most important step in generating keys is to find a secure source of entropy, or randomness. Creating a bitcoin key is essentially the same as “Pick a number between 1 and 2^256.” The exact method you use to pick that number does not matter as long as it is not predictable or repeatable. Bitcoin software uses the underlying operating system’s random number generators to produce 256 bits of entropy (randomness). Usually, the OS random number generator is initialized by a human source of randomness, which is why you may be asked to wiggle your mouse around for a few seconds. For the truly paranoid, nothing beats dice, pencil, and paper.
More accurately, the private key can be any number between 1 and n - 1, where n is a constant (n = 1.158 * 10^77, slightly less than 2^256 defined as the order of the elliptic curve used in bitcoin. To create such a key, we randomly pick a 256-bit number and check that it is less than n - 1. In programming terms, this is usually achieved by feeding a larger string of random bits, collected from a cryptographically secure source of randomness, into the SHA256 hash algorithm that will conveniently produce a 256-bit number. If the result is less than n - 1, we have a suitable private key. Otherwise, we simply try again with another random number.
The following is a randomly generated private key (k) shown in hexadecimal format (256 binary digits shown as 64 hexadecimal digits, each 4 bits):
''' 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD '''
The size of bitcoin’s private key space, 2^256 is an unfathomably large number. It is approximately 10^77 in decimal.
The public key is calculated from the private key using elliptic curve multiplication, which is irreversible: K=k*G where k is the private key, G is a constant point called the generator point and K is the resulting public key. The reverse operation, known as “finding the discrete logarithm”—calculating k if you know K—is as difficult as trying all possible values of k, i.e., a brute-force search. Before we demonstrate how to generate a public key from a private key, let’s look at elliptic curve cryptography in a bit more detail.
Elliptic curve cryptography is a type of asymmetric or public-key cryptography based on the discrete logarithm problem as expressed by addition and multiplication on the points of an elliptic curve.
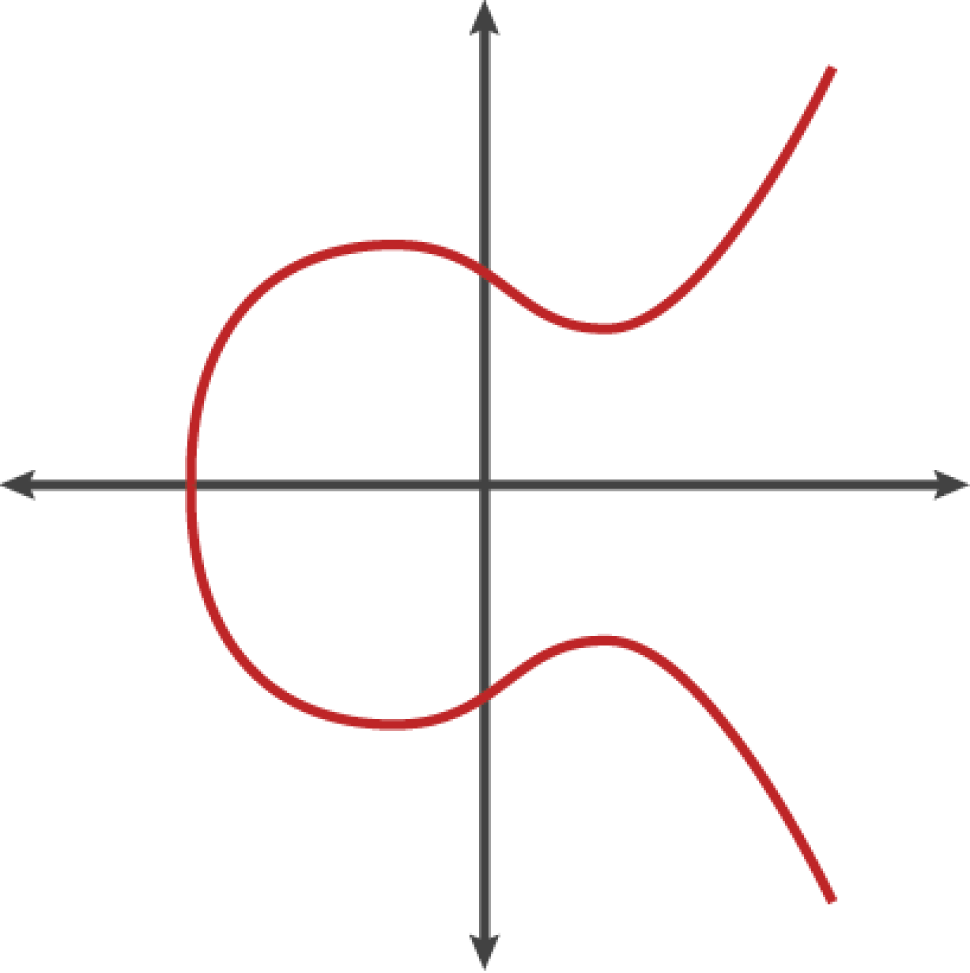
Bitcoin uses a specific elliptic curve and set of mathematical constants, as defined in a standard called secp256k1, established by the National Institute of Standards and Technology (NIST). The secp256k1 curve is defined by the following function, which produces an elliptic curve:

The mod p (modulo prime number p) indicates that this curve is over a finite field of prime order p, also written as F of p where p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1, a very large prime number.
Because this curve is defined over a finite field of prime order instead of over the real numbers, it looks like a pattern of dots scattered in two dimensions, which makes it difficult to visualize. However, the math is identical as that of an elliptic curve over the real numbers.
So, for example, the following is a point P with coordinates (x,y) that is a point on the secp256k1 curve. You can check this yourself using Python:
""" P = (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424) """ In elliptic curve math, there is a point called the “point at infinity,” which roughly corresponds to the role of 0 in addition. On computers, it’s sometimes represented by x = y = 0 (which doesn’t satisfy the elliptic curve equation, but it’s an easy separate case that can be checked).
There is also a + operator, called “addition,” which has some properties similar to the traditional addition of real numbers that grade school children learn. Given two points P1 and P2 on the elliptic curve, there is a third point P3 = P1 + P2, also on the elliptic curve.
Geometrically, this third point P3 is calculated by drawing a line between P1 and P2. This line will intersect the elliptic curve in exactly one additional place. Call this point P3' = (x, y). Then reflect in the x-axis to get P3 = (x, –y).
There are a couple of special cases that explain the need for the “point at infinity.” If P1 and P2 are the same point, the line “between” P1 and P2 should extend to be the tangent on the curve at this point P1. This tangent will intersect the curve in exactly one new point. You can use techniques from calculus to determine the slope of the tangent line. These techniques curiously work, even though we are restricting our interest to points on the curve with two integer coordinates!
In some cases (i.e., if P1 and P2 have the same x values but different y values), the tangent line will be exactly vertical, in which case P3 = “point at infinity.”
If P1 is the “point at infinity,” then the sum P1 + P2 = P2. Similary, if P2 is the point at infinity, then P1 + P2 = P1. This shows how the point at infinity plays the role of 0.
It turns out that + is associative, which means that (A+B)C = A(B+C). That means we can write A+B+C without parentheses without any ambiguity.
Now that we have defined addition, we can define multiplication in the standard way that extends addition. For a point P on the elliptic curve, if k is a whole number, then kP = P + P + P + … + P (k times). Note that k is sometimes confusingly called an “exponent” in this case.
| format|private key | |Hex|1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD| |WIF | 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
USE IT FOR WALLET RECOVERY! (More chance of meeting aliens tomorrow! HAHA)
If you would like to support me, donations are very welcome.
You can use Paypal to donate using your own credit card. The payment is processed by PayPal but you don't need to have a PayPal account or sign-up for one if you are paying by credit card.
You can also donate Bitcoin, Bitcoin Cash, Tron, Ethereum, Litecoin and etc ...

The code within this repository comes with no guarantee, the use of this code is your responsibility*. I take 'NO' responsibility and/or liability for how you choose to use any of the source code available here. By using any of the files available in this repository, you understand that you are AGREEING TO USE AT YOUR OWN RISK.