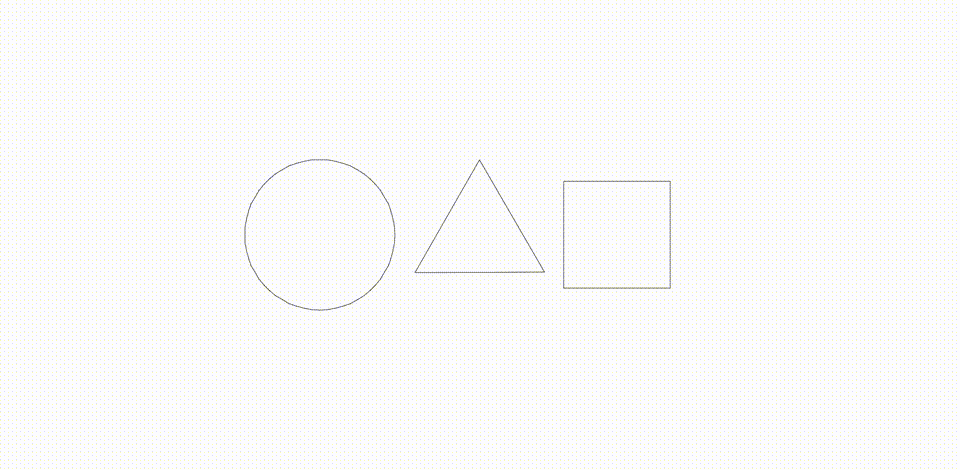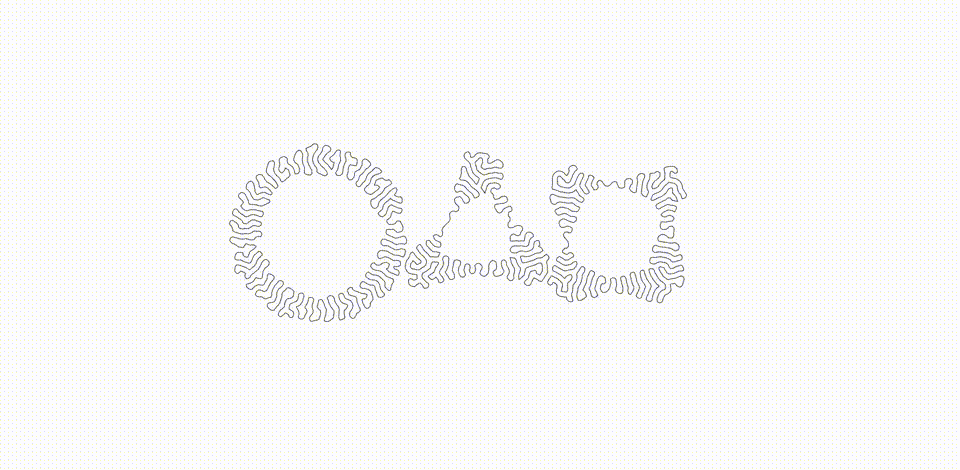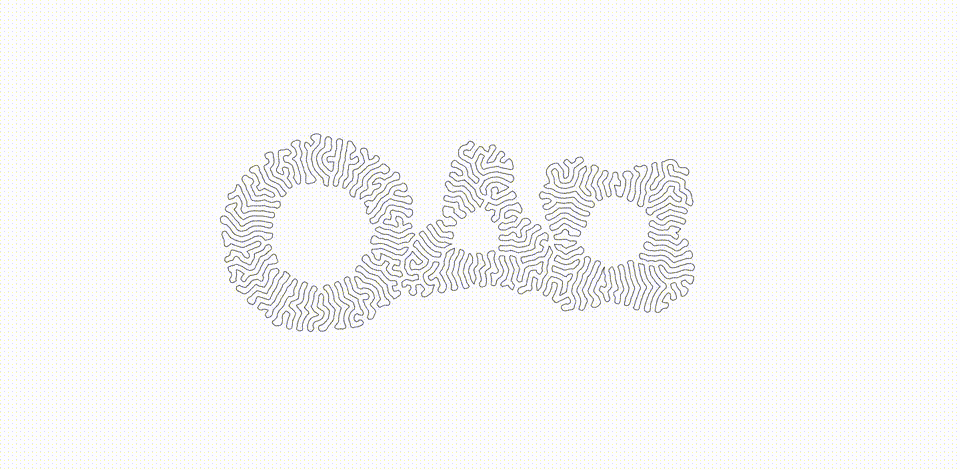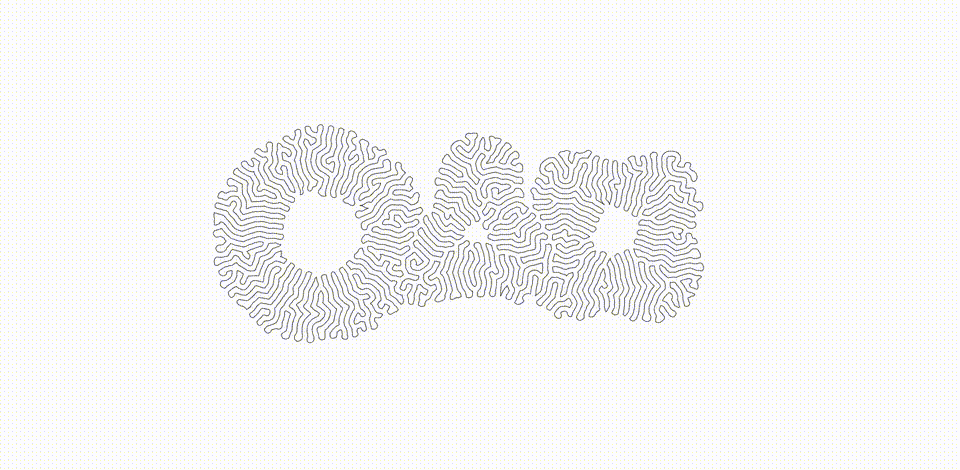Read my Medium article to learn more about differential growth and this project.
This repo contains a series of visual experiments built with JavaScript that explore the topic of differential growth as a method for generating interesting 2D forms.
I am particularly interested in the application of such techniques in the context of digital fabrication, so these experiments will be more focused on schematic representations (colorless, vector-based, SVG/STL exports) over purely visual effects.
Differential growth is a process that uses simple rules to produce undulating, buckling forms that mimic or simulate similar forms found in the natural world. Meandering rivers, rippled surface textures of plants/seeds/fruits, space-filling behaviors of worms, snakes, intestines, and more are all reminiscent of this process, perhaps even making use of some of the same principles through physical and organic components.
The process itself can be described algorithmically at a high level by first supposing that we are starting with a single continuous path consisting of points (called nodes) connected by lines (called edges). In such a system, we apply the following rules:
- Each node wants to be closer to it's connected neighbors, and will experience an attraction force towards them.
- Each node wants to sit on a straight line between it's neighbors to minimize curvature.
- Each node must never be too close to any other node to prevent pinching or breaking of the overall continuity of the line.
- When the distance between two nodes exceeds a predefined distance (due to the influence of the other rules), a new node must be injected between them to split the line.
- New nodes are introduced to the system according to some growth scheme in order to induce asymmetry.
- Without this rule the entire system would just uniformly expand and reach an equilibrium state.
Within these rules you can see several opportunities for customization that enable a certain amount of creative direction to be imposed by the developer. These include:
- The maximum distance between connected nodes before their shared edge is split.
- The minimum distance between all nodes.
- The attraction force between connected nodes.
- The repulsion force between nearby nodes.
- The radius around each node used to calculate which nearby nodes have an influence on it.
- A growth scheme that determines when and how new nodes are introduced to the system to induce interesting asymmetry.
All of these keyboard controls are available in each experiment.
| Key | Result |
|---|---|
1-9 |
Change initial seed path shape (if available) |
t |
Toggle trace mode |
n |
Toggle visibility of nodes |
r |
Reset simulation with same parameters |
Space |
Pause or unpause the simulation |
i |
Toggle inverting of colors |
d |
Toggle "debug mode" |
f |
Toggle shape fills |
h |
Toggle drawing of periodic path history |
s |
Download an SVG of current geometry |
b |
Toggle visibility of path bounds |
This repository is more like a sketchbook, meant to contain some thematic scribbles on the topic of differential growth. I did not take a very rigorous approach in these experiments, opting to focus more on curiosity and effects than sheer performance and broader applications.
There are a lot of ways that the code I've written can be improved, or the algorithm itself explored more deeply, and I encourage you to take the next steps to expand upon what I've provided and create something new and awesome! Here are a few ideas that I've thought about exploring:
- Tune forces (attraction, repulsion, and alignment) to identify stable and interesting regions of the parameter space.
- Make optimization improvements to enable larger scales, without compromising too much in code readability.
- Maybe a more efficient spatial index or nearest-neighbor algorithm can be found?
- Move into the third dimension. Many routes to explore here, including:
- Keep the simulation focused on 2D, but take snapshots on intervals and increment Z position for next iteration.
- Use a 3D package like ThreeJS and map the same 2D simulation onto the surfaces of 3D meshes.
- Explore professional-grade VFX and CAD options like Houdini, Unity, and Rhino + Grasshopper to achieve extreme performance.
- Port the code into a more performant language / framework like openFrameworks or Cinder. Even the Java-based Processing environment may show some performance gains!
- Differential line growth with Processing by Alberto Giachino (CodePlastic)
- Differential line by inconvergent
- Sheparding Random Growth by inconvergent
- Real-time differential growth in JavaScript by Adrian Toncean
- Differential Line Growth by Maritz Schwind of Entagma
- Differential Mesh Growth discussion thread on od|force forums
- Differential Growth by Lionel Radisson via CodePen
- Organic Labrynths and Mazes (PDF) paper by Hans Pederson and Karen Singh
- Run
npm installin both the root (/) andcore/folders. - Run
gulpto kick off a watch process and a browser window with LiveReload enabled. - Keep Gulp running and the browser window open while making changes. If all goes well, new builds will kick off when you save your changes and the browser will refresh!
- p5js for canvas drawing and miscellaneous helper functions (like
lerpandmap). - rbush for a fast R-tree spatial index implementation
- rbush-knn for k-nearest neighbors searching of rbush index
- point-in-polygon for constraining nodes inside of bounding paths
- svg-pathdata for extracting X,Y coordinates out of SVG
<path>elements. Used to import SVG files. - svg-points for generating the
dattribute of SVG<path>elements. Used to export SVG files from paths. - file-saver for initiating a download prompt when exporting SVG files
- browserify, babel, and others for working with modern ES6 and module patterns.