This package and repo tracks the constraints on the coupling and masses of heavy neutral leptons (HNL). To access it, simply clone this repository.
To use the underlying functions to create your own plots and latex files, you can install HNLimits as you would a standard PyPI package, python -m pip install HNLimits. You can then import it in your Python script import HNLimits.
All limits are kept track in this 
-
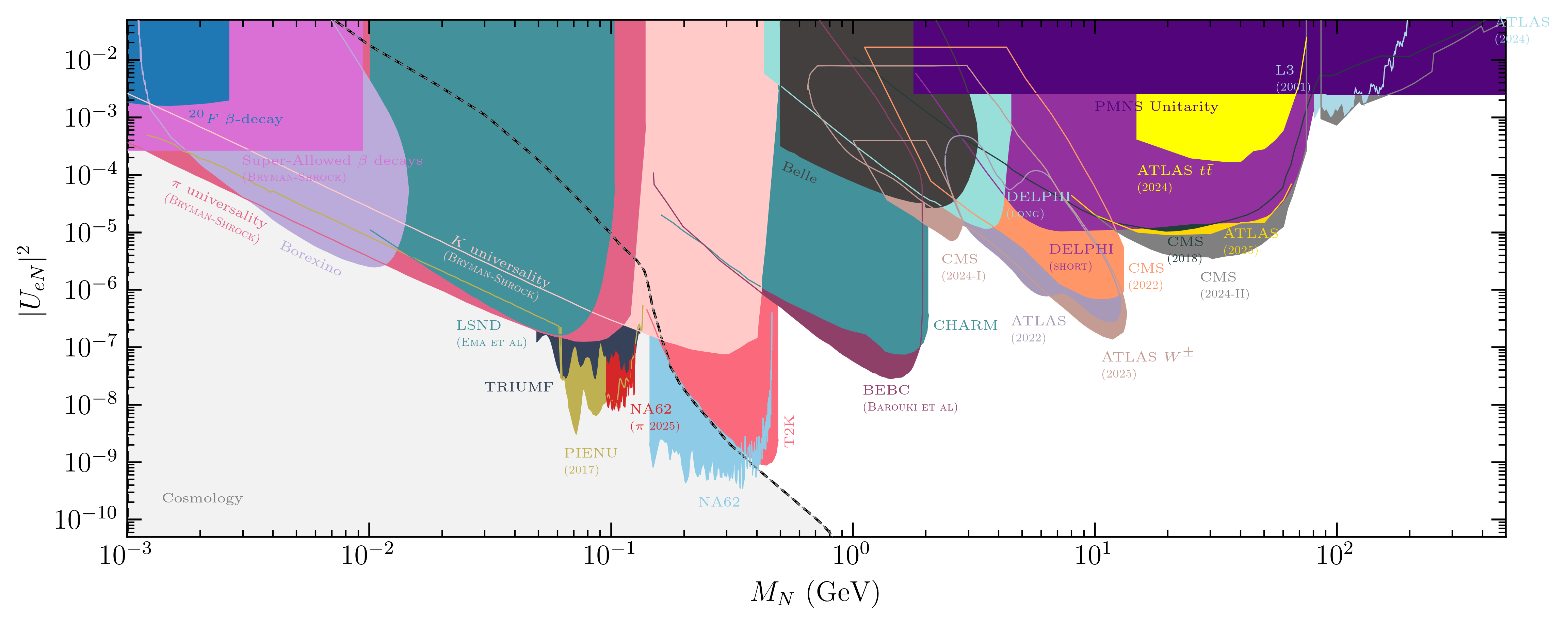
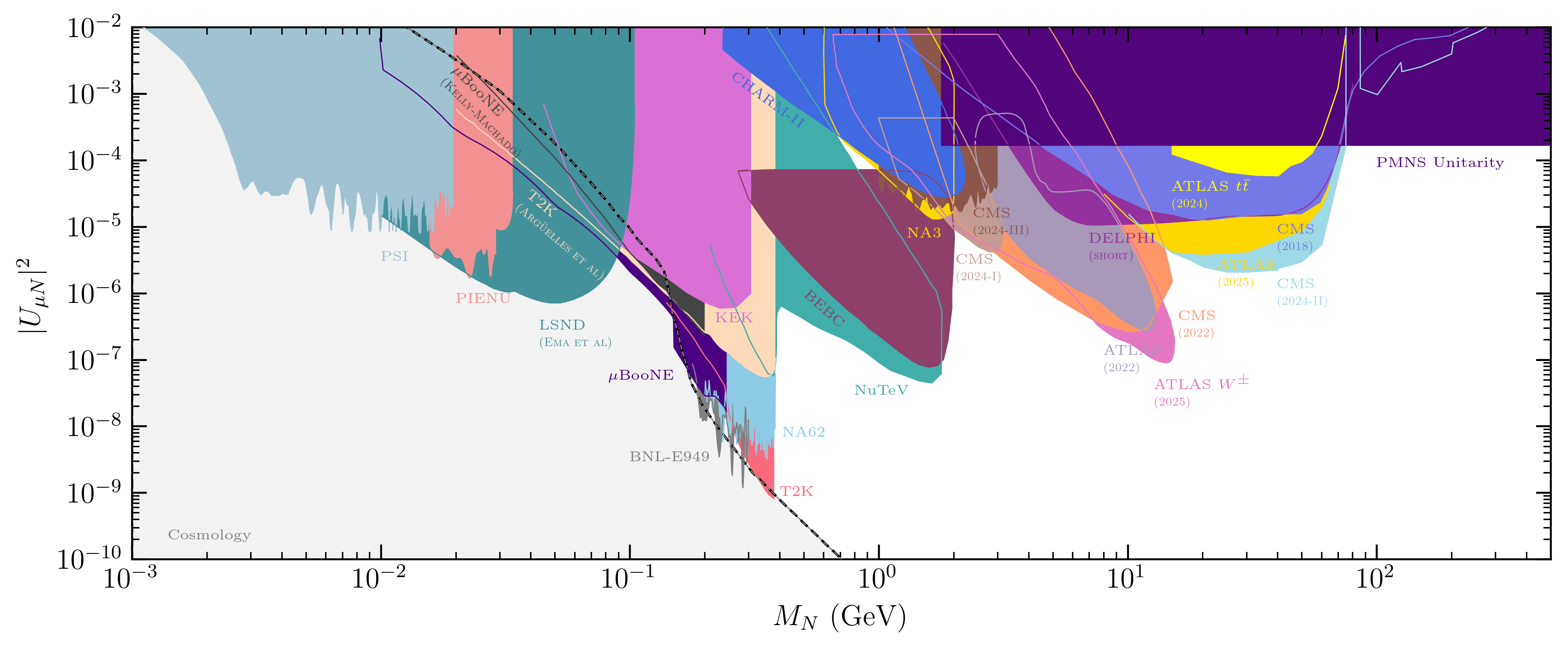
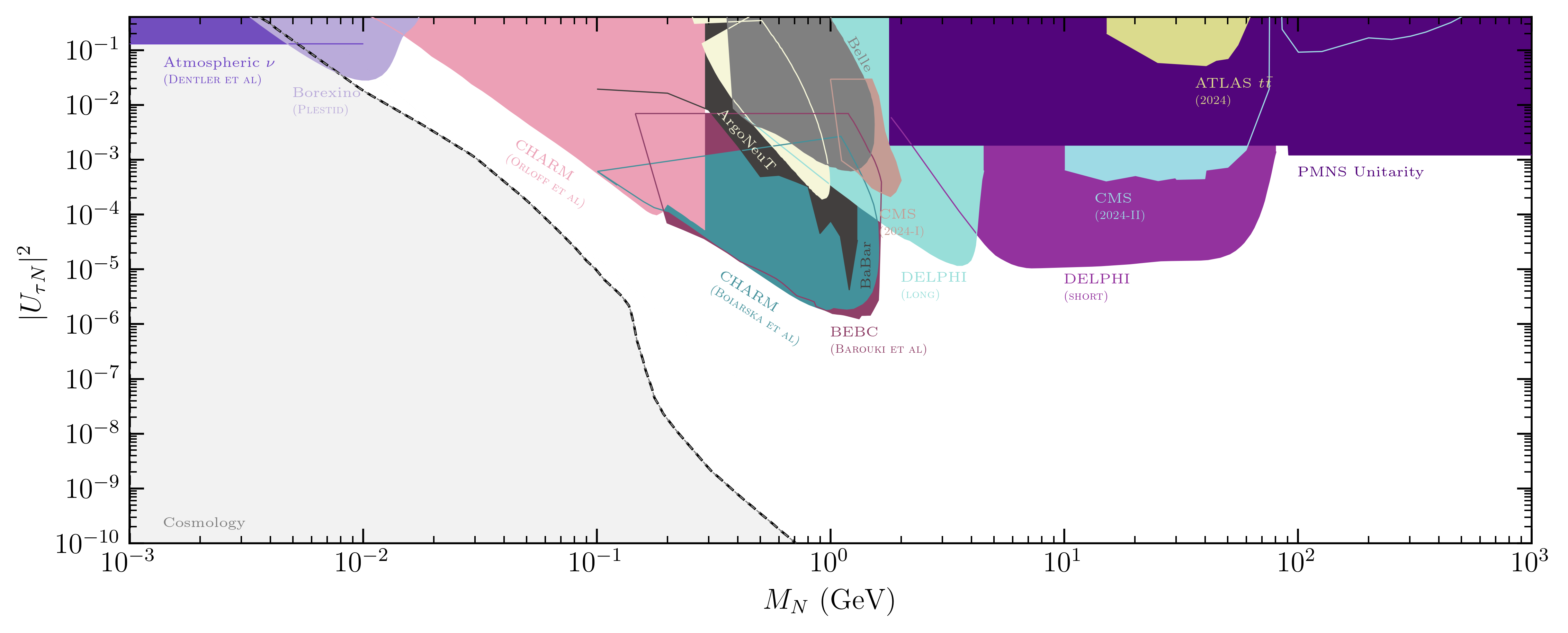
We consider single flavor dominance scenarios, where the HNL mixes predominantly with either the electron, muon, or tau flavor.
-
Following the accompanying paper, we provide limits on the Wilson coefficients of dimesnion-six
$\nu$ SMEFT operators as a function of the HNL mass$M_{N}$ . -
The code keeps track of limits in the region 1 MeV
$< M_{N} < 100$ GeV.
Additions, comments, or suggestions should be directed to:
- Josu Hernández-García ([email protected])
- Matheus Hostert ([email protected])
Citation info:
arxiv.org/abs/2304.06772
@article{Fernandez-Martinez:2023phj,
author = "Fern\'andez-Mart\'\i{}nez, Enrique and Gonz\'alez-L\'opez, Manuel and Hern\'andez-Garc\'\i{}a, Josu and Hostert, Matheus and L\'opez-Pav\'on, Jacobo",
title = "{Effective portals to heavy neutral leptons}",
eprint = "2304.06772",
archivePrefix = "arXiv",
primaryClass = "hep-ph",
reportNumber = "FTUV-23-0303.1224, IFIC/23-09",
doi = "10.1007/JHEP09(2023)001",
journal = "JHEP",
volume = "09",
pages = "001",
year = "2023"
}
Current compilation of bounds on the mixing of HNLs with a single flavor:
| Type | Name | Operator | Notebook | Figure |
|---|---|---|---|---|
| Mixing | 0_limits_mixing.ipynb |
electron muon tau |
||
| Higgs-dressed Mixing | 1_NSMEFT_LHN.ipynb |
electron muon tau |
||
| Bosonic Currents | 2_NSMEFT_bosonic_NC.ipynb |
Bosonic NC | ||
3_NSMEFT_bosonic_CC.ipynb |
Bosonic CC | |||
| Moments | 4_NSMEFT_moment_NB.ipynb |
Moment hypercharge | ||
5_NSMEFT_moment_NW.ipynb |
Moment W | |||
| 4-fermion NC | 6_NSMEFT_4fermion_NC_ff_LN.ipynb |
4-fermion ee 4-fermion uu 4-fermion dd |
||
6_NSMEFT_4fermion_NC_ff_LN.ipynb |
4-fermion LN | |||
7_NSMEFT_4fermion_NC_QN.ipynb |
4-fermion QN | |||
| 4-fermion NC & CC | 8_NSMEFT_4fermion_LNLell.ipynb |
4-fermion LNLell NC 4-fermion LNLell CC |
||
| 4-fermion CC | 9_NSMEFT_4fermion_CC_duNell.ipynb |
4-fermion duNell: electron 4-fermion duNell: muon 4-fermion duNell: tau |
||
10_NSMEFT_4fermion_CC_LNQd.ipynb |
4-fermion LNQd: electron 4-fermion LNQd: muon 4-fermion LNQd: tau |
|||
11_NSMEFT_4fermion_CC_QuNL.ipynb |
4-fermion QuNL: electron 4-fermion QuNL: muon 4-fermion QuNL: tau |