-
Notifications
You must be signed in to change notification settings - Fork 40
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
2D Wave Equation #30
Comments
|
@engsbk I would ask the same question here - what's your training horizon? The 1D Wave w/source actually look pretty good to me! Of course there's room for improvement but that is impressive for a first pass at it. |
|
The 2D case is tougher - that one may require some creativity. Try adding in self-adaptive weighting and see if that coaxes your residual errors to decrease a little better. There may also be an issue in the f_model definition but it looks reasonable to me, so that's just a guess. Weighting the IC a little heavier initially is usually a good starting point with SA weights. |
For the 2D problem, the loss had a low value, but the comparison results were not accurate. I'm not sure what do you mean by training horizon... |
|
Sure this can result from it finding the 0 solution, weighting the IC with SA weights should help. By training horizon I just mean the number of training iterations of Adam/BFGS. 20k is fine, in this case there's likely another issue with the 2D case. I bet if you dial down the adam learning rate and increase the number of training iterations on the 1D case you'll improve it. |
Good idea, I'll try changing the learning rate and IC weight and keep you posted with the results. Is there a tdq command for modifying the learning rate and weights instead of editing the env files? |
|
I just want to make sure Am I changing the IC weight using the correct lines: Also, I'm not sure how to change the learning rate, if you can help with this too, it'll be great. I've increased the collocation points just in case they're not enough. Please advise. |
|
This looks correct to me. Modification of the learning rate can be done by overwriting the default optimizer with another Adam optimizer with a different lr. See here for how to do so - https://tensordiffeq.io/hacks/optimizers/index.html |
Thanks! Before I read this page I just added I think what you referred to is a better generalization. Just In case other optimizers are to be tested. Changing Edit: Nevermind, I realized I can control that with Thank you for the informative documentation! |
|
I was trying to follow the example of self-adaptive training in https://tensordiffeq.io/model/sa-compiling-example/index.html, but I got this error: I'm not sure if I'm using an older version of Any suggestions on how to fix this? |
This is old syntax - sorry for the confusion. Your original script was correct, i.e. defining dict_adaptive. That was a recent change in syntax that needs updating still in some places in the documentation |
The only supported second order solver is L-BFGS, |
|
Hello @levimcclenny , Thanks for your suggestions. I avoided using SA because the loss kept increasing until |




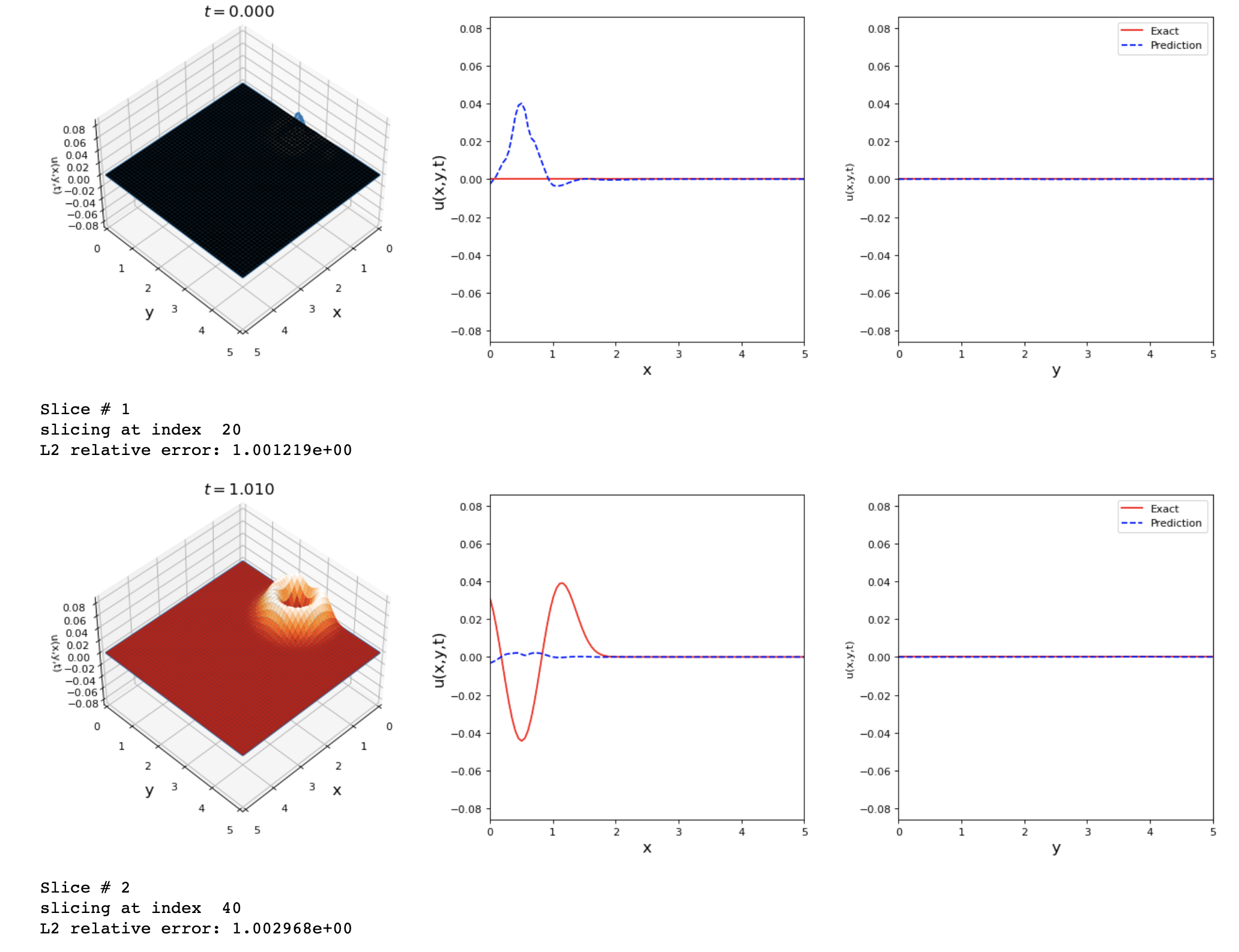
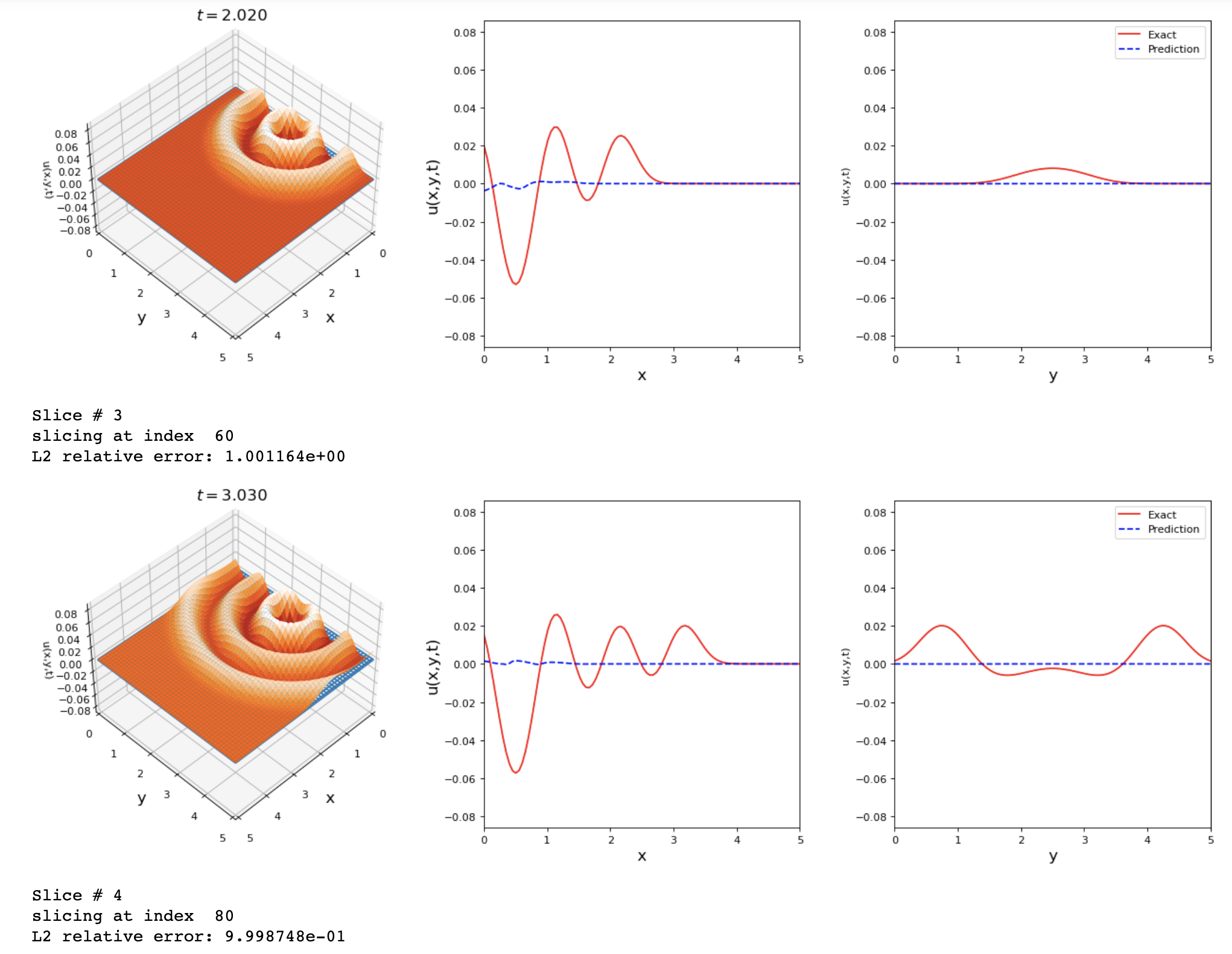
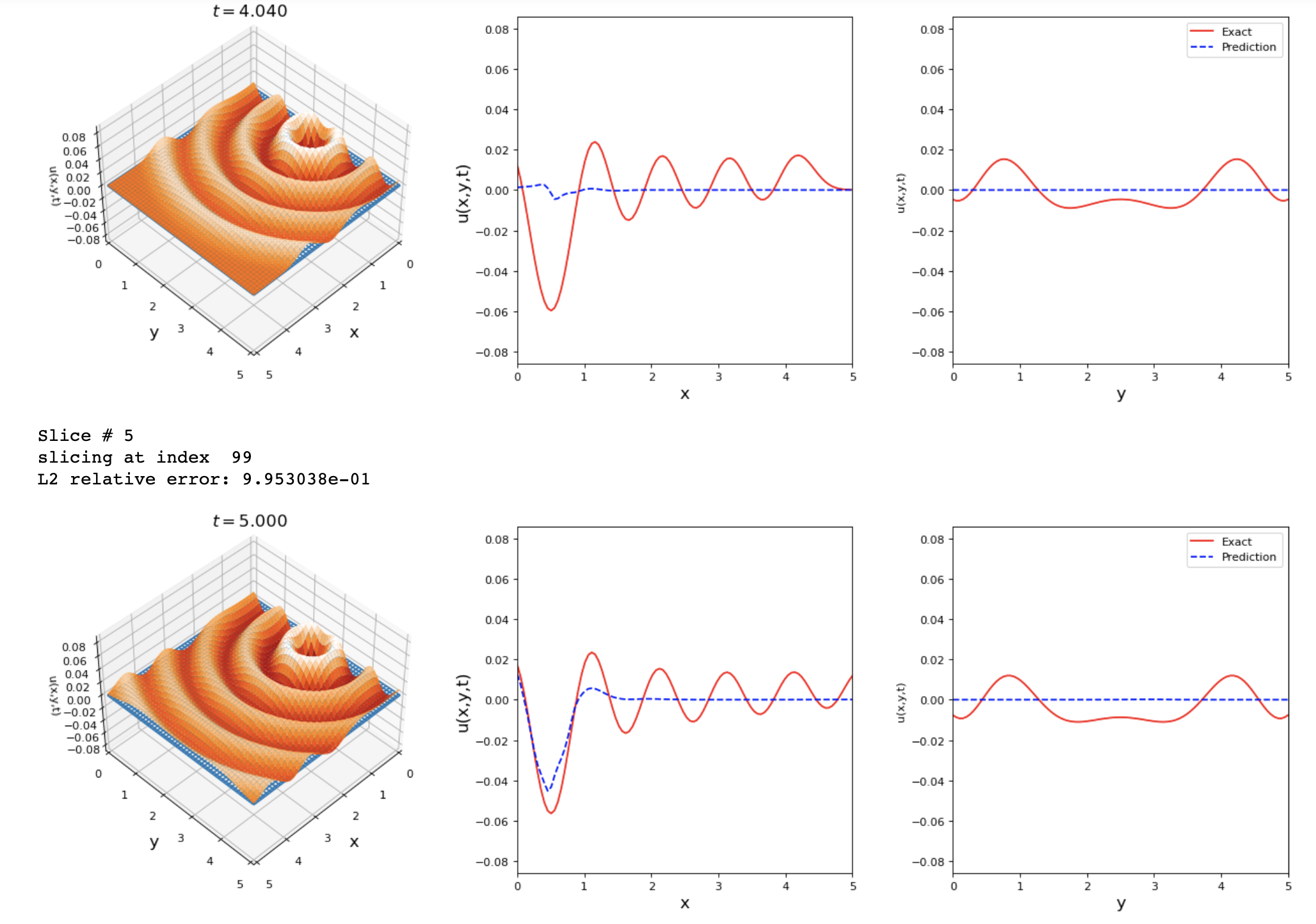
Thank you for the great contribution!
I'm trying to extend the 1D example problems to 2D, but I want to make sure my changes are in the correct place:
Domain = DomainND(["x", "y", "t"], time_var='t')
Domain.add("x", [0.0, 5.0], 100)
Domain.add("y", [0.0, 5.0], 100)
Domain.add("t", [0.0, 5.0], 100)
All of my BCs and ICs are zero. And my equation has a (forcing) time-dependent source term as such:
Please advise.
Looking forward to your reply!
The text was updated successfully, but these errors were encountered: