README_EN.md

64. Minimum Path Sum

中文文档

Description

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

 

Example 1:

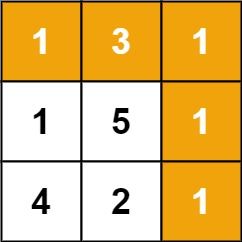
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

Solutions

Python3

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dp = [[grid[0][0]] * n for _ in range(m)]
        for i in range(1, m):
            dp[i][0] = dp[i - 1][0] + grid[i][0]
        for j in range(1, n):
            dp[0][j] = dp[0][j - 1] + grid[0][j]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
        return dp[m - 1][n - 1]

Java

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

C++

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, grid[0][0]));
        for (int i = 1; i < m; ++i) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
};

...