README_EN.md

356. Line Reflection

中文文档

Description

Given n points on a 2D plane, find if there is such a line parallel to y-axis that reflect the given points symmetrically, in other words, answer whether or not if there exists a line that after reflecting all points over the given line the set of the original points is the same that the reflected ones.

Note that there can be repeated points.

Follow up:
Could you do better than O(n²) ?

 

Example 1:

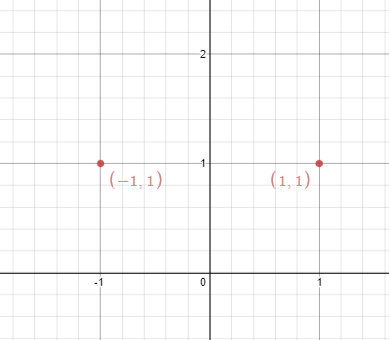
Input: points = [[1,1],[-1,1]]
Output: true
Explanation: We can choose the line x = 0.

Example 2:

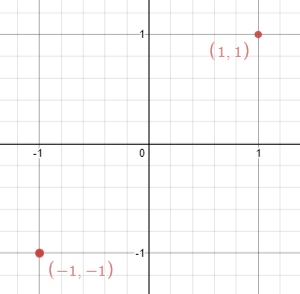
Input: points = [[1,1],[-1,-1]]
Output: false
Explanation: We can't choose a line.

 

Constraints:

• n == points.length
• 1 <= n <= 10^4
• -10^8 <= points[i][j] <= 10^8

Solutions

Python3

class Solution:
    def isReflected(self, points: List[List[int]]) -> bool:
        min_x, max_x = float('inf'), float('-inf')
        point_set = set()
        for x, y in points:
            min_x = min(min_x, x)
            max_x = max(max_x, x)
            point_set.add((x, y))
        s = min_x + max_x
        for x, y in points:
            if (s - x, y) not in point_set:
                return False
        return True

Java

class Solution {
    public boolean isReflected(int[][] points) {
        int minX = Integer.MAX_VALUE, maxX = Integer.MIN_VALUE;
        Set<String> pointSet = new HashSet<>();
        for (int[] point : points) {
            minX = Math.min(minX, point[0]);
            maxX = Math.max(maxX, point[0]);
            pointSet.add(point[0] + "." + point[1]);
        }
        long s = minX + maxX;
        for (int[] point : points) {
            if (!pointSet.contains((s - point[0]) + "." + point[1])) {
                return false;
            }
        }
        return true;
    }
}

...