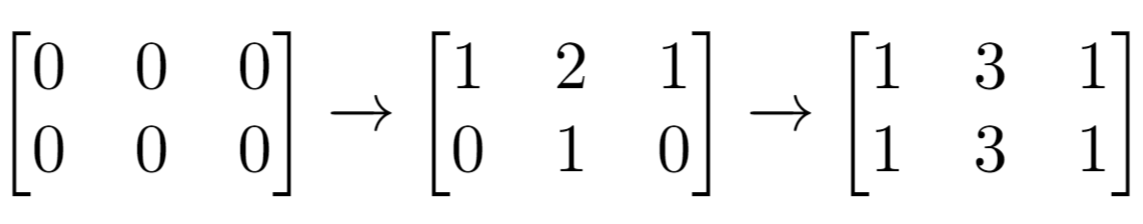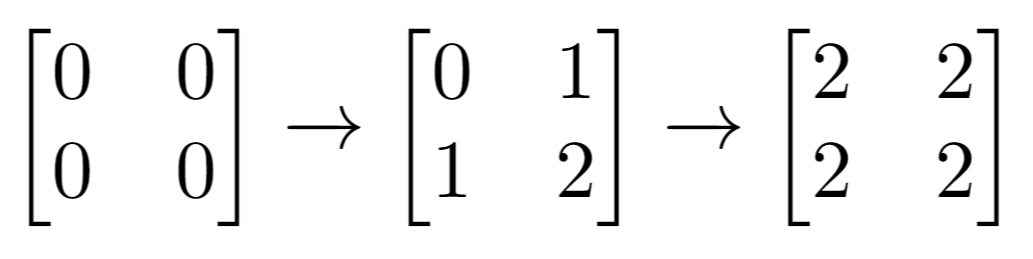给你一个 m x n 的矩阵,最开始的时候,每个单元格中的值都是 0。
另有一个二维索引数组 indices,indices[i] = [ri, ci] 指向矩阵中的某个位置,其中 ri 和 ci 分别表示指定的行和列(从 0 开始编号)。
对 indices[i] 所指向的每个位置,应同时执行下述增量操作:
ri行上的所有单元格,加1。ci列上的所有单元格,加1。
给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后,返回矩阵中 奇数值单元格 的数目。
示例 1:
输入:m = 2, n = 3, indices = [[0,1],[1,1]] 输出:6 解释:最开始的矩阵是 [[0,0,0],[0,0,0]]。 第一次增量操作后得到 [[1,2,1],[0,1,0]]。 最后的矩阵是 [[1,3,1],[1,3,1]],里面有 6 个奇数。
示例 2:
输入:m = 2, n = 2, indices = [[1,1],[0,0]] 输出:0 解释:最后的矩阵是 [[2,2],[2,2]],里面没有奇数。
提示:
1 <= m, n <= 501 <= indices.length <= 1000 <= ri < m0 <= ci < n
进阶:你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗?