README.md

1516. 移动 N 叉树的子树

English Version

题目描述

给定一棵没有重复值的 N 叉树的根节点 root ，以及其中的两个节点 p 和 q。

移动节点 p 及其子树，使节点 p 成为节点 q 的直接子节点。如果 p 已经是 q 的直接子节点，则请勿改动任何节点。节点 p 必须是节点 q 的子节点列表的最后一项。

返回改动后的树的根节点。

 

节点 p 和 q 可能是下列三种情况之一：

1. 节点 q 在节点 p 的子树中。
2. 节点 p 在节点 q 的子树中。
3. 节点 p 不在节点 q 的子树中，且节点 q 也不在节点 p 的子树中。

在第 2 种和第 3 种情况中，你只需要移动 p （及其子树），使 p 成为 q 的子节点。但是在第 1 种情况中，树的节点可能会断连，因此你还需要重新连接这些节点。请在解题前仔细阅读示例。

 

N 叉树的输入序列以层序遍历的形式给出，每组子节点用 null 分隔（见示例）。

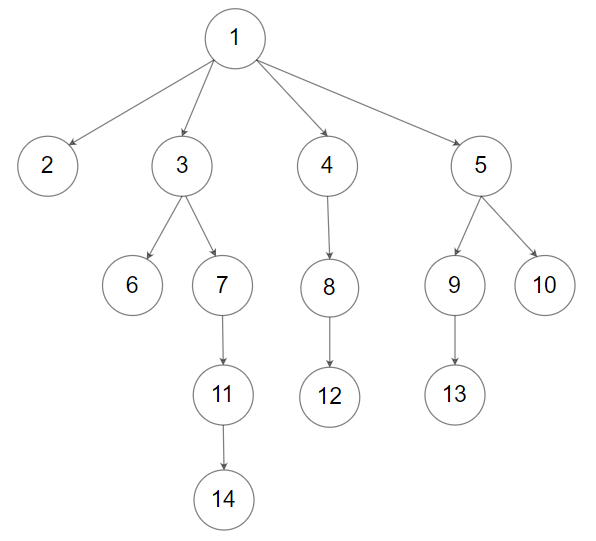
例如，上面的树会被序列化为 [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]。

 

示例 1:

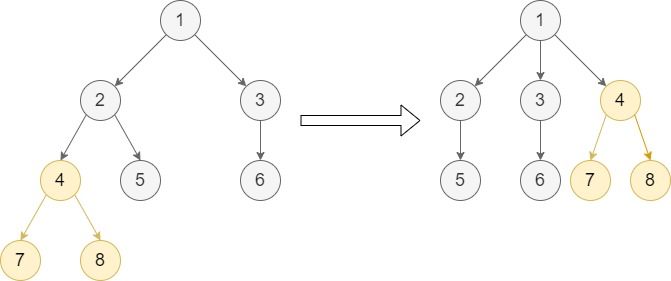
输入: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 4, q = 1
输出: [1,null,2,3,4,null,5,null,6,null,7,8]
解释: 该示例属于第二种情况，节点 p 在节点 q 的子树中。我们可以移动节点 p 及其子树，使 p 成为节点 q 的直接子节点。
注意，节点 4 是节点 1 的最后一个子节点。

示例 2:

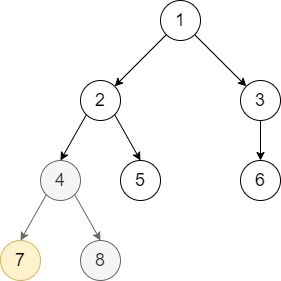
输入: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 7, q = 4
输出: [1,null,2,3,null,4,5,null,6,null,7,8]
解释: 节点 7 已经是节点 4 的直接子节点，因此我们不改动任何节点。

示例 3:

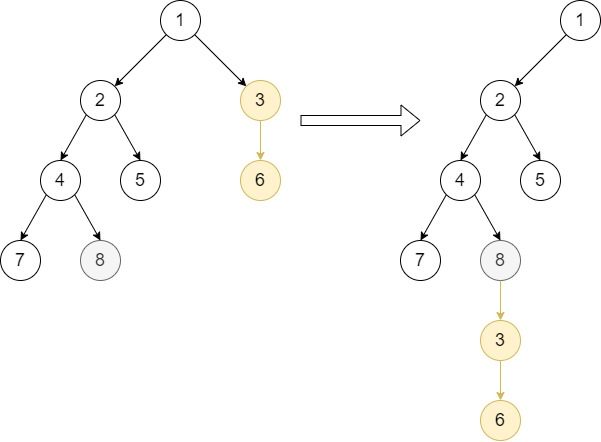
输入: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 3, q = 8
输出: [1,null,2,null,4,5,null,7,8,null,null,null,3,null,6]
解释: 该示例属于第三种情况，节点 p 不在节点 q 的子树中，反之亦然。我们可以移动节点 3 及其子树，使之成为节点 8 的子节点。

示例 4:

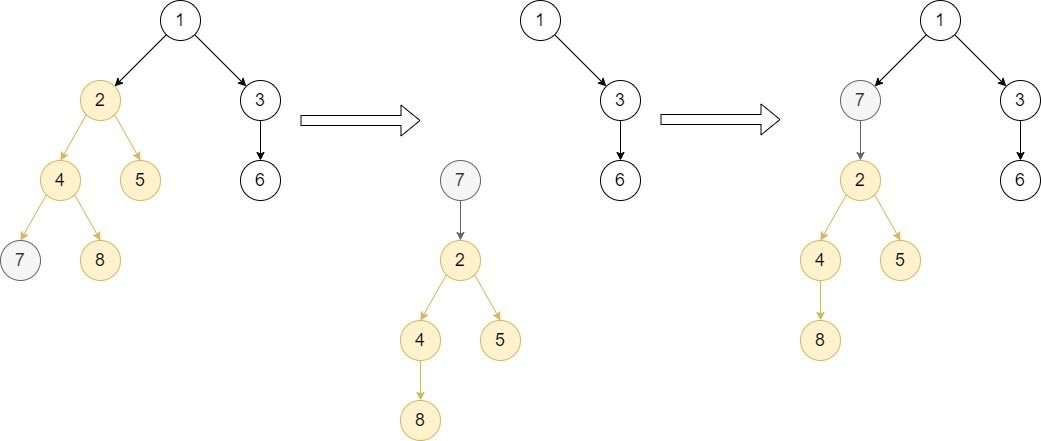
输入: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 2, q = 7
输出: [1,null,7,3,null,2,null,6,null,4,5,null,null,8]
解释: 节点 q 在节点 p 的子树中，因此该示例属于第一种情况。
第一步，我们移动节点 p （及其所有子树，除节点 q 的子树外），并将其加入节点 q 的子节点列表中。
然后我们发现树已断连，你需要重新连接节点 q 来代替节点 p，如图所示。

示例 5:

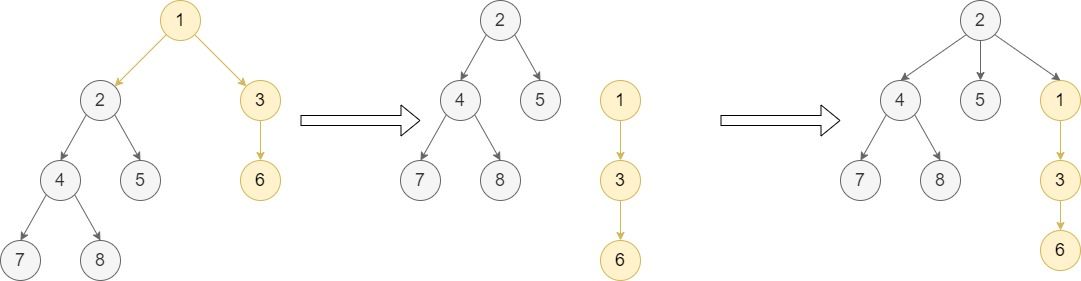
输入: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 1, q = 2
输出: [2,null,4,5,1,null,7,8,null,null,3,null,null,null,6]
解释: 节点 q 在节点 p 的子树中，因此该示例属于第一种情况。
第一步，我们移动节点 p （及其所有子树，除节点 q 的子树外），并将其加入节点 q 的子节点列表中。
因为节点 p 是原树的根节点，因此节点 q 代替之成为新树的根节点。

 

提示:

• 节点的总数在 [2, 1000] 间。
• 每个节点都有唯一的值。
• p != null
• q != null
• p 和 q 是两个不同的节点（即 p != q ）。

解法

Python3

Java

...