You want to compute the Fourier transform of a signal, but your signal can be corrupted by outliers? If so, this package is for you even though you will have to say goodbye to the "fast" in Fast Fourier Transform 🏃🙅♀️
The package can be installed from PyPI with
pip install robust_fourierIf speed matters for you, you can also install the package with the optional dependency
numba
pip install robust_fourier[fast]To install the package from GitHub, you can simply clone the repository
git clone https://github.com/MothNik/robust_fourier.gitFor the following commands, a Makefile is provided to simplify the process. Its use is
optional, but recommended.
From within the repositories root directory, the package can be installed for normal use
# ⚠️ first, activate your virtual environment, e.g., source venv/bin/activate
make install
# equivalent to
pip install --upgrade .or for development (with all the development dependencies)
# ⚠️ first, activate your virtual environment, e.g., source venv/bin/activate
make install-dev
# equivalent to
pip install --upgrade .["dev"]When working in developer mode, an environment variable has to be added to run certain scripts.
ROBFT_DEVELOPER = true
The following checks for black, isort, pyright, mypy, pycodestyle, and
ruff - that are also part of the CI pipeline - can be run with
make black-check
make isort-check
make pyright-check
make mypy-check
make pycodestyle-check
make ruff-check
# or for all at once
make check
# equivalent to
black --check --diff --color ./auxiliary_scripts ./examples ./src ./tests
isort --check --diff --color ./auxiliary_scripts ./examples ./src ./tests
pyright ./auxiliary_scripts ./examples ./src ./tests
mypy ./auxiliary_scripts ./examples ./src ./tests
ruff check ./auxiliary_scripts ./examples ./src ./tests
pycodestyle ./auxiliary_scripts ./examples ./src ./tests --max-line-length=88 --ignore=E203,W503,E704To run the tests - almost like in the CI pipeline - you can use
make test-xmlcov # for an XML report
make test-htmlcov # for an HTML report
# equivalent to
pytest --cov=robust_fourier ./tests -n="auto" --cov-report=xml -x --no-jit
pytest --cov=robust_fourier ./tests -n="auto" --cov-report=html -x --no-jitfor parallelized testing whose coverage report will be stored in the file
./coverage.xml or in the folder ./htmlcov, respectively.
Being the eigenfunctions of the Fourier transform, Hermite functions are excellent candidates for the basis functions for a Least Squares Regression approach to the Fourier transform. However, their evaluation can be a bit tricky.
The module hermite_functions offers a numerically stable way to evaluate Hermite
functions or arbitrary order
After a slight modification of the definitions in [1], the Hermite functions can be written as
with the Hermite polynomials
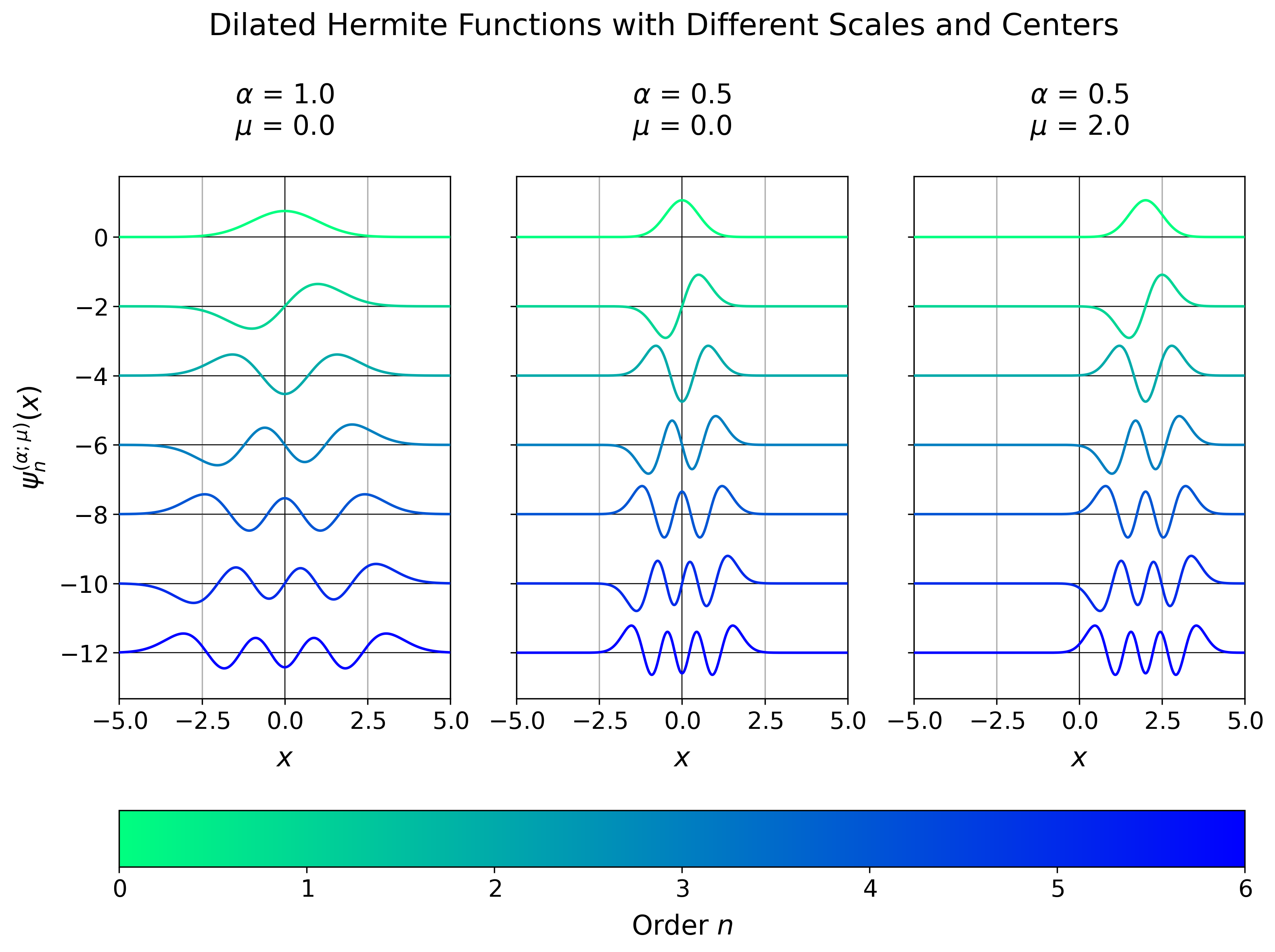
With robust_fourier, the Hermite functions can be evaluated for arbitrary orders
using the function interface hermite_function_vander
import numpy as np
from robust_fourier import hermite_function_vander
ORDER_MAX = 25 # the maximum order of the Hermite functions
ALPHA = 2.0 # the scaling factor for the x-variable
MU = -2.0 # the shift of the x-variable
X_FROM = -20.0
X_TO = 20.0
NUM_X = 10_001
x_values = np.linspace(start=X_FROM + MU, stop=X_TO + MU, num=NUM_X)
hermite_vander = hermite_function_vander(
x=x_values,
n=ORDER_MAX,
alpha=ALPHA,
x_center=MU,
jit=True, # will only take effect if Numba is installed
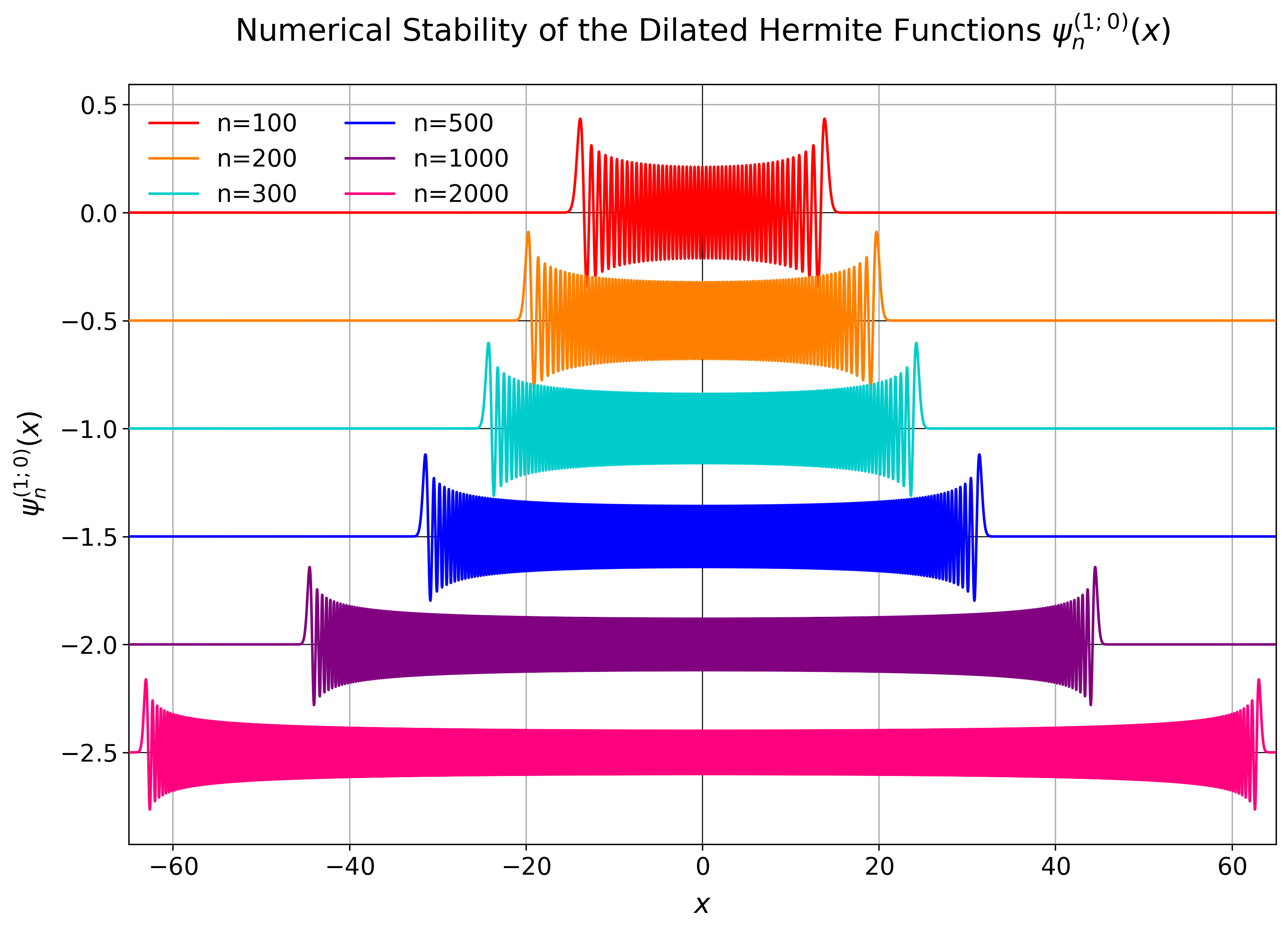
)By making use of logarithm tricks, the evaluation that might involve infinitely high polynomial values and at the same time infinitely small Gaussians - that are on top of that scaled by an infinitely high factorial - can be computed safely and yield accurate results.
For doing so, the relation between the dilated and the non-dilated Hermite functions
and the recurrence relation for the Hermite functions
are used, but not directly. Instead, the latest evaluated Hermite function is kept at a value of either -1, 0, or +1 during the recursion and the logarithm of a correction factor is tracked and applied when the respective Hermite function is finally evaluated and stored. This approach is based on [2].
The implementation is tested against a symbolic evaluation with sympy that uses 200
digits of precision and it can be shown that even orders as high as 2,000 can still be
computed even though neither the polynomial, the Gaussian nor the factorial can be
evaluated for this anymore. The factorial for example would already have overflown for
orders of 170 in float64-precision.
As a sanity check, their orthogonality is part of the tests together with a test for
the fact that the absolute values of the Hermite functions for real input cannot exceed
the value
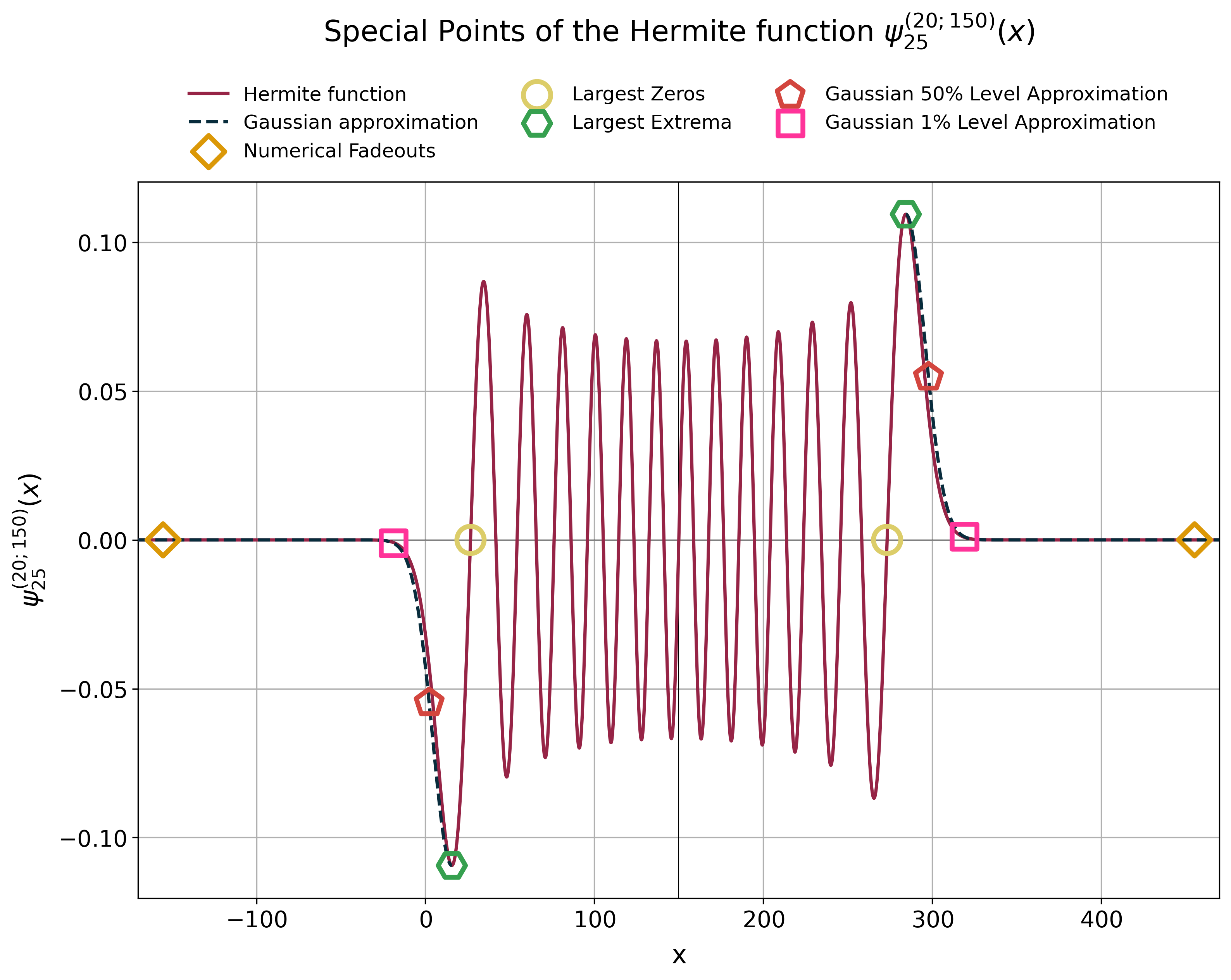
On top of that robust_fourier comes with utility functions to approximate some
special points of the Hermite functions, namely the x-positions of their
- largest root (= outermost zero),
- largest extrema in the outermost oscillation,
- the point where they numerically fade to zero, and
- an approximation of the outermost oscillation (tail) by a conservative Gaussian peak.
import numpy as np
from robust_fourier import hermite_approx
ORDER = 25 # the order of the Hermite functions
ALPHA = 20.0 # the scaling factor for the x-variable
MU = 150.0 # the shift of the x-variable
X_FROM = -65.0
X_TO = 65.0
NUM_X = 100_001
# 1) the x-positions at which the outermost oscillation fades below machine
# precision
x_fadeout = hermite_approx.x_fadeout(
n=ORDER,
alpha=ALPHA,
x_center=MU,
)
# 2) the x-positions of the largest zeros
x_largest_zero = hermite_approx.x_largest_zeros(
n=ORDER,
alpha=ALPHA,
x_center=MU,
)
# 3) the x-positions of the largest extrema
x_largest_extremum = hermite_approx.x_largest_extrema(
n=ORDER,
alpha=ALPHA,
x_center=MU,
)
# 4) the Gaussian approximation of the outermost oscillation ...
left_gaussian, right_gaussian = hermite_approx.get_tail_gauss_fit(
n=ORDER,
alpha=ALPHA,
x_center=MU,
)
# ... which is solved for the 50% level
x_left_fifty_percent = left_gaussian.solve_for_y_fraction(y_fraction=0.5)
x_right_fifty_percent = right_gaussian.solve_for_y_fraction(y_fraction=0.5)
# ... but can also be evaluated for all x-values
x_values = np.linspace(start=X_FROM + MU, stop=X_TO + MU, num=NUM_X)
left_gaussian_values = left_gaussian(x=x_values)
right_gaussian_values = right_gaussian(x=x_values)
# 5) the Gaussian approximation is also solved for the 1% interval as a more
# realistic (less conservative) approximation of the fadeout point
x_one_percent = hermite_approx.x_tail_drop_to_fraction(
n=ORDER,
y_fraction=0.01,
alpha=ALPHA,
x_center=MU,
).ravel()Even though the Hermite functions have some nice properties,
they are not necessarily the best choice for the Fourier transform. Choosing their
scaling parameter
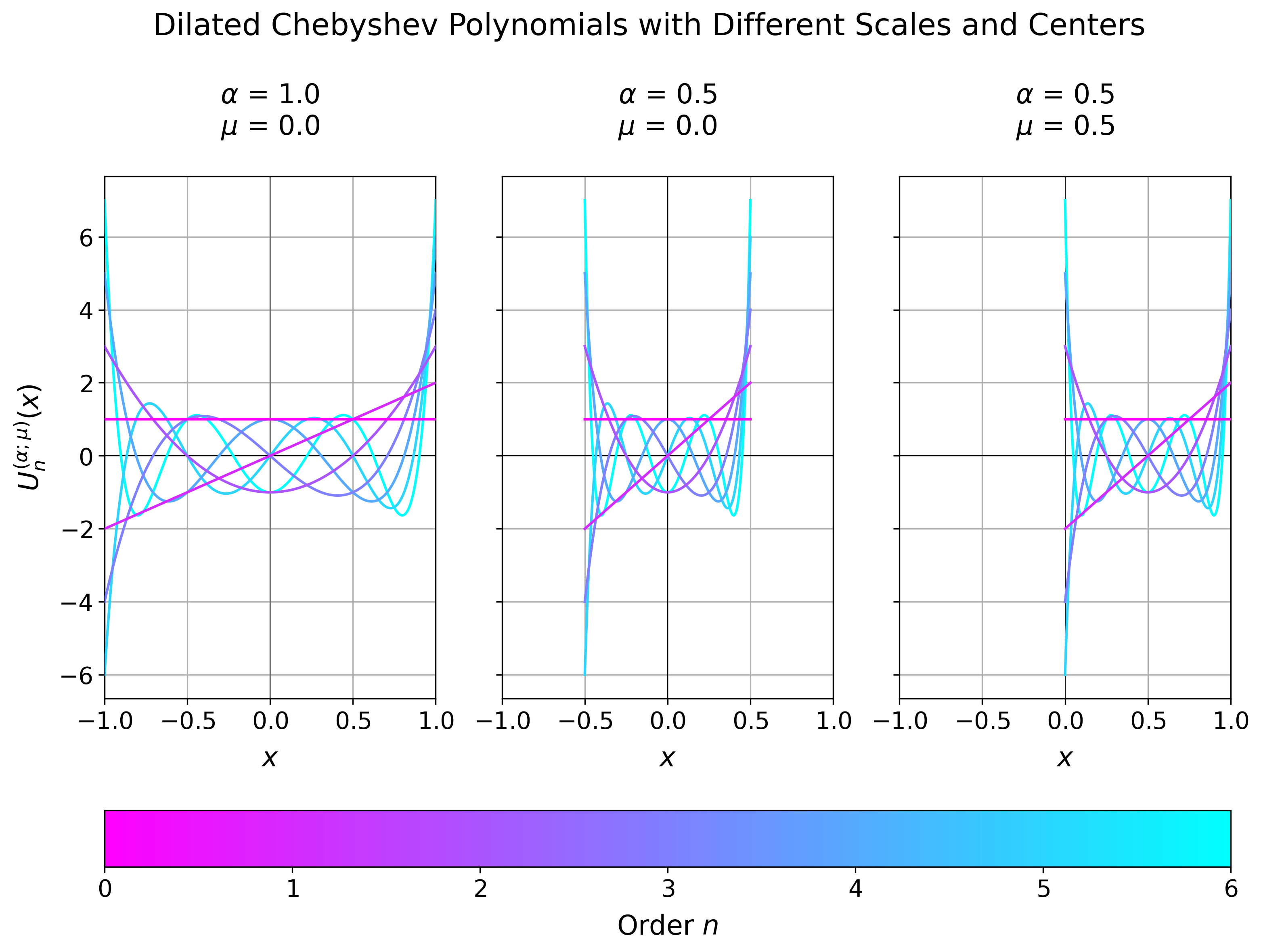
for the first kind and
for the second kind. In [3] the second kind robust_fourier
import numpy as np
from robust_fourier import chebyshev_polyvander
ORDER_MAX = 10 # the maximum order of the Chebyshev polynomials
ALPHA = 0.5 # the scaling factor for the x-variable
MU = 0.5 # the shift of the x-variable
X_FROM = -0.5
X_TO = 0.5
NUM_X = 10_001
x_values = np.linspace(start=X_FROM + MU, stop=X_TO + MU, num=NUM_X)
chebyshev_vander_first_kind = chebyshev_polyvander(
x=x_values,
n=ORDER_MAX,
alpha=ALPHA,
x_center=MU,
kind="first",
jit=True, # will only take effect if Numba is installed
)
chebyshev_vander_second_kind = chebyshev_polyvander(
x=x_values,
n=ORDER_MAX,
alpha=ALPHA,
x_center=MU,
kind="second",
jit=True, # will only take effect if Numba is installed
)
# alternatively, both kinds can be computed in one go because this is how they are
# computed internally to achieve maximum accuracy
(
chebyshev_vander_first_kind,
chebyshev_vander_second_kind,
) = chebyshev_polyvander(
x=x_values,
n=ORDER_MAX,
alpha=ALPHA,
x_center=MU,
kind="both",
jit=True, # will only take effect if Numba is installed
)🏗️🚧 👷👷♂️👷♀️🏗️🚧
Currently under construction. Please check back later.
This package would not have been possible without the - unfortunately apparently
abandoned - package hermite-functions
which was a great inspiration for the implementation of the Hermite functions.
On top of that, I hereby want to thank the anonymous support that patiently listened to my endless talks about the greatness of Hermite functions (even though they cannot keep up with her) and that also helped me to give the plots the visual appeal they have now 🤩.
- [1] Dobróka M., Szegedi H., and Vass P., Inversion-Based Fourier Transform as a New Tool for Noise Rejection, Fourier Transforms - High-tech Application and Current Trends (2017), DOI: http://dx.doi.org/10.5772/66338
- [2] Bunck B. F., A fast algorithm for evaluation of normalized Hermite functions, BIT Numer Math (2009), 49, pp. 281–295, DOI: https://doi.org/10.1007/s10543-009-0216-1
- [3] Al Marashly, O., Dobróka, M., Chebyshev polynomial-based Fourier transformation and its use in low pass filter of gravity data, Acta Geod Geophys (2024), 59, pp. 159–181 DOI: https://doi.org/10.1007/s40328-024-00444-z
- [4] Hrycak T., Schmutzhard S., Accurate evaluation of Chebyshev polynomials in floating-point arithmetic, BIT Numer Math (2019), 59, pp. 403–416, DOI: https://doi.org/10.1007/s10543-018-0738-5