Releases · PennyLaneAI/pennylane

14 Jan 20:40

PietropaoloFrisoni

v0.40.0

19ac94b

Release 0.40.0 Latest

Latest

New features since last release

Efficient state preparation methods 🦾

State preparation tailored for matrix product states (MPS) is now supported with :class:qml.MPSPrep <pennylane.MPSPrep> on the lightning.tensor device. (#6431)

Given a list of $n$ tensors that represents an MPS, $[A^{(0)}, ..., A^{(n-1)}]$, :class:qml.MPSPrep <pennylane.MPSPrep> lets you directly inject the MPS into a QNode as the initial state of the circuit without any need for pre-processing. The first and last tensors in the list must be rank-2, while all intermediate tensors should be rank-3.

import pennylane as qml
import numpy as np

mps = [
    np.array([[0.0, 0.107], [0.994, 0.0]]),
    np.array(
        [
            [[0.0, 0.0, 0.0, -0.0], [1.0, 0.0, 0.0, -0.0]],
            [[0.0, 1.0, 0.0, -0.0], [0.0, 0.0, 0.0, -0.0]],
        ]
    ),
    np.array(
        [
            [[-1.0, 0.0], [0.0, 0.0]],
            [[0.0, 0.0], [0.0, 1.0]],
            [[0.0, -1.0], [0.0, 0.0]],
            [[0.0, 0.0], [1.0, 0.0]],
        ]
    ),
    np.array([[-1.0, -0.0], [-0.0, -1.0]]),
]

dev = qml.device("lightning.tensor", wires = [0, 1, 2, 3])
@qml.qnode(dev)
def circuit():
    qml.MPSPrep(mps, wires = [0,1,2])
    return qml.state()

>>> print(circuit())
[ 0.    +0.j  0.    +0.j  0.    +0.j -0.1066+0.j  0.    +0.j  0.    +0.j
  0.    +0.j  0.    +0.j  0.    +0.j  0.    +0.j  0.    +0.j  0.    +0.j
  0.9943+0.j  0.    +0.j  0.    +0.j  0.    +0.j]

At this time, :class:qml.MPSPrep <pennylane.MPSPrep> is only supported on the lightning.tensor device.

Custom-made state preparation for linear combinations of quantum states is now available with :class:qml.Superposition <pennylane.Superposition>. (#6670)

Given a list of $m$ coefficients $c_i$ and basic states $|b_i\rangle$, :class:qml.Superposition <pennylane.Superposition> prepares $|\phi\rangle = \sum_i^m c_i |b_i\rangle$. Here is a simple example showing how to use :class:qml.Superposition <pennylane.Superposition> to prepare $\tfrac{1}{\sqrt{2}} |00\rangle + \tfrac{1}{\sqrt{2}} |10\rangle$.
```
coeffs = np.array([0.70710678, 0.70710678])
basis =  np.array([[0, 0], [1, 0]])

@qml.qnode(qml.device('default.qubit'))
def circuit():
    qml.Superposition(coeffs, basis, wires=[0, 1], work_wire=[2])
    return qml.state()
```
```
>>> circuit()
Array([0.7071068 +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.70710677+0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j],      dtype=complex64)
```
Note that specification of one work_wire is required.

Enhanced QSVT functionality 🤩

New functionality to calculate and convert phase angles for QSP and QSVT has been added with :func:qml.poly_to_angles <pennylane.poly_to_angles> and :func:qml.transform_angles <pennylane.transform_angles>. (#6483)

The :func:qml.poly_to_angles <pennylane.poly_to_angles> function calculates phase angles directly given polynomial coefficients and the routine in which the angles will be used ("QSVT", "QSP", or "GQSP"):
```
>>> poly = [0, 1.0, 0, -1/2, 0, 1/3]
>>> qsvt_angles = qml.poly_to_angles(poly, "QSVT")
>>> print(qsvt_angles)
[-5.49778714  1.57079633  1.57079633  0.5833829   1.61095884  0.74753829]
```
The :func:qml.transform_angles <pennylane.transform_angles> function can be used to convert angles from one routine to another:
```
>>> qsp_angles = np.array([0.2, 0.3, 0.5])
>>> qsvt_angles = qml.transform_angles(qsp_angles, "QSP", "QSVT")
>>> print(qsvt_angles)
[-6.86858347  1.87079633 -0.28539816]
```

The :func:qml.qsvt <pennylane.qsvt> function has been improved to be more user-friendly, with enhanced capabilities. (#6520) (#6693)

Block encoding and phase angle computation are now handled automatically, given a matrix to encode, polynomial coefficients, and a block encoding method ("prepselprep", "qubitization", "embedding", or "fable", all implemented with their corresponding operators in PennyLane).

# P(x) = -x + 0.5 x^3 + 0.5 x^5
poly = np.array([0, -1, 0, 0.5, 0, 0.5])
hamiltonian = qml.dot([0.3, 0.7], [qml.Z(1), qml.X(1) @ qml.Z(2)])

dev = qml.device("default.qubit")
@qml.qnode(dev)
def circuit():
    qml.qsvt(hamiltonian, poly, encoding_wires=[0], block_encoding="prepselprep")
    return qml.state()

matrix = qml.matrix(circuit, wire_order=[0, 1, 2])()

>>> print(matrix[:4, :4].real)
[[-0.1625  0.     -0.3793  0.    ]
 [ 0.     -0.1625  0.      0.3793]
 [-0.3793  0.      0.1625  0.    ]
 [ 0.      0.3793  0.      0.1625]]

The old functionality can still be accessed with :func:qml.qsvt_legacy <pennylane.qsvt_legacy>.

A new :class:qml.GQSP <pennylane.GQSP> template has been added to perform Generalized Quantum Signal Processing (GQSP). (#6565) Similar to QSVT, GQSP is an algorithm that polynomially transforms an input unitary operator, but with fewer restrictions on the chosen polynomial.

You can also use :func:qml.poly_to_angles <pennylane.poly_to_angles> to obtain angles for GQSP!

# P(x) = 0.1 + 0.2j x + 0.3 x^2
poly = [0.1, 0.2j, 0.3]
angles = qml.poly_to_angles(poly, "GQSP")

@qml.prod # transforms the qfunc into an Operator
def unitary(wires):
    qml.RX(0.3, wires)

dev = qml.device("default.qubit")
@qml.qnode(dev)
def circuit(angles):
    qml.GQSP(unitary(wires = 1), angles, control = 0)
    return qml.state()

matrix = qml.matrix(circuit, wire_order=[0, 1])(angles)
``` ```pycon
>>> print(np.round(matrix,3)[:2, :2])
[[0.387+0.198j 0.03 -0.089j]
[0.03 -0.089j 0.387+0.198j]]

Generalized Trotter products 🐖

Trotter products that work on exponentiated operators directly instead of full system hamiltonians can now be encoded into circuits with the addition of :class:qml.TrotterizedQfunc <pennylane.TrotterizedQfunc> and :func:qml.trotterize <pennylane.trotterize>. This allows for custom specification of the first-order expansion of the Suzuki-Trotter product formula and extrapolating it to the $n^{\text{th}}$ order. (#6627)

If the first-order of the Suzuki-Trotter product formula for a given problem is known, :class:qml.TrotterizedQfunc <pennylane.TrotterizedQfunc> and :func:qml.trotterize <pennylane.trotterize> let you implement the $n^{\text{th}}$-order product formula while only specifying the first-order term as a quantum function.
```
def my_custom_first_order_expansion(time, theta, phi, wires, flip):
  qml.RX(time * theta, wires[0])
  qml.RY(time * phi, wires[1])
  if flip:
      qml.CNOT(wires=wires[:2])
```
:func:qml.trotterize <pennylane.trotterize> requires the quantum function representing the first-order product formula, the number of Trotter steps, and the desired order. It returns a function with the same call signature as the first-order product formula quantum function:
```
@qml.qnode(qml.device("default.qubit"))
def my_circuit(time, theta, phi, num_trotter_steps):
    qml.trotterize(
        first_order_expansion,
        n=num_trotter_steps,
        order=2,
    )(time, theta, phi, wires=['a', 'b'], flip=True)
    return qml.state()
```
Alternatively, :class:qml.TrotterizedQfunc <pennylane.TrotterizedQfunc> can be used as follows:
```
@qml.qnode(qml.device("default.qubit"))
def my_circuit(time, theta, phi, num_trotter_steps):
    qml.TrotterizedQfunc(
        time,
        theta,
        phi,
        qfunc=my_custom_first_order_expansion,
        n=num_trotter_steps,
        order=2,
        wires=['a', 'b'],
        flip=True,
    )
    return qml.state()
```
```
>>> time = 0.1
>>> theta, phi = (0.12, -3.45)
>>> print(qml.draw(my_circuit, level="device")(time, theta, phi, num_trotter_steps=1))
a: ──RX(0.01)──╭●─╭●──RX(0.01)──┤  State
b: ──RY(-0.17)─╰X─╰X──RY(-0.17)─┤  State
```
Both methods produce the same results, but offer different interfaces based on the application or overall preference.

Bosonic operators 🎈

A new module, :mod:qml.bose <pennylane.bose>, has been added to PennyLane that includes support for constructing and manipulating Bosonic operators and converting between Bosonic operators and qubit operators.

Bosonic operators analogous to qml.FermiWord and qml.FermiSentence are now available with :class:qml.BoseWord <pennylane.BoseWord> and :class:qml.BoseSentence <pennylane.BoseSentence>. (#6518)

:class:qml.BoseWord <pennylane.BoseWord> and :class:qml.BoseSentence <pennylane.BoseSentence> operate similarly to their fermionic counterparts. To create a Bose word, a dictionary is required as input, where the keys are tuples of boson indices and values are '+/-' (denoting the bosonic creation/annihilation operators). For example, the $b^{\dagger}_0 b_1$ can be constructed as follows.
```
>>> w = qml.BoseWord({(0, 0) : '+', (1, 1) : '-'})
>>> print(w)
b⁺(0) b(1)
```
Multiple Bose words can then be combined to form a Bose sentence:
```
>>> w1 = qml.BoseWord({(0, 0) : '+', (1, 1) : '-'})
>>> w2 = qml.BoseWo...
```

Assets 2

05 Nov 19:09

mudit2812

v0.39.0

51797f7

Release 0.39.0

New features since last release

Creating spin Hamiltonians on lattices 💞

Functionality for creating custom Hamiltonians on arbitrary lattices has been added. (#6226) (#6237)

Hamiltonians beyond the available boiler-plate ones in the qml.spin module can be created with the addition of three new functions:
- qml.spin.Lattice: a new object for instantiating customized lattices via primitive translation vectors and unit cell parameters,
- qml.spin.generate_lattice: a utility function for creating standard Lattice objects, including 'chain', 'square', 'rectangle', 'triangle', 'honeycomb', 'kagome', 'lieb', 'cubic', 'bcc', 'fcc', and 'diamond',
- qml.spin.spin_hamiltonian: generates a spin Hamiltonian object given a Lattice object with custom edges/nodes.
An example is shown below for a $3 \times 3$ triangular lattice with open boundary conditions.
```
lattice = qml.spin.Lattice(
    n_cells=[3, 3],
    vectors=[[1, 0], [np.cos(np.pi/3), np.sin(np.pi/3)]],
    positions=[[0, 0]],
    boundary_condition=False
)
```
We can validate this lattice against qml.spin.generate_lattice('triangle', ...) by checking the lattice_points (the $(x, y)$ coordinates of all sites in the lattice):
```
>>> lp = lattice.lattice_points
>>> triangular_lattice = qml.spin.generate_lattice('triangle', n_cells=[3, 3])
>>> np.allclose(lp, triangular_lattice.lattice_points)
True
```
The edges of the Lattice object are nearest-neighbour by default, where we can add edges by using its add_edge method.

Optionally, a Lattice object can have interactions and fields endowed to it by specifying values for its custom_edges and custom_nodes keyword arguments. The Hamiltonian can then be extracted with the qml.spin.spin_hamiltonian function. An example is shown below for the transverse-field Ising model Hamiltonian on a $3 \times 3$ triangular lattice. Note that the custom_edges and custom_nodes keyword arguments only need to be defined for one unit cell repetition.
```
edges = [
    (0, 1), (0, 3), (1, 3)
]

lattice = qml.spin.Lattice(
    n_cells=[3, 3],
    vectors=[[1, 0], [np.cos(np.pi/3), np.sin(np.pi/3)]],
    positions=[[0, 0]],
    boundary_condition=False,
    custom_edges=[[edge, ("ZZ", -1.0)] for edge in edges], 
    custom_nodes=[[i, ("X", -0.5)] for i in range(3*3)],
)
```
```
>>> tfim_ham = qml.spin.transverse_ising('triangle', [3, 3], coupling=1.0, h=0.5)
>>> tfim_ham == qml.spin.spin_hamiltonian(lattice=lattice)
True
```
More industry-standard spin Hamiltonians have been added in the qml.spin module. (#6174) (#6201)

Three new industry-standard spin Hamiltonians are now available with PennyLane v0.39:
- qml.spin.emery : the Emery model
- qml.spin.haldane : the Haldane model
- qml.spin.kitaev : the Kitaev model
These additions accompany qml.spin.heisenberg, qml.spin.transverse_ising, and qml.spin.fermi_hubbard, which were introduced in v0.38.

Calculating Polynomials 🔢

Polynomial functions can now be easily encoded into quantum circuits with qml.OutPoly. (#6320)

A new template called qml.OutPoly is available, which provides the ability to encode a polynomial function in a quantum circuit. Given a polynomial function $f(x_1, x_2, \cdots, x_N)$, qml.OutPoly requires:
- f : a standard Python function that represents $f(x_1, x_2, \cdots, x_N)$,
- input_registers ($\vert x_1 \rangle$, $\vert x_2 \rangle$, ..., $\vert x_N \rangle$) : a list/tuple containing Wires objects that correspond to the embedded numeric values of $x_1, x_2, \cdots, x_N$,
- output_wires : the Wires for which the numeric value of $f(x_1, x_2, \cdots, x_N)$ is stored.
Here is an example of using qml.OutPoly to calculate $f(x_1, x_2) = 3x_1^2 - x_1x_2$ for $f(1, 2) = 1$.
```
wires = qml.registers({"x1": 1, "x2": 2, "output": 2})

def f(x1, x2):
    return 3 * x1 ** 2 - x1 * x2

@qml.qnode(qml.device("default.qubit", shots = 1))
def circuit():
    # load values of x1 and x2
    qml.BasisEmbedding(1, wires=wires["x1"])
    qml.BasisEmbedding(2, wires=wires["x2"])

    # apply the polynomial
    qml.OutPoly(
        f,
        input_registers = [wires["x1"], wires["x2"]],
        output_wires = wires["output"])

    return qml.sample(wires=wires["output"])
```
```
>>> circuit()
array([0, 1])
```
The result, [0, 1], is the binary representation of $1$. By default, the result is calculated modulo $2^\text{len(output wires)}$ but can be overridden with the mod keyword argument.

Readout Noise 📠

Readout errors can now be included in qml.NoiseModel and qml.add_noise with the new qml.noise.meas_eq function. (#6321)

Measurement/readout errors can be specified in a similar fashion to regular gate noise in PennyLane: a newly added Boolean function called qml.noise.meas_eq that accepts a measurement function (e.g., qml.expval, qml.sample, or any other function that can be returned from a QNode) that, when present in the QNode, inserts a noisy operation via qml.noise.partial_wires or a custom noise function. Readout noise in PennyLane also follows the insertion convention, where the specified noise is inserted before the measurement.

Here is an example of adding qml.PhaseFlip noise to any qml.expval measurement:

c0 = qml.noise.meas_eq(qml.expval)
n0 = qml.noise.partial_wires(qml.PhaseFlip, 0.2)

To include this in a qml.NoiseModel, use its meas_map keyword argument:

# gate-based noise
c1 = qml.noise.wires_in([0, 2]) 
n1 = qml.noise.partial_wires(qml.RY, -0.42)

noise_model = qml.NoiseModel({c1: n1}, meas_map={c0: n0})

>>> noise_model
NoiseModel({
  WiresIn([0, 2]): RY(phi=-0.42)
},
meas_map = {
    MeasEq(expval): PhaseFlip(p=0.2)
})

qml.noise.meas_eq can also be combined with other Boolean functions in qml.noise via bitwise operators for more versatility.

To add this noise_model to a circuit, use the qml.add_noise transform as per usual. For example,

@qml.qnode(qml.device("default.mixed", wires=3))
def circuit():
    qml.RX(0.1967, wires=0)
    for i in range(3):
        qml.Hadamard(i)

    return qml.expval(qml.X(0) @ qml.X(1))

>>> noisy_circuit = qml.add_noise(circuit, noise_model)
>>> print(qml.draw(noisy_circuit)())
0: ──RX(0.20)──RY(-0.42)────────H──RY(-0.42)──PhaseFlip(0.20)─┤ ╭<X@X>
1: ──H─────────PhaseFlip(0.20)────────────────────────────────┤ ╰<X@X>
2: ──H─────────RY(-0.42)──────────────────────────────────────┤    
>>> print(circuit(), noisy_circuit())
0.9807168489852615 0.35305806563469433

User-friendly decompositions 📠

A new transform called qml.transforms.decompose has been added to better facilitate the custom decomposition of operators in PennyLane circuits. (#6334)

Previous to the addition of qml.transforms.decompose, decomposing operators in PennyLane had to be done by specifying a stopping_condition in qml.device.preprocess.decompose. With qml.transforms.decompose, the user-interface for specifying decompositions is much simpler and more versatile.

Decomposing gates in a circuit can be done a few ways:

Specifying a gate_set comprising PennyLane Operators to decompose into:

from functools import partial

dev = qml.device('default.qubit')
allowed_gates = {qml.Toffoli, qml.RX, qml.RZ}

@partial(qml.transforms.decompose, gate_set=allowed_gates)
@qml.qnode(dev)
def circuit():
    qml.Hadamard(wires=[0])
    qml.Toffoli(wires=[0, 1, 2])
    return qml.expval(qml.Z(0))

>>> print(qml.draw(circuit)())
0: ──RZ(1.57)──RX(1.57)──RZ(1.57)─╭●─┤  <Z>
1: ───────────────────────────────├●─┤
2: ───────────────────────────────╰X─┤

Specifying a gate_set that is defined by a rule (Boolean function). For example, one can specify an arbitrary gate set to decompose into, so long as the resulting gates only act on one or two qubits:

@partial(qml.transforms.decompose, gate_set = lambda op: len(op.wires) <= 2)
@qml.qnode(dev)
def circuit():
    qml.Toffoli(wires=[0, 1, 2])
    return qml.expval(qml.Z(0))

>>> print(qml.draw(circuit)())
0: ───────────╭●───────────╭●────╭●──T──╭●─┤  <Z>
1: ────╭●─────│─────╭●─────│───T─╰X──T†─╰X─┤     
2: ──H─╰X──T†─╰X──T─╰X──T†─╰X──T──H────────┤

Specifying a value for max_expansion. By default, decomposition occurs recursively until the desired gate set is reached, but this can be overridden to control the number of passes.

phase = 1.0
target_wires = [0]
unitary = qml.RX(phase, wires=0).matrix()
n_estimation_wires = 1
estimation_wires = range(1, n_estimation_wires + 1)

def qfunc():
    qml.QuantumPhaseEstimation(
        unitary,
        target_wires=target_wires,
        est...

Assets 2

03 Sep 22:39

mudit2812

v0.38.0

9ba6205

Release 0.38.0

New features since last release

Registers of wires 🧸

A new function called qml.registers has been added that lets you seamlessly create registers of wires. (#5957) (#6102)

Using registers, it is easier to build large algorithms and circuits by applying gates and operations to predefined collections of wires. With qml.registers, you can create registers of wires by providing a dictionary whose keys are register names and whose values are the number of wires in each register.

>>> wire_reg = qml.registers({"alice": 4, "bob": 3})
>>> wire_reg
{'alice': Wires([0, 1, 2, 3]), 'bob': Wires([4, 5, 6])}

The resulting data structure of qml.registers is a dictionary with the same register names as keys, but the values are qml.wires.Wires instances.

Nesting registers within other registers can be done by providing a nested dictionary, where the ordering of wire labels is based on the order of appearance and nestedness.

>>> wire_reg = qml.registers({"alice": {"alice1": 1, "alice2": 2}, "bob": {"bob1": 2, "bob2": 1}})
>>> wire_reg
{'alice1': Wires([0]), 'alice2': Wires([1, 2]), 'alice': Wires([0, 1, 2]), 'bob1': Wires([3, 4]), 'bob2': Wires([5]), 'bob': Wires([3, 4, 5])}

Since the values of the dictionary are Wires instances, their use within quantum circuits is very similar to that of a list of integers.

dev = qml.device("default.qubit")

@qml.qnode(dev)
def circuit():
    for w in wire_reg["alice"]:
        qml.Hadamard(w)

    for w in wire_reg["bob1"]:
        qml.RX(0.1967, wires=w)

    qml.CNOT(wires=[wire_reg["alice1"][0], wire_reg["bob2"][0]])

    return [qml.expval(qml.Y(w)) for w in wire_reg["bob1"]]

print(qml.draw(circuit)())

0: ──H────────╭●─┤     
1: ──H────────│──┤     
2: ──H────────│──┤     
3: ──RX(0.20)─│──┤  <Y>
4: ──RX(0.20)─│──┤  <Y>
5: ───────────╰X─┤

In tandem with qml.registers, we've also made the following improvements to qml.wires.Wires:

Wires instances now have a more copy-paste friendly representation when printed. (#5958)

>>> from pennylane.wires import Wires
>>> w = Wires([1, 2, 3])
>>> w
Wires([1, 2, 3])

Python set-based combinations are now supported by Wires. (#5983)

This new feature unlocks the ability to combine Wires instances in the following ways:

intersection with & or intersection():

>>> wires1 = Wires([1, 2, 3])
>>> wires2 = Wires([2, 3, 4])
>>> wires1.intersection(wires2) # or wires1 & wires2
Wires([2, 3])

symmetric difference with ^ or symmetric_difference():

>>> wires1.symmetric_difference(wires2) # or wires1 ^ wires2
Wires([1, 4])

union with | or union():

>>> wires1.union(wires2) # or wires1 | wires2
Wires([1, 2, 3, 4])

difference with - or difference():

>>> wires1.difference(wires2) # or wires1 - wires2
Wires([1])

Quantum arithmetic operations 🧮

Several new operator templates have been added to PennyLane that let you perform quantum arithmetic operations. (#6109) (#6112) (#6121)
- qml.Adder performs in-place modular addition: $\text{Adder}(k, m)\vert x \rangle = \vert x + k ; \text{mod} ; m\rangle$.
- qml.PhaseAdder is similar to qml.Adder, but it performs in-place modular addition in the Fourier basis.
- qml.Multiplier performs in-place multiplication: $\text{Multiplier}(k, m)\vert x \rangle = \vert x \times k ; \text{mod} ; m \rangle$.
- qml.OutAdder performs out-place modular addition: $\text{OutAdder}(m)\vert x \rangle \vert y \rangle \vert b \rangle = \vert x \rangle \vert y \rangle \vert b + x + y ; \text{mod} ; m \rangle$.
- qml.OutMultiplier performs out-place modular multiplication: $\text{OutMultiplier}(m)\vert x \rangle \vert y \rangle \vert b \rangle = \vert x \rangle \vert y \rangle \vert b + x \times y ; \text{mod} ; m \rangle$.
- qml.ModExp performs modular exponentiation: $\text{ModExp}(base, m) \vert x \rangle \vert k \rangle = \vert x \rangle \vert k \times base^x ; \text{mod} ; m \rangle$.
Here is a comprehensive example that performs the following calculation: (2 + 1) * 3 mod 7 = 2 (or 010 in binary).
```
dev = qml.device("default.qubit", shots=1)

wire_reg = qml.registers({
    "x_wires": 2, # |x>: stores the result of 2 + 1 = 3
    "y_wires": 2, # |y>: multiples x by 3
    "output_wires": 3, # stores the result of (2 + 1) * 3 m 7 = 2
    "work_wires": 2 # for qml.OutMultiplier
})

@qml.qnode(dev)
def circuit():
    # In-place addition
    qml.BasisEmbedding(2, wires=wire_reg["x_wires"])
    qml.Adder(1, x_wires=wire_reg["x_wires"]) # add 1 to wires [0, 1] 

    # Out-place multiplication
    qml.BasisEmbedding(3, wires=wire_reg["y_wires"])
    qml.OutMultiplier(
        wire_reg["x_wires"], 
        wire_reg["y_wires"], 
        wire_reg["output_wires"], 
        work_wires=wire_reg["work_wires"], 
        mod=7
    ) 

    return qml.sample(wires=wire_reg["output_wires"])
```
```
>>> circuit()
array([0, 1, 0])
```

Converting noise models from Qiskit ♻️

Convert Qiskit noise models into a PennyLane NoiseModel with qml.from_qiskit_noise. (#5996)

In the last few releases, we've added substantial improvements and new features to the Pennylane-Qiskit plugin. With this release, a new qml.from_qiskit_noise function allows you to convert a Qiskit noise model into a PennyLane NoiseModel. Here is a simple example with two quantum errors that add two different depolarizing errors based on the presence of different gates in the circuit:
```
import pennylane as qml
import qiskit_aer.noise as noise

error_1 = noise.depolarizing_error(0.001, 1) # 1-qubit noise
error_2 = noise.depolarizing_error(0.01, 2) # 2-qubit noise

noise_model = noise.NoiseModel()

noise_model.add_all_qubit_quantum_error(error_1, ['rz', 'ry'])
noise_model.add_all_qubit_quantum_error(error_2, ['cx'])
```
```
>>> qml.from_qiskit_noise(noise_model)
NoiseModel({
  OpIn(['RZ', 'RY']): QubitChannel(num_kraus=4, num_wires=1)
  OpIn(['CNOT']): QubitChannel(num_kraus=16, num_wires=2)
})
```
Under the hood, PennyLane converts each quantum error in the Qiskit noise model into an equivalent qml.QubitChannel operator with the same canonical Kraus representation. Currently, noise models in PennyLane do not support readout errors. As such, those will be skipped during conversion if they are present in the Qiskit noise model.

Make sure to pip install pennylane-qiskit to access this new feature!

Substantial upgrades to mid-circuit measurements using tree-traversal 🌳

The "tree-traversal" algorithm for mid-circuit measurements (MCMs) on default.qubit has been internally redesigned for better performance. (#5868)

In the last release (v0.37), we introduced the tree-traversal MCM method, which was implemented in a recursive way for simplicity. However, this had the unintended consequence of very deep stack calls for circuits with many MCMs, resulting in stack overflows in some cases. With this release, we've refactored the implementation of the tree-traversal method into an iterative approach, which solves those inefficiencies when many MCMs are present in a circuit.

The tree-traversal algorithm is now compatible with analytic-mode execution (shots=None). (#5868)

dev = qml.device("default.qubit")

n_qubits = 5

@qml.qnode(dev, mcm_method="tree-traversal")
def circuit():
    for w in range(n_qubits):
        qml.Hadamard(w)
    
    for w in range(n_qubits - 1):
        qml.CNOT(wires=[w, w+1])

    for w in range(n_qubits):
        m = qml.measure(w)
        qml.cond(m == 1, qml.RX)(0.1967 * (w + 1), w)

    return [qml.expval(qml.Z(w)) for w in range(n_qubits)]

>>> circuit()
[tensor(0.00964158, requires_grad=True),
 tensor(0.03819446, requires_grad=True),
 tensor(0.08455748, requires_grad=True),
 tensor(0.14694258, requires_grad=True),
 tensor(0.2229438, requires_grad=True)]

Improvements 🛠

Creating spin Hamiltonians

Three new functions are now available for creating commonly-used spin Hamiltonians in PennyLane: (#6106) (#6128)
- qml.spin.transverse_ising creates the transverse-field Ising model Hamiltonian.
- qml.spin.heisenberg creates the Heisenberg model Hamiltonian.
- qml.spin.fermi_hubbard creates the [Fermi...

Assets 2

08 Jul 22:37

astralcai

v0.37.0

af5bd6d

Release 0.37.0

New features since last release

Execute wide circuits with Default Tensor 🔗

A new default.tensor device is now available for performing tensor network and matrix product state simulations of quantum circuits using the quimb backend. (#5699) (#5744) (#5786) (#5795)

Either method can be selected when instantiating the default.tensor device by setting the method keyword argument to "tn" (tensor network) or "mps" (matrix product state).

There are several templates in PennyLane that are tensor-network focused, which are excellent candidates for the "tn" method for default.tensor. The following example shows how a circuit comprising gates in a tree tensor network architecture can be efficiently simulated using method="tn".

import pennylane as qml

n_wires = 16
dev = qml.device("default.tensor", method="tn")

def block(weights, wires):
    qml.CNOT(wires=[wires[0], wires[1]])
    qml.RY(weights[0], wires=wires[0])
    qml.RY(weights[1], wires=wires[1])

n_block_wires = 2
n_params_block = 2
n_blocks = qml.TTN.get_n_blocks(range(n_wires), n_block_wires)
template_weights = [[0.1, -0.3]] * n_blocks

@qml.qnode(dev)
def circuit(template_weights):
    for i in range(n_wires):
        qml.Hadamard(i)
    qml.TTN(range(n_wires), n_block_wires, block, n_params_block, template_weights)
    return qml.expval(qml.Z(n_wires - 1))

>>> circuit(template_weights)
0.3839174759751649

For matrix product state simulations (method="mps"), we can make the execution be approximate by setting max_bond_dim (see the device's documentation for more details). The maximum bond dimension has implications for the speed of the simulation and lets us control the degree of the approximation, as shown in the following example. First, set up the circuit:

import numpy as np

n_layers = 10 
n_wires = 10
initial_shape, weights_shape = qml.SimplifiedTwoDesign.shape(n_layers, n_wires) 
np.random.seed(1967) 
initial_layer_weights = np.random.random(initial_shape) 
weights = np.random.random(weights_shape)

def f(): 
    qml.SimplifiedTwoDesign(initial_layer_weights, weights, range(n_wires)) 
    return qml.expval(qml.Z(0))

The default.tensor device is instantiated with a max_bond_dim value:

dev_dq = qml.device("default.qubit") 
value_dq = qml.QNode(f, dev_dq)()

dev_mps = qml.device("default.tensor", max_bond_dim=5) 
value_mps = qml.QNode(f, dev_mps)()

With this bond dimension, the expectation values calculated for default.qubit and default.tensor are different:

>>> np.abs(value_dq - value_mps) 
tensor(0.0253213, requires_grad=True)

Learn more about default.tensor and how to configure it by visiting the how-to guide.

Add noise models to your quantum circuits 📺

Support for building noise models and applying them to a quantum circuit has been added via the NoiseModel class and an add_noise transform. (#5674) (#5684) (#5718)

Under the hood, PennyLane's approach to noise models is insertion-based, meaning that noise is included by inserting additional operators (gates or channels) that describe the noise into the quantum circuit. Creating a NoiseModel boils down to defining Boolean conditions under which specific noisy operations are inserted. There are several ways to specify conditions for adding noisy operations:
- qml.noise.op_eq(op): if the operator op is encountered in the circuit, add noise.
- qml.noise.op_in(ops): if any operators in ops are encountered in the circuit, add noise.
- qml.noise.wires_eq(wires): if an operator is applied to wires, add noise.
- qml.noise.wires_in(wires): if an operator is applied to any wire in wires, add noise.
- custom noise conditions: custom conditions can be defined as functions decorated with qml.BooleanFn that return a Boolean value. For example, the following function will insert noise if a qml.RY operator is encountered with an angle of rotation that is less than 0.5:
```
@qml.BooleanFn 
def c0(op): 
    return isinstance(op, qml.RY) and op.parameters[0] < 0.5 
```
Conditions can also be combined together with &, and, |, etc. Once the conditions under which noise is to be inserted have been stated, we can specify exactly what noise is inserted with the following:
- qml.noise.partial_wires(op): insert op on the wires that are specified by the condition that triggers adding this noise
- custom noise operations: custom noise can be specified by defining a standard quantum function like below.
```
def n0(op, **kwargs): 
    qml.RY(op.parameters[0] * 0.05, wires=op.wires) 
```
With that, we can create a qml.NoiseModel object whose argument must be a dictionary mapping conditions to noise:
```
c1 = qml.noise.op_eq(qml.X) & qml.noise.wires_in([0, 1]) 
n1 = qml.noise.partial_wires(qml.AmplitudeDamping, 0.4)

noise_model = qml.NoiseModel({c0: n0, c1: n1}) 
```
```
>>> noise_model 
NoiseModel({ BooleanFn(c0): n0 OpEq(PauliX) | WiresIn([0, 1]): AmplitudeDamping(gamma=0.4) }) 
```
The noise model created can then be added to a QNode with qml.add_noise:
```
dev = qml.device("lightning.qubit", wires=3)

@qml.qnode(dev) 
def circuit(): 
    qml.Y(0) 
    qml.CNOT([0, 1]) 
    qml.RY(0.3, wires=2) # triggers c0 
    qml.X(1) # triggers c1 
    return qml.state() 
```
```
>>> print(qml.draw(circuit)()) 
0: ──Y────────╭●────┤ State 
1: ───────────╰X──X─┤ State 
2: ──RY(0.30)───────┤ State 
>>> circuit = qml.add_noise(circuit, noise_model) 
>>> print(qml.draw(circuit)()) 
0: ──Y────────╭●───────────────────────────────────┤ State 
1: ───────────╰X─────────X──AmplitudeDamping(0.40)─┤ State 
2: ──RY(0.30)──RY(0.01)────────────────────────────┤ State 
```
If more than one transform is applied to a QNode, control over when/where the add_noise transform is applied in relation to the other transforms can be specified with the level keyword argument. By default, add_noise is applied after all the transforms that have been manually applied to the QNode until that point. To learn more about this new functionality, check out our noise module documentation and keep your eyes peeled for an in-depth demo!

Catch bugs with the PennyLane debugger 🚫🐞

The new PennyLane quantum debugger allows pausing simulation via the qml.breakpoint() command and provides tools for analyzing quantum circuits during execution. (#5680) (#5749) (#5789)

This includes monitoring the circuit via measurements using qml.debug_state(), qml.debug_probs(), qml.debug_expval(), and qml.debug_tape(), stepping through the operations in a quantum circuit, and interactively adding operations during execution.

Including qml.breakpoint() in a circuit will cause the simulation to pause during execution and bring up the interactive console. For example, consider the following code in a Python file called script.py:
```
@qml.qnode(qml.device('default.qubit', wires=(0,1,2))) 
def circuit(x): 
    qml.Hadamard(wires=0) 
    qml.CNOT(wires=(0,2)) 
    qml.breakpoint()

    qml.RX(x, wires=1) 
    qml.RY(x, wires=2) 
    qml.breakpoint()

    return qml.sample()

circuit(1.2345) 
```
Upon executing script.py, the simulation pauses at the first breakpoint:
```
> /Users/your/path/to/script.py(8)circuit()
-> qml.RX(x, wires=1) 
[pldb] 
```
While debugging, we can access circuit information. For example, qml.debug_tape() returns the tape of the circuit, giving access to its operations and drawing:
```
[pldb] tape = qml.debug_tape() 
[pldb] print(tape.draw(wire_order=[0,1,2])) 
0: ──H─╭●─┤ 
2: ────╰X─┤ 
[pldb] tape.operations 
[Hadamard(wires=[0]), CNOT(wires=[0, 2])] 
```
While qml.debug_state() is equivalent to qml.state() and gives the current state:
```
[pldb] print(qml.debug_state()) 
[0.70710678+0.j 0. +0.j 0. +0.j 0. +0.j 1. +0.j 0.70710678+0.j 0. +0.j 0. +0.j] 
```
Other debugger functions like qml.debug_probs() and qml.debug_expval() also function like their simulation counterparts (qml.probs and qml.expval, respectively) and are described in more detail in the debugger documentation Additionally, standard debugging commands are available to navigate through code, including list, longlist, next, continue, and quit, as described in [the debugging documentation](https://docs.pennylane....

Assets 2

06 May 22:02

astralcai

v0.36.0

6d80d25

Release 0.36.0

New features since last release

Estimate errors in a quantum circuit 🧮

This version of PennyLane lays the foundation for estimating the total error in a quantum circuit from the combination of individual gate errors. (#5154) (#5464) (#5465) (#5278) (#5384)

Two new user-facing classes enable calculating and propagating gate errors in PennyLane:

qml.resource.SpectralNormError: the spectral norm error is defined as the distance, in spectral norm, between the true unitary we intend to apply and the approximate unitary that is actually applied.
qml.resource.ErrorOperation: a base class that inherits from qml.operation.Operation and represents quantum operations which carry some form of algorithmic error.

SpectralNormError can be used for back-of-the-envelope type calculations like obtaining the spectral norm error between two unitaries via get_error:
```
import pennylane as qml 
from pennylane.resource import ErrorOperation, SpectralNormError

intended_op = qml.RY(0.40, 0) 
actual_op = qml.RY(0.41, 0) # angle of rotation is slightly off
```
```
>>> SpectralNormError.get_error(intended_op, actual_op) 
0.004999994791668309 
```
SpectralNormError is also a key tool to specify errors in larger quantum circuits:
For operations representing a major building block of an algorithm, we can create a custom operation that inherits from ErrorOperation. This child class must override the error method and should return a SpectralNormError instance:
```
class MyErrorOperation(ErrorOperation):
   
   def __init__(self, error_val, wires): 
       self.error_val = error_val 
       super().__init__(wires=wires)

   def error(self): 
       return SpectralNormError(self.error_val)
```
In this toy example, MyErrorOperation introduces an arbitrary SpectralNormError when called in a QNode. It does not require a decomposition or matrix representation when used with null.qubit (suggested for use with resource and error estimation since circuit executions are not required to calculate resources or errors).
```
dev = qml.device("null.qubit")

@qml.qnode(dev) 
def circuit(): 
   MyErrorOperation(0.1, wires=0) 
   MyErrorOperation(0.2, wires=1) 
   return qml.state() 
```
The total spectral norm error of the circuit can be calculated using qml.specs:
```
>>> qml.specs(circuit)()['errors'] 
{'SpectralNormError': SpectralNormError(0.30000000000000004)} 
```
PennyLane already includes a number of built-in building blocks for algorithms like QuantumPhaseEstimation and TrotterProduct. TrotterProduct now propagates errors based on the number of steps performed in the Trotter product. QuantumPhaseEstimation now propagates errors based on the error of its input unitary.
```
dev = qml.device('null.qubit') 
hamiltonian = qml.dot([1.0, 0.5, -0.25], [qml.X(0), qml.Y(0), qml.Z(0)])

@qml.qnode(dev) 
def circuit(): 
   qml.TrotterProduct(hamiltonian, time=0.1, order=2) 
   qml.QuantumPhaseEstimation(MyErrorOperation(0.01, wires=0), estimation_wires=[1, 2, 3]) 
   return qml.state()
```
Again, the total spectral norm error of the circuit can be calculated using qml.specs:
```
>>> qml.specs(circuit)()["errors"] 
{'SpectralNormError': SpectralNormError(0.07616666666666666)} 
```
Check out our error propagation demo to see how to use these new features in a real-world example!

Access an extended arsenal of quantum algorithms 🏹

The Fast Approximate BLock-Encodings (FABLE) algorithm for embedding a matrix into a quantum circuit as outlined in arXiv:2205.00081 is now accessible via the qml.FABLE template. (#5107)

The usage of qml.FABLE is similar to qml.BlockEncode but provides a more efficient circuit construction at the cost of a user-defined approximation level, tol. The number of wires that qml.FABLE operates on is 2*n + 1, where n defines the dimension of the $2^n \times 2^n$ matrix that we want to block-encode.
```
import numpy as np

A = np.array([[0.1, 0.2], [0.3, 0.4]]) 
dev = qml.device('default.qubit', wires=3)

@qml.qnode(dev) 
def circuit(): 
   qml.FABLE(A, tol = 0.001, wires=range(3)) 
   return qml.state() 
```
```
>>> mat = qml.matrix(circuit)() 
>>> 2 * mat[0:2, 0:2] 
array([[0.1+0.j, 0.2+0.j], [0.3+0.j, 0.4+0.j]]) 
```
A high-level interface for amplitude amplification and its variants is now available via the new qml.AmplitudeAmplification template. (#5160)

Based on arXiv:quant-ph/0005055, given a state $\vert \Psi \rangle = \alpha \vert \phi \rangle + \beta \vert \phi^{\perp} \rangle$, qml.AmplitudeAmplification amplifies the amplitude of $\vert \phi \rangle$.

Here's an example with a target state $\vert \phi \rangle = \vert 2 \rangle = \vert 010 \rangle$, an input state $\vert \Psi \rangle = H^{\otimes 3} \vert 000 \rangle$, as well as an oracle that flips the sign of $\vert \phi \rangle$ and does nothing to $\vert \phi^{\perp} \rangle$, which can be achieved in this case through qml.FlipSign.
```
@qml.prod 
def generator(wires): 
   for wire in wires: 
       qml.Hadamard(wires=wire)

U = generator(wires=range(3)) 
O = qml.FlipSign(2, wires=range(3)) 
```
Here, U is a quantum operation that is created by decorating a quantum function with @qml.prod. This could alternatively be done by creating a user-defined custom operation with a decomposition. Amplitude amplification can then be set up within a circuit:
```
dev = qml.device("default.qubit")

@qml.qnode(dev) 
def circuit(): 
   generator(wires=range(3)) # prepares |Psi> = U|0> 
   qml.AmplitudeAmplification(U, O, iters=10)
   return qml.probs(wires=range(3)) 
```
```
>>> print(np.round(circuit(), 3)) 
[0.01 0.01 0.931 0.01 0.01 0.01 0.01 0.01 ] 
```
As expected, we amplify the $\vert 2 \rangle$ state.
Reflecting about a given quantum state is now available via qml.Reflection. This operation is very useful in the amplitude amplification algorithm and offers a generalization of qml.FlipSign, which operates on basis states. (#5159)

qml.Reflection works by providing an operation, $U$, that prepares the desired state, $\vert \psi \rangle$, that we want to reflect about. In other words, $U$ is such that $U \vert 0 \rangle = \vert \psi \rangle$. In PennyLane, $U$ must be an Operator. For example, if we want to reflect about $\vert \psi \rangle = \vert + \rangle$, then $U = H$:
```
U = qml.Hadamard(wires=0)
dev = qml.device('default.qubit') 

@qml.qnode(dev) 
def circuit(): 
   qml.Reflection(U) 
   return qml.state() 
```
```
>>> circuit() 
tensor([0.-6.123234e-17j, 1.+6.123234e-17j], requires_grad=True) 
```

Performing qubitization is now easily accessible with the new qml.Qubitization operator. (#5500)

qml.Qubitization encodes a Hamiltonian into a suitable unitary operator. When applied in conjunction with quantum phase estimation (QPE), it allows for computing the eigenvalue of an eigenvector of the given Hamiltonian.

H = qml.dot([0.1, 0.3, -0.3], [qml.Z(0), qml.Z(1), qml.Z(0) @ qml.Z(2)]) 
@qml.qnode(qml.device("default.qubit")) 
def circuit(): 
   # initialize the eigenvector 
   qml.PauliX(2) 
   # apply QPE 
   measurements = qml.iterative_qpe(
       qml.Qubitization(H, control = [3,4]), ancilla = 5, iters = 3
   ) 
   return qml.probs(op = measurements)

Make use of more methods to map from molecules 🗺️

A new function called qml.bravyi_kitaev has been added to perform the Bravyi-Kitaev mapping of fermionic Hamiltonians to qubit Hamiltonians. (#5390)

This function presents an alternative mapping to qml.jordan_wigner or qml.parity_transform which can help us measure expectation values more efficiently on hardware. Simply provide a fermionic Hamiltonian (created from from_string, FermiA, FermiC, FermiSentence, or FermiWord) and the number of qubits / spin orbitals in the system, n:
```
>>> fermi_ham = qml.fermi.from_string('0+ 1+ 1- 0-') 
>>> qubit_ham = qml.bravyi_kitaev(fermi_ham, n=6, tol=0.0) 
>>> print(qubit_ham) 
0.25 * I(0) + -0.25 * Z(0) + -0.25 * (Z(0) @ Z(1)) + 0.25 * Z(1) 
```
The qml.qchem.hf_state function has been upgraded to be compatible with qml.parity_transform and the new Bravyi-Kitaev mapping (qml.bravyi_kitaev). (#5472) (#5472)
```
>>> state_bk = qml.qchem.hf_state(2, 6, basis="bravyi_kitaev") 
>>> print(state_bk) 
[1 0 0 ...
```

Assets 2

11 Mar 21:09

Mandrenkov

v0.35.1

db2fb6d

Release 0.35.1

Bug fixes 🐛

Lightning simulators need special handling of diagonalizing gates when performing sampling measurements. (#5343)
Updated the lower bound on the required Catalyst version to v0.5.0. (#5320)

Contributors ✍️

This release contains contributions from (in alphabetical order):

Vincent Michaud-Rioux, Erick Ochoa Lopez.

Assets 2

04 Mar 20:25

lillian542

v0.35.0

cf042f6

Release 0.35.0

New features since last release

Qiskit 1.0 integration 🔌

This version of PennyLane makes it easier to import circuits from Qiskit. (#5218) (#5168)

The qml.from_qiskit function converts a Qiskit QuantumCircuit into a PennyLane quantum function. Although qml.from_qiskit already exists in PennyLane, we have made a number of improvements to make importing from Qiskit easier. And yes — qml.from_qiskit functionality is compatible with both Qiskit 1.0 and earlier versions! Here's a comprehensive list of the improvements:

You can now append PennyLane measurements onto the quantum function returned by qml.from_qiskit. Consider this simple Qiskit circuit:

import pennylane as qml 
from qiskit import QuantumCircuit

qc = QuantumCircuit(2) 
qc.rx(0.785, 0) 
qc.ry(1.57, 1)

We can convert it into a PennyLane QNode in just a few lines, with PennyLane measurements easily included:

>>> dev = qml.device("default.qubit") 
>>> measurements = qml.expval(qml.Z(0) @ qml.Z(1)) 
>>> qfunc = qml.from_qiskit(qc, measurements=measurements) 
>>> qnode = qml.QNode(qfunc, dev) 
>>> qnode() 
tensor(0.00056331, requires_grad=True)

Quantum circuits that already contain Qiskit-side measurements can be faithfully converted with qml.from_qiskit. Consider this example Qiskit circuit:

qc = QuantumCircuit(3, 2) # Teleportation

qc.rx(0.9, 0) # Prepare input state on qubit 0

qc.h(1) # Prepare Bell state on qubits 1 and 2 qc.cx(1, 2)

qc.cx(0, 1) # Perform teleportation 
qc.h(0) 
qc.measure(0, 0) 
qc.measure(1, 1)

with qc.if_test((1, 1)): # Perform first conditional 
    qc.x(2)

This circuit can be converted into PennyLane with the Qiskit measurements still accessible. For example, we can use those results as inputs to a mid-circuit measurement in PennyLane:

@qml.qnode(dev) 
def teleport(): 
    m0, m1 = qml.from_qiskit(qc)() 
    qml.cond(m0, qml.Z)(2) 
    return qml.density_matrix(2)

>>> teleport() 
tensor([[0.81080498+0.j , 0. +0.39166345j], 
[0. -0.39166345j, 0.18919502+0.j ]], requires_grad=True)

It is now more intuitive to handle and differentiate parametrized Qiskit circuits. Consider the following circuit:

from qiskit.circuit import Parameter 
from pennylane import numpy as np

angle0 = Parameter("x") angle1 = Parameter("y")

qc = QuantumCircuit(2, 2) 
qc.rx(angle0, 0) 
qc.ry(angle1, 1) 
qc.cx(1, 0)

We can convert this circuit into a QNode with two arguments, corresponding to x and y:

measurements = qml.expval(qml.PauliZ(0)) 
qfunc = qml.from_qiskit(qc, measurements) 
qnode = qml.QNode(qfunc, dev)

The QNode can be evaluated and differentiated:

>>> x, y = np.array([0.4, 0.5], requires_grad=True) 
>>> qnode(x, y) 
tensor(0.80830707, requires_grad=True) 

>>> qml.grad(qnode)(x, y) 
(tensor(-0.34174675, requires_grad=True), tensor(-0.44158016, requires_grad=True))

This shows how easy it is to make a Qiskit circuit differentiable with PennyLane.

In addition to circuits, it is also possible to convert operators from Qiskit to PennyLane with a new function called qml.from_qiskit_op. (#5251)

A Qiskit SparsePauliOp can be converted to a PennyLane operator using qml.from_qiskit_op:

>>> from qiskit.quantum_info import SparsePauliOp 
>>> qiskit_op = SparsePauliOp(["II", "XY"]) 
>>> qiskit_op SparsePauliOp(['II', 'XY'], coeffs=[1.+0.j, 1.+0.j]) 
>>> pl_op = qml.from_qiskit_op(qiskit_op) 
>>> pl_op I(0) + X(1) @ Y(0)

Combined with qml.from_qiskit, it becomes easy to quickly calculate quantities like expectation values by converting the whole workflow to PennyLane:

qc = QuantumCircuit(2) # Create circuit 
qc.rx(0.785, 0) 
qc.ry(1.57, 1)

measurements = qml.expval(pl_op) # Create QNode 
qfunc = qml.from_qiskit(qc, measurements) 
qnode = qml.QNode(qfunc, dev)

>>> qnode() # Evaluate! 
tensor(0.29317504, requires_grad=True)

Native mid-circuit measurements on Default Qubit 💡

Mid-circuit measurements can now be more scalable and efficient in finite-shots mode with default.qubit by simulating them in a similar way to what happens on quantum hardware. (#5088) (#5120)

Previously, mid-circuit measurements (MCMs) would be automatically replaced with an additional qubit using the @qml.defer_measurements transform. The circuit below would have required thousands of qubits to simulate.

Now, MCMs are performed in a similar way to quantum hardware with finite shots on default.qubit. For each shot and each time an MCM is encountered, the device evaluates the probability of projecting onto |0> or |1> and makes a random choice to collapse the circuit state. This approach works well when there are a lot of MCMs and the number of shots is not too high.
```
import pennylane as qml

dev = qml.device("default.qubit", shots=10)

@qml.qnode(dev) 
def f(): 
    for i in range(1967): 
        qml.Hadamard(0) 
        qml.measure(0) 
    return qml.sample(qml.PauliX(0)) 
```
```
>>> f() 
tensor([-1, -1, -1, 1, 1, -1, 1, -1, 1, -1], requires_grad=True) 
```

Work easily and efficiently with operators 🔧

Over the past few releases, PennyLane's approach to operator arithmetic has been in the process of being overhauled. We have a few objectives:
1. To make it as easy to work with PennyLane operators as it would be with pen and paper.
2. To improve the efficiency of operator arithmetic.
The updated operator arithmetic functionality is still being finalized, but can be activated using qml.operation.enable_new_opmath(). In the next release, the new behaviour will become the default, so we recommend enabling now to become familiar with the new system!

The following updates have been made in this version of PennyLane:
- You can now easily access Pauli operators via I, X, Y, and Z: (#5116)
```
>>> from pennylane import I, X, Y, Z 
>>> X(0) X(0) ```

The original long-form names `Identity`, `PauliX`, `PauliY`, and `PauliZ` remain available, but use of the short-form names is now recommended.
```
- A new qml.commutator function is now available that allows you to compute commutators between PennyLane operators. (#5051) (#5052) (#5098)
```
>>> qml.commutator(X(0), Y(0)) 
2j * Z(0) 
```
- Operators in PennyLane can have a backend Pauli representation, which can be used to perform faster operator arithmetic. Now, the Pauli representation will be automatically used for calculations when available. (#4989) (#5001) (#5003) (#5017) (#5027)
  
  The Pauli representation can be optionally accessed via op.pauli_rep:
```
>>> qml.operation.enable_new_opmath() 
>>> op = X(0) + Y(0) 
>>> op.pauli_rep 
1.0 * X(0) + 1.0 * Y(0) 
```
- Extensive improvements have been made to the string representations of PennyLane operators, making them shorter and possible to copy-paste as valid PennyLane code. (#5116) (#5138)
```
>>> 0.5 * X(0) 
0.5 * X(0)
>>> 0.5 * (X(0) + Y(1)) 
0.5 * (X(0) + Y(1)) 
```
  Sums with many terms are broken up into multiple lines, but can still be copied back as valid code:
```
>>> 0.5 * (X(0) @ X(1)) + 0.7 * (X(1) @ X(2)) + 0.8 * (X(2) @ X(3)) 
( 
     0.5 * (X(0) @ X(1)) 
     + 0.7 * (X(1) @ X(2)) 
     + 0.8 * (X(2) @ X(3)) 
) 
```
- Linear combinations of operators and operator multiplication via Sum and Prod, respectively, have been updated to reach feature parity with Hamiltonian and Tensor, respectively. This should minimize the effort to port over any existing code. (#5070) (#5132) (#5133)
  
  Updates include support for grouping via the pauli module:
```
>>> obs = [X(0) @ Y(1), Z(0), Y(0) @ Z(1), Y(1)] 
>>> qml.pauli.group_observables(obs) 
[[Y(0) @ Z(1)], [X(0) @ Y(1), Y(1)], [Z(0)]] 
```

New Clifford device 🦾

A new default.clifford device enables efficient simulati...

Assets 3

22 Jan 17:04

albi3ro

v0.34.0.post1

11ca3ee

Release 0.34.0.post1

This postfix release pins additional requirements in doc/requirements.txt for building the website documentation. This allows the website to be rebuilt to show the "Getting involved" section.

Assets 2

08 Jan 20:06

lillian542

v0.34.0

1a315b9

Release 0.34.0

New features since last release

Statistics and drawing for mid-circuit measurements 🎨

It is now possible to return statistics of composite mid-circuit measurements. (#4888)

Mid-circuit measurement results can be composed using basic arithmetic operations and then statistics can be calculated by putting the result within a PennyLane measurement like qml.expval(). For example:

import pennylane as qml

dev = qml.device("default.qubit")

@qml.qnode(dev) 
def circuit(phi, theta): 
    qml.RX(phi, wires=0) 
    m0 = qml.measure(wires=0) 
    qml.RY(theta, wires=1) 
    m1 = qml.measure(wires=1) 
    return qml.expval(~m0 + m1)

print(circuit(1.23, 4.56))

1.2430187928114291

Another option, for ease-of-use when using qml.sample(), qml.probs(), or qml.counts(), is to provide a simple list of mid-circuit measurement results:

dev = qml.device("default.qubit")

@qml.qnode(dev) 
def circuit(phi, theta): 
    qml.RX(phi, wires=0) 
    m0 = qml.measure(wires=0) 
    qml.RY(theta, wires=1) 
    m1 = qml.measure(wires=1) 
    return qml.sample(op=[m0, m1])

print(circuit(1.23, 4.56, shots=5))

[[0 1] 
 [0 1] 
 [0 0] 
 [1 0] 
 [0 1]]

Composite mid-circuit measurement statistics are supported on default.qubit and default.mixed. To learn more about which measurements and arithmetic operators are supported, refer to the measurements page and the documentation for qml.measure.

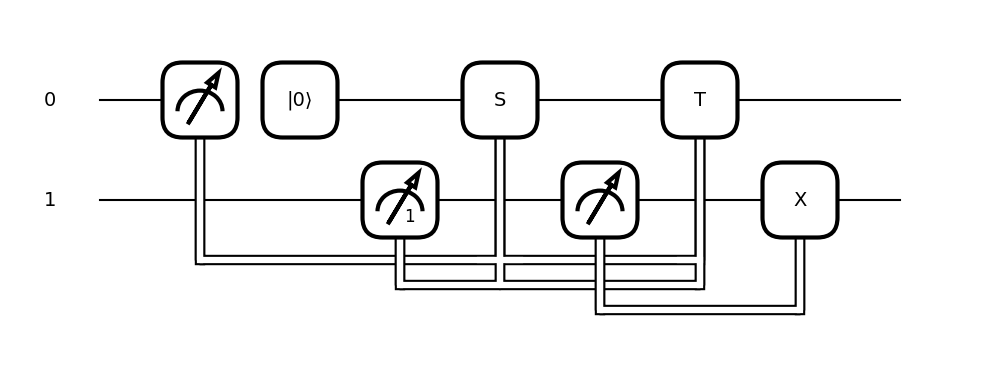
Mid-circuit measurements can now be visualized with the text-based qml.draw() and the graphical qml.draw_mpl() methods. (#4775) (#4803) (#4832) (#4901) (#4850) (#4917) (#4930) (#4957)

Drawing of mid-circuit measurement capabilities including qubit reuse and reset, postselection, conditioning, and collecting statistics is now supported. Here is an all-encompassing example:

def circuit(): 
    m0 = qml.measure(0, reset=True) 
    m1 = qml.measure(1, postselect=1) 
    qml.cond(m0 - m1 == 0, qml.S)(0) 
    m2 = qml.measure(1) 
    qml.cond(m0 + m1 == 2, qml.T)(0) 
    qml.cond(m2, qml.PauliX)(1)

The text-based drawer outputs:

>>> print(qml.draw(circuit)()) 
0: ──┤↗│  │0⟩────────S───────T────┤ 
1: ───║────────┤↗₁├──║──┤↗├──║──X─┤ 
      ╚═════════║════╬═══║═══╣  ║ 
                ╚════╩═══║═══╝  ║ 
                         ╚══════╝

The graphical drawer outputs:

>>> print(qml.draw_mpl(circuit)())

Catalyst is seamlessly integrated with PennyLane ⚗️

Catalyst, our next-generation compilation framework, is now accessible within PennyLane, allowing you to more easily benefit from hybrid just-in-time (JIT) compilation.

To access these features, simply install pennylane-catalyst:
```
pip install pennylane-catalyst 
```
The qml.compiler module provides support for hybrid quantum-classical compilation. (#4692) (#4979)

Through the use of the qml.qjit decorator, entire workflows can be JIT compiled — including both quantum and classical processing — down to a machine binary on first-function execution. Subsequent calls to the compiled function will execute the previously-compiled binary, resulting in significant performance improvements.
```
import pennylane as qml

dev = qml.device("lightning.qubit", wires=2)

@qml.qjit 
@qml.qnode(dev) 
def circuit(theta): 
    qml.Hadamard(wires=0) 
    qml.RX(theta, wires=1) 
    qml.CNOT(wires=[0,1]) 
    return qml.expval(qml.PauliZ(wires=1)) 
```
```
>>> circuit(0.5) # the first call, compilation occurs here array(0.) 
>>> circuit(0.5) # the precompiled quantum function is called 
array(0.) 
```
Currently, PennyLane supports the Catalyst hybrid compiler with the qml.qjit decorator. A significant benefit of Catalyst is the ability to preserve complex control flow around quantum operations — such as if statements and for loops, and including measurement feedback — during compilation, while continuing to support end-to-end autodifferentiation.

The following functions can now be used with the qml.qjit decorator: qml.grad, qml.jacobian, qml.vjp, qml.jvp, and qml.adjoint. (#4709) (#4724) (#4725) (#4726)

When qml.grad or qml.jacobian are used with @qml.qjit, they are patched to catalyst.grad and catalyst.jacobian, respectively.

dev = qml.device("lightning.qubit", wires=1)

@qml.qjit 
def workflow(x):

    @qml.qnode(dev) 
    def circuit(x): 
        qml.RX(np.pi * x[0], wires=0) 
        qml.RY(x[1], wires=0) 
        return qml.probs()

    g = qml.jacobian(circuit)

    return g(x)

>>> workflow(np.array([2.0, 1.0])) 
array([[ 3.48786850e-16, -4.20735492e-01], 
       [-8.71967125e-17, 4.20735492e-01]])

JIT-compatible functionality for control flow has been added via qml.for_loop, qml.while_loop, and qml.cond. (#4698)

qml.for_loop and qml.while_loop can be deployed as decorators on functions that are the body of the loop. The arguments to both follow typical conventions:

@qml.for_loop(lower_bound, upper_bound, step)

@qml.while_loop(cond_function)

Here is a concrete example with qml.for_loop:

dev = qml.device("lightning.qubit", wires=1)

@qml.qjit 
@qml.qnode(dev) 
def circuit(n: int, x: float):

    @qml.for_loop(0, n, 1) 
    def loop_rx(i, x): 
        # perform some work and update (some of) the arguments 
        qml.RX(x, wires=0)

        # update the value of x for the next iteration 
        return jnp.sin(x)

    # apply the for loop 
    final_x = loop_rx(x)

    return qml.expval(qml.PauliZ(0)), final_x

>>> circuit(7, 1.6) 
(array(0.97926626), array(0.55395718))

Decompose circuits into the Clifford+T gateset 🧩

The new qml.clifford_t_decomposition() transform provides an approximate breakdown of an input circuit into the Clifford+T gateset. Behind the scenes, this decomposition is enacted via the sk_decomposition() function using the Solovay-Kitaev algorithm. (#4801) (#4802)

The Solovay-Kitaev algorithm approximately decomposes a quantum circuit into the Clifford+T gateset. To account for this, a desired total circuit decomposition error, epsilon, must be specified when using qml.clifford_t_decomposition:

dev = qml.device("default.qubit")

@qml.qnode(dev) 
def circuit(): 
    qml.RX(1.1, 0) 
    return qml.state()

circuit = qml.clifford_t_decomposition(circuit, epsilon=0.1)

>>> print(qml.draw(circuit)()) 
0:   ──T†──H──T†──H──T──H──T──H──T──H──T──H──T†──H──T†──T†──H──T†──H──T──H──T──H──T──H──T──H──T†──H

 ───T†──H──T──H──GlobalPhase(0.39)─┤

The resource requirements of this circuit can also be evaluated:

>>> with qml.Tracker(dev) as tracker: 
...     circuit() 
>>> resources_lst = tracker.history["resources"] 
>>> resources_lst[0] 
wires: 1 
gates: 34 
depth: 34 
shots: Shots(total=None) 
gate_types: {'Adjoint(T)': 8, 'Hadamard': 16, 'T': 9, 'GlobalPhase': 1} 
gate_sizes:   {1: 33, 0: 1}

Use an iterative approach for quantum phase estimation 🔄

Iterative Quantum Phase Estimation is now available with qml.iterative_qpe. (#4804)

The subroutine can be used similarly to mid-circuit measurements:

import pennylane as qml

dev = qml.device("default.qubit", shots=5)

@qml.qnode(dev) 
def circuit():

      # Initial state 
      qml.PauliX(wires=[0])

      # Iterative QPE 
      measurements = qml.iterative_qpe(qml.RZ(2., wires=[0]), ancilla=[1], iters=3)

      return [qml.sample(op=meas) for meas in measurements]

>>> print(circuit()) 
[array([0, 0, 0, 0, 0]), array([1, 0, 0, 0, 0]), array([0, 1, 1, 1...

Assets 2

08 Nov 20:57

timmysilv

v0.33.1

4d9ea4d

Release 0.33.1

Bug fixes 🐛

Fix gradient performance regression due to expansion of VJP products. (#4806)
qml.defer_measurements now correctly transforms circuits when terminal measurements include wires used in mid-circuit measurements. (#4787)
Any ScalarSymbolicOp, like Evolution, now states that it has a matrix if the target is a Hamiltonian. (#4768)
In default.qubit, initial states are now initialized with the simulator's wire order, not the circuit's wire order. (#4781)

Contributors ✍️

This release contains contributions from (in alphabetical order):

Christina Lee, Lee James O'Riordan, Mudit Pandey

Assets 2

Releases: PennyLaneAI/pennylane

Release 0.40.0

New features since last release

Efficient state preparation methods 🦾

Enhanced QSVT functionality 🤩

Generalized Trotter products 🐖

Bosonic operators 🎈

Release 0.39.0

New features since last release

Creating spin Hamiltonians on lattices 💞

Calculating Polynomials 🔢

Readout Noise 📠

User-friendly decompositions 📠

Release 0.38.0

New features since last release

Registers of wires 🧸

Quantum arithmetic operations 🧮

Converting noise models from Qiskit ♻️

Substantial upgrades to mid-circuit measurements using tree-traversal 🌳

Improvements 🛠

Creating spin Hamiltonians

Release 0.37.0

Release 0.37.0

New features since last release

Execute wide circuits with Default Tensor 🔗

Add noise models to your quantum circuits 📺

Catch bugs with the PennyLane debugger 🚫🐞

Release 0.36.0

Release 0.36.0

New features since last release

Estimate errors in a quantum circuit 🧮

Access an extended arsenal of quantum algorithms 🏹

Make use of more methods to map from molecules 🗺️

Release 0.35.1

Bug fixes 🐛

Contributors ✍️

Release 0.35.0

New features since last release

Qiskit 1.0 integration 🔌

Native mid-circuit measurements on Default Qubit 💡

Work easily and efficiently with operators 🔧

New Clifford device 🦾

Release 0.34.0.post1

Release 0.34.0

New features since last release

Statistics and drawing for mid-circuit measurements 🎨

Catalyst is seamlessly integrated with PennyLane ⚗️

Decompose circuits into the Clifford+T gateset 🧩

Use an iterative approach for quantum phase estimation 🔄

Release 0.33.1

Bug fixes 🐛

Contributors ✍️