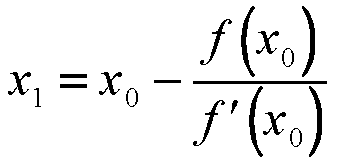Newton-Raphson is a numerical method for solving equations. This program can solve single variable equations in which the terms seperated by addition/subtraction are of form c(x^n)f(x), where f(x)={sin(x), cos(x), tan(x), cot(x), sec(x), cosec(x), log(x), log10(x), exp(x)} and c and n are real numbers, using Newton-Raphson method.
To build this code, CMake needs to be installed on your system. Clone the project on your computer. Open a terminal in the build directory and run the following commands:
cmake ..
cmake --build .
This will generate the executable file in the build folder named newton-raphson.
The input parameters are read from json configurational file "data.json". This file should exist in the same folder as the executable file; which will be inside the build directory, if user follows the above mentioned installation procedure. To read the json file we use nlohmann json library. This aids us in reading the key-value pairs which we then assign to our variables. This file holds the following data:
- maximum number of iterations,
max iterations - the guess solution,
guess solution - tolerance,
tolerance - coefficient vector
coefficient - power vector
power - special function vector
function
Should the coefficient,power and function vectors not be of the same size, the program will throw an error, prompting the user to ensure that the entered data is correct. Same has been done for the max iterations variable, prompting the user to enter a value greater than 0. The vector function takes inteegers from 0-9 corresonpding to a special fucntion each:
- 0: none
- 1: sin(x)
- 2: cos(x)
- 3: tan(x)
- 4: cot(x)
- 5: sec(x)
- 6: cosec(x)
- 7: log(x)
- 8: log10(x)
- 9: exp(x)
The user can choose a 1-9 numbers for a special function or 0 for no function. The current program can only handle equations with terms of the form c*(x^n)*f(x), of which c, n and f(x) are defined as vectors _c, _p and _f respectively in class equation. The class equation in file equation.cpp and equation.h and their methods can be modified to make the code broader in future.
Important Note: Sometimes the value of the differentiated function can become very small or zero, which can lead to huge error or nan (not a number) solution. In such cases, the program will throw a warning and user is should modify the guess solution to get more accurate results.
We solve the polynomial equation x^3*sin(x)-exp(x) using the program. One of the root of the equation is -3.1402.
The user can enter the required input parameters via the data.json file present in the example folder for this case. It is by default copied in the build directory when building the code. Here it should be noted that for a the tolerance value of 0.0001, the user can enter either 1e-4 or 0.0001. Following is the data entered:
{
"data": {
"guess solution": -3,
"tolerance": 1e-5,
"max iterations": 600,
"power": [3,0],
"coefficient": [ 1,-1],
"function": [ 1,9]
}
}
Here the left-hand side is the key used to identify the parameter value on the right-hand side
According to this data, the guess solution, tolerance and maximum number of iterations will be assigned directly. We then ensure that the user has entered positive values for tolerance and maximum number of iterations. Post this we define our function which is to be solved. The corresponding terms in power, coefficient,function relate to the same term in the equation as per the form c*(x^n)*f(x),
where,
c is the coefficient of that particular term in the equation,
n is the power of that x in that particular term in the equation, and
f(x) is the function identifier as per the above described list.
So, for the first term, we get 3 as the power, 1 as the coefficient, and 1 as the function identifier, which constructs the first term as, 1 * x^3 * sin(x). Similarly, the next term is -1*x^0*exp(x).
The program will then print the equation:
You have entered the following equation:
1*x^3*sin(x)+-1*x^0*exp(x)
Now the eq.solve() function will run. It keeps iterating for the solution till convergence criteria is satisfied or maximum number of iterations have been reached using the following equation:
The vector temp from equation.cpp stores the value of the function and value of the differentiated function at a particular x. Then the function solve will iterate until the value of residual drops below the user-defined tolerance OR the maximum number of iterations is reached. Upon occurence of either of these two events, it will present the solution, the number of iterations, and the residual.
The solution is: -3.1402
The number of iterations is: 4
Residual is: 2.81115e-07
The user can add new special functions as required in the file functions.cpp. The user has to add the special function and its derivate in the methods eval and evalDiff respectively and assign a corresonpding number to it in the switch-case structure written in eval and evalDiff methods. The methods eval and evalDiff evaluate the value of the function and its derivate respectively at a given point x. The user also has to modify the range of values user can pass in function in the readData.cpp file from 0-9 to the modified value in the assert() method used to check correct input.