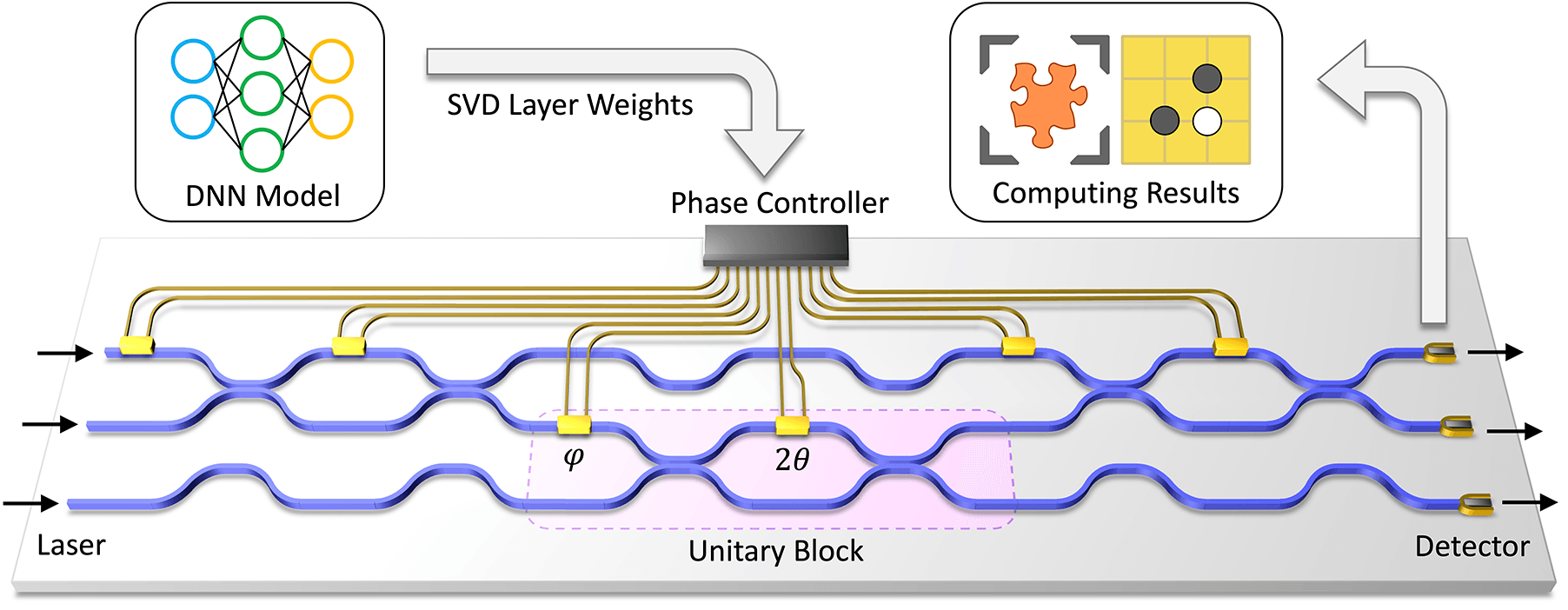
The aim of this project is to create an easy and light-weight libraries of photonic neural networks (PNNs). The current version only includes the models of universal multiport interferometers. We provide Reck's, Clements' and our presented methods in pnn library, which is now available on pypi. The derivation and tutorials can be found in my blog.
You can download the pnn package via pip manager. Copy the command below and paste it onto your terminal. Note that this project is still under development. Once you installed the outdated package, add -U tag and update to the latest version.
pip install pnnThe hierarchy of the project is depicted as follows. Currently pnn comprises two modules: methods and utils.
import pnnIn the utils module, we provide some shortcut functions and classes:
- modified trigonometic functions such as
atan2f,angle_diff; - built-in transfer functions of photonic devices such as
U2BS,U2MZI; - random unitary generator in complex field such as
unitary; - fidelity calculation in terms of a pair of matrices such as
fidelity; - decomposition methods from numpy and scipy such as
svdandcossin.
from pnn.utils import unitary, fidelity, svdIn the methods module, we provide Reck's, Clements' and Yinyi's decomposition methods regarding the matrix mapping of PNN. The functions are wrapped as decompose_<name> and reconstruct_<name>. The details about APIs are listed below:
from pnn.methods import decompose_reck, reconstruct_reck
from pnn.methods import decompose_clements, reconstruct_clements
from pnn.methods import decompose_yinyi, reconstruct_yinyi
# Generate Random Unitary Matrix
u = pnn.utils.unitary(dim=100)
# Decompose by Reck' Method
[phi, theta, alpha] = decompose_reck(u, block='mzi')
Ue = reconstruct_reck(phi, theta, alpha, block='mzi', Lp_dB=0.03, Lc_dB=0.1)
f_clements = fidelity(u, Ue)
# Decompose by Clements' Method
[phi, theta, alpha] = decompose_clements(u, block='mzi')
Ue = reconstruct_clements(phi, theta, alpha, block='mzi', Lp_dB=0.03, Lc_dB=0.1)
f_clements = fidelity(u, Ue)
# Decompose by Yinyi' Method
umi = decompose_yinyi(u, block='mzi', depth=8)
Ue = reconstruct_yinyi(umi, block='mzi', Lp_dB=0.03, Lc_dB=0.1)
f_clements = fidelity(u, Ue)Since Yinyi's is an argumented method over Reck's and Clements' to enable spatial arrangement along the new axis (the direction of plane normal), it supports some distinctive features and APIs:
# Decompose large unitary matrix U
umi = decompose_yinyi(u, block='mzi', depth=0)
# Decompose from the root to the children and the grand children
umi.decompose_recursive(depth=2)
# Decompose from the children matrix to its children individually
umi.u1 = decompose_yinyi(umi.u1, block='bs', depth=1)
umi.u2 = decompose_yinyi(umi.u2, block='mzi', depth=2)
umi.v1h = decompose_yinyi(umi.v1h, block='bs', depth=3)
umi.v2h = decompose_yinyi(umi.v2h, block='mzi', depth=4)
# Obtain and print the children matrix values of umi.u1
print(umi.u1.u1.matrix)
print(umi.u1.u2.matrix)
print(umi.u1.v1h.matrix)
print(umi.u1.v2h.matrix)Please cite the corresponding papers if you find this work useful:
- Yinyi Liu et al. "A Reliability Concern on Photonic Neural Networks." Design, Automation and Test in Europe Conference (DATE). 2022.
- Yinyi Liu et al. "Reduce the Footprints of Multiport Interferometers by Cosine-Sine Decomposition." Optical Fiber Communication (OFC). 2022.