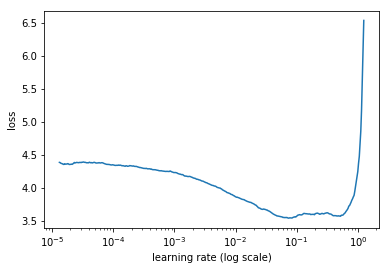
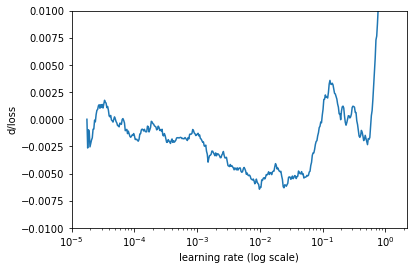
Plots the change of the loss function of a Keras model when the learning rate is exponentially increasing.
See details in "Estimating an Optimal Learning Rate For a Deep Neural Network".
Create and compile a Keras model, then execute this code:
# model is a Keras model
lr_finder = LRFinder(model)
# Train a model with batch size 512 for 5 epochs
# with learning rate growing exponentially from 0.0001 to 1
lr_finder.find(x_train, y_train, start_lr=0.0001, end_lr=1, batch_size=512, epochs=5)# Plot the loss, ignore 20 batches in the beginning and 5 in the end
lr_finder.plot_loss(n_skip_beginning=20, n_skip_end=5)# Plot rate of change of the loss
# Ignore 20 batches in the beginning and 5 in the end
# Smooth the curve using simple moving average of 20 batches
# Limit the range for y axis to (-0.02, 0.01)
lr_finder.plot_loss_change(sma=20, n_skip_beginning=20, n_skip_end=5, y_lim=(-0.01, 0.01))Contributions are welcome. Please, file issues and submit pull requests on GitHub, or contact me directly.
This code is based on:
- The method described in section 3.3 of the 2015 paper "Cyclical Learning Rates for Training Neural Networks" by Leslie N. Smith
- The implementation of the algorithm in fastai library by Jeremy Howard. See fast.ai deep learning course for details.