-
- 找到最简单的子问题求解
- 终止条件
- 分解成哪几部分
- 其他问题不考虑内在细节,只考虑整体逻辑
- java题解思路
- 找到最简单的子问题求解
-
- 用两个指针镜像遍历, 判断是否相同
-
- 转化为求左右子树的深度和的最大值;
- 求子树深度的终止条件是 if (node == null) == > return 0;
- 所以递归方法的 deep(TreeNode node) 的返回值 = 左右子树中最大的深度 + 1(自身节点)
- 使用 deep(node) 的方式 遍历整棵树, 在此过程中, 使用一个变量 ans 更新记录每次遍历后的最长路径所需要的经过的节点个数; 每次遍历后 ans = max(ans, left_deep + right_deep + 1)
- 最后返回最长路径 = 最长路径经过的节点个数 - 1
-
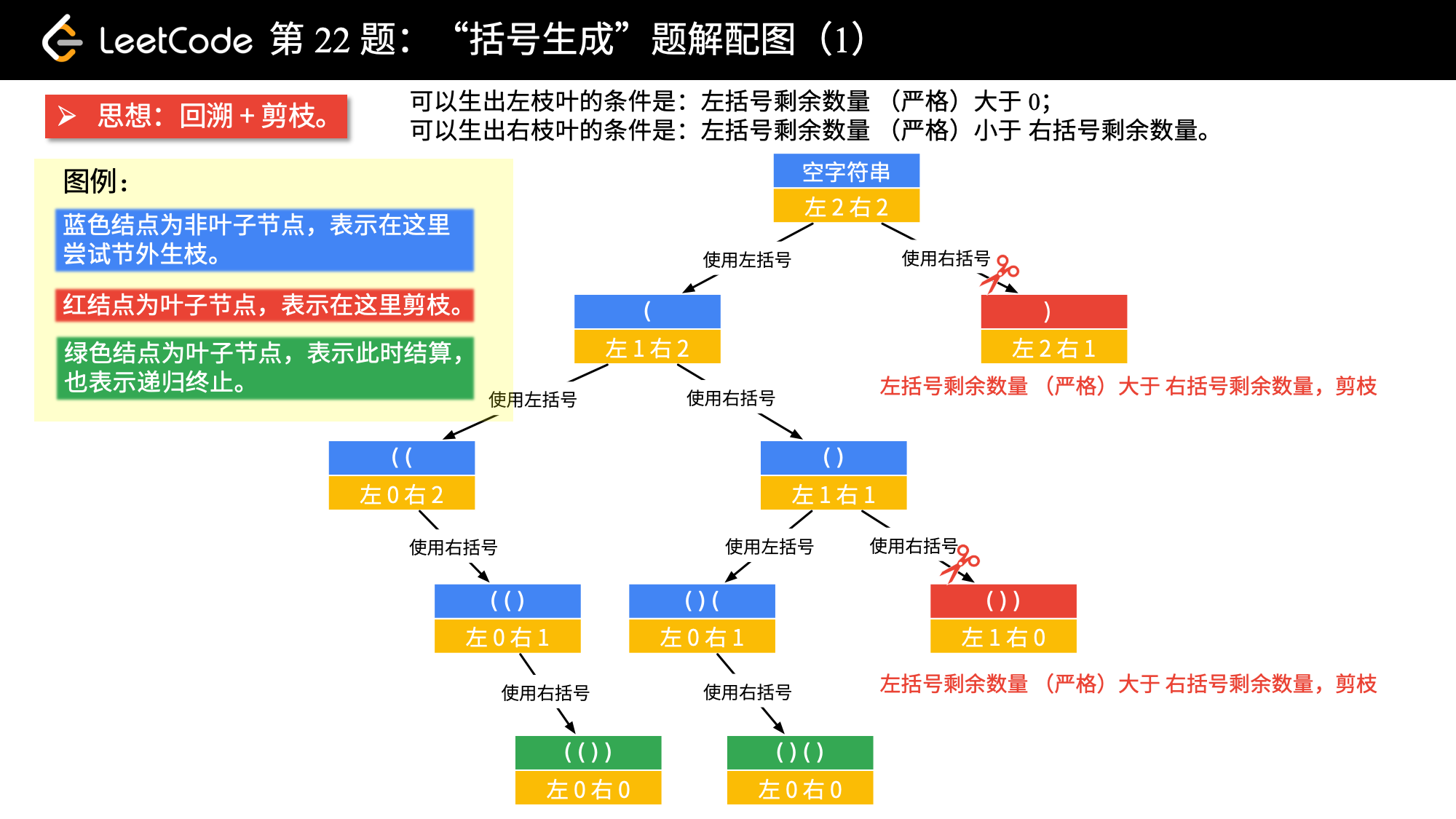
- 当前左右括号都有大于 00 个可以使用的时候,才产生分支;
- 产生左分支的时候,只看当前是否还有左括号可以使用;
- 产生右分支的时候,还受到左分支的限制,右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候,才可以产生分支;
- 在左边和右边剩余的括号数都等于 00 的时候结算。
-
实现一个 Trie (前缀树),包含
insert,search, 和startsWith这三个操作。
class TrieNode {
private boolean isEnd;
TrieNode[] next;
public TrieNode() {
this.isEnd = false;
this.next = new TrieNode[26];
}
}-
- 找到数学公式即可
-
- 递归
- 利用栈遍历
-
- 使用递归函数
dfs(root, p, q)返回root的子树是否含有 节点p或q - 当左右子树分别包含
p和q或 当前节点是p或q和其中一个子树包含另一个的时候 当前节点就是最近公共祖先
- 使用递归函数
-
- 用一个 map 来记录前缀和对应的出现的次数
- 使用查询 curSum-target 在 map 中的值来得到目标值在树中的路径的条数
-
-
利用深度优先递归的方法, 但是在递归中加入范围的控制
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public boolean isValidBST(TreeNode root) { return helper(root, null , null); } private boolean helper(TreeNode node, Integer lower, Integer upper) { // 注意, 此处的 lower 和 upper 的定义类型需要是 Integer, 凑则无法接收 null if (node == null) // 当节点为null 直接返回true return true; int value = node.val; if (lower != null && lower >= value) //超过左边界 return false; if (upper != null && upper <= value) // 超过右边界 return false; if (!helper(node.left, lower, value)) // 查看左子节点的有效情况 return false; if (!helper(node.right, value, upper)) // 查看右子节点的有效情况 return false; return true; } }
-
中序遍历
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public boolean isValidBST(TreeNode root) { if(root == null) return true; Deque<TreeNode> stack = new LinkedList<TreeNode>(); // 此处的变量用于保存之前的值, 便于在中序遍历的时候判断查找树能否保证后一个数大于前一个数, 由于测试例子中的最小数字可能是Integer.MIN_VALUE = -2147483648 , 在实现中不方便, 所以此处该变量的类型使用了double, 而Double.MIN_VALUE 的值是一个极小的正浮点数, 所以需要使用 -Double.MAX_VALUE double preNum = -Double.MAX_VALUE; while(!stack.isEmpty() || root != null) { // 栈不为空表示还有未处理的, root不为空表示整个树还没有遍历完成 while(root != null) { // 当root不为空的时候, 需要依次将左边的子节点加入到栈中 stack.push(root); root = root.left; } root = stack.pop(); // 到达了最左的位置 if (root.val <= preNum) // 判断是否符合中序遍历递增的条件 return false; preNum = root.val; // 记录新的递增判断值 root = root.right; // 由于当前root已然是最左, 需跳转到其右子节点进行遍历, 如果又子节点为null 则会从栈中提取出该节点的父节点进行判断 } return true; } }
-
-
- 利用搜索树的有序性质加速查找
-
-
自己想的方法是, 从左到右遍历找到逆序中的最小值 min , 并更新当前遇到的最大值,以此来找到右边界; 再从右边届向左遍历, 找出左边界.
-
看到两个比较巧妙的方法:
- 向右遍历, 用 left = nums.length-1 记录左边界; 记录当前的最大值max_previous; 当遇到cur_Num < max_previous 的时候, 就更新 left 的值 , 试着将所有比 cur_Num 大的数放到 左边界 left 右边去; 同时, 更新 right = cur_Num.index() . 这样 一次遍历就找出了左右边界.
class Solution { public int findUnsortedSubarray(int[] nums) { int len = nums.length; int max = nums[0]; int left = len; int right = 0; for (int i=1; i<len; i++) { if (nums[i] < max) { right = i; left = Math.min(i-1, left); while(left >= 0 && nums[left] > nums[i]) { // 此处直到 nums[left] <= nums[i] 就可以结束了, 所以判断总不需要加 '=' 符号 --left; } } else max = nums[i]; } // System.out.println(left); // System.out.println(right); return right > left ? right - left : 0; // 返回的结果中需要考虑到没有逆序的情况, 所以需要加一个判断 } }
-
使用一次for循环, 分别从两端相向而行来分别更新左右边界, 简洁而巧妙.
class Solution { public int findUnsortedSubarray(int[] nums) { int len = nums.length; int max = nums[0]; int min = nums[len-1]; int left = 0, right = -1; // 这样初始化的目的是, 当序列没有出现逆序的情况下, 结果正确, 为 0 for(int i=1; i<len; i++) { if (max > nums[i]) right = i; else max = nums[i]; if (min < nums[len-1-i]) left = len-1-i; else min = nums[len-1-i]; } return right - left + 1; } }
-
-
-
分别从左到右和从右到左两趟遍历来计算
class Solution { public int[] productExceptSelf(int[] nums) { int len = nums.length; int[] ans = new int[len]; ans[0] = 1; for(int i=1; i<len; i++) { // 从左到右依次计算得到每个点左边的乘积 ans[i] = ans[i-1] * nums[i-1]; } int right_multi = nums[len-1]; for(int i=len-2; i>=0; i--) { // 从右到左, 依次计算得到右边的乘积并整合 ans[i] *= right_multi; right_multi *= nums[i]; } return ans; } }
-
-
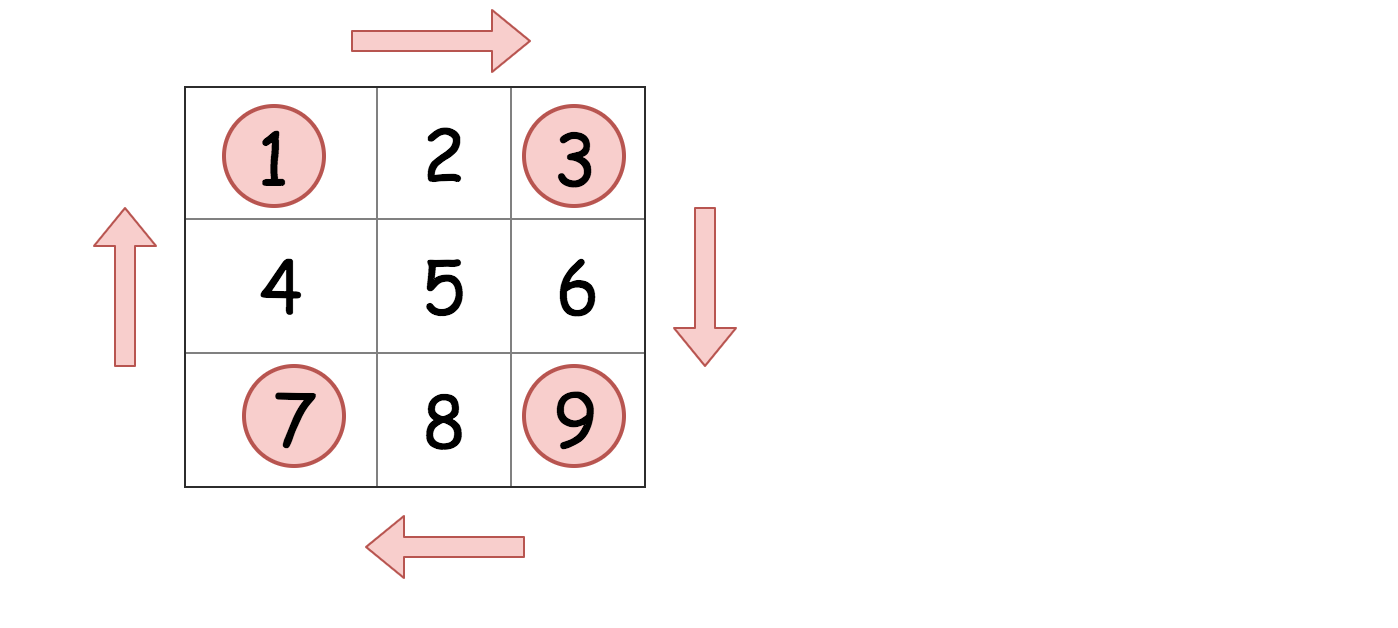
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
-
- 将二维dp用一维表示, 在另一个维度里再依次更新
-
- 先进行二维排序, 再依次按照第二个下标插入新的数组中
-
- 由于空间复杂度要求为O(1), 不能使用哈希表冲突判断法
- 可以使用二分法, 记录左右边界 left 和 right, 每次计算中间值mid, 和在mid左边的数字的数量cnt. 如果 cnt>mid , 表示重复的数字在cnt左半边, 否则重复的数字在cnt右半边. 当 left == right 的时候 表示找到了重复的数字.
-
- 使用字符串的每一位的ascii码的乘积来过滤字符串
- 使用前26个质数分别标识26个字母, 同分异构的单词乘积将是相同的, 不同分的单词乘积极大概率是不同的, 在此题中未出现冲突的现象. 有可能导致溢出, 目前未知是否会出现撞车
-
- 中间开花法(两种花: 1.有❤ 2.无❤)
-
基本方法:
class Solution: def topKFrequent(self, nums: List[int], k: int) -> List[int]: d = {} for i in nums: if i in d: d[i] += 1 else: d[i] = 1 d = sorted(d.items(), key=lambda item:item[1], reverse=True) return [i[0] for i in d[:k]]
couter方法:
class Solution: def topKFrequent(self, nums: List[int], k: int) -> List[int]: return [i[0] for i in Counter(nums).most_common(k)]
-
相同任务执行间隔需要有冷却时间n
-
-
python 先对左边界排序, 再依据条件依次添加到ans中
class Solution: def merge(self, intervals: List[List[int]]) -> List[List[int]]: newList = sorted(intervals, key=lambda x: x[0]) ans = [] for left, right in newList: if ans==[] or left > ans[-1][1]: # 新区域的左边界大于ans中最后一个区域的右边界, 则将其直接加入到ans中 ans.append([left, right]) else: ans[-1][1] = max(right, ans[-1][1]) # 否则, 需要比较新区域的右边界和ans中最后一个区域的右边界的大小来进行合并 return ans
-
java 实现
class Solution { public int[][] merge(int[][] intervals) { if(intervals.length == 0) return new int[0][2]; // 对二维数组进行排序 Arrays.sort(intervals, (list1, list2) -> list1[0] - list2[0]); List<int[]> rawAns = new ArrayList(); for(int[] pair:intervals) { int L = pair[0], R = pair[1]; // 将L, 和R 事先记录下来能够给后期的多次调用节省时间 if (rawAns.size() == 0 || rawAns.get(rawAns.size()-1)[1] < L) rawAns.add(new int[]{ L, R }); else rawAns.get(rawAns.size()-1)[1] = Math.max(rawAns.get(rawAns.size()-1)[1], R); } return rawAns.toArray(new int[rawAns.size()][2]); } }
-
-
-
暴力法
-
遍历矩阵中的每个元素,每次遇到 11,则将该元素作为正方形的左上角;
-
确定正方形的左上角后,根据左上角所在的行和列计算可能的最大正方形的边长(正方形的范围不能超出矩阵的行数和列数),在该边长范围内寻找只包含 11 的最大正方形;
-
每次在下方新增一行以及在右方新增一列,判断新增的行和列是否满足所有元素都是 11。
-
-
dp
-
我们用 dp(i, j) 表示以 dp(i, j) 为右下角,且只包含 1 的正方形的边长最大值。
-
如果该位置的值是 0,则 dp(i, j) = 0,因为当前位置不可能在由 1 组成的正方形中;
-
如果该位置的值是 1,则 **dp(i, j)**的值由其上方、左方和左上方的三个相邻位置的 dp值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下:
dp(i, j) = min( dp(i−1, j), dp(i−1, j−1), dp(i, j−1) ) + 1
-
-
dfs
-
随着深度遍历搜索的进行, 查找的方形的变长也逐次地提升 1
-
递归的过程加入了行控制, 从某一行开始往下搜索, 进行剪枝
-
如果以当前坐标为左上角的矩阵是合法的, 那么返回 当前的面积 和 从当前行递归开始查找边长+1的正方形的面积结果中最大的
/* 深度优先遍历 */ // 边长 二维输入矩阵 从矩阵的第几号开始找 public int dfs(int maLen, char[][] matrix, int k) { for (int i=k; i <= n-maLen; i++) { // 纵向从第 k 行到能容的下边长为maLen的正方形的行数开始查找 for (int j=0; j <= m-maLen; j++) { // 横向从第一列开始查找 if (judge(maLen, matrix, i, j)) // 如果以当前坐标为左上角的矩阵是合法的, 那么返回 当前的面积 和 从当前行递归开始查找边长+1的正方形的面积结果中最大的 return Math.max(maLen*maLen ,dfs(maLen+1, matrix, i)); } } return 0; }
-
-
-
-
有序二维数组查找的精髓就在于从右上角开始遍历, 若从左上开始的话则没有一个确定的方向, 向右和向下都是增加.
-
而从右上角开始遍历, 则有一个确定的遍历方向, 往左是变小, 往下是变大, 出了边界则是不存在, 十分巧妙
class Solution { public boolean searchMatrix(int[][] matrix, int target) { if (matrix.length == 0) return false; // 有序二维数组查找的精髓就在于从右上角开始遍历, 若从左上开始的话则没有一个确定的方向, 向右和向下都是增加. // 而从右上角开始遍历, 则有一个确定的遍历方向, 往左是变小, 往下是变大, 出了边界则是不存在, 十分巧妙 int col = matrix[0].length - 1; int row = 0; while(col>= 0 && row < matrix.length) { if(matrix[row][col] == target) { return true; } if(matrix[row][col] < target) row++; else col--; } return false; } }
-
-
-
利用贪心思想, 在从左到右的查找过程中维护一个最远可达距离
class Solution: def canJump(self, nums: List[int]) -> bool: if not nums: return False if nums[0] == 0 and len(nums) > 1: return False if len(nums) == 1: return True farthest = 0 n = len(nums) for i in range(n): if i <= farthest: farthest = max(farthest, i+nums[i]) if farthest >= n-1: return True else: return False return False
-
-
-
普通法
-
二分查找(适用于大型的数组)
class Solution { public int[] searchRange(int[] nums, int target) { int[] ans = {-1, -1}; if (nums == null || nums.length == 0) return ans; int leftIndex = getLeftOrRight(nums, target, true); if ( leftIndex == nums.length || nums[leftIndex] != target ) // 要先判断出错的情况, 再判断没有找到的情况 ( 首先保证程序的正常运行! 否则直接调用这个下标会产生下标溢出的错误 ) return ans; ans[0] = leftIndex; ans[1] = getLeftOrRight(nums, target, false); return ans; } private int getLeftOrRight(int[] nums, int target, boolean Left) { int low = 0; int high = nums.length; while(low < high) { int mid = (low + high) / 2; if (nums[mid] > target || Left && nums[mid] == target) high = mid; else low = mid + 1; } return Left ? low : low - 1 ; // 当找右边界的时候 需要 - 1 } }
-
-
-
带有双层判断的二分查找, 先找有序的部分, 再判断其中是否包含要查找的元素, 若包含则在该部分查找, 否则去另一边查找
class Solution { public int search(int[] nums, int target) { int lo = 0, hi = nums.length-1; while(lo <= hi) { int mid = (lo + hi) / 2; if (nums[mid] == target) // 当找到时, 直接返回其位置 return mid; if (nums[lo] <= nums[mid]) { // 若左边有序 if (nums[lo] <= target && target < nums[mid]) // 判断其中是否包含target hi = mid - 1; // 包含则在其中找 else lo = mid + 1; // 不包含则到右边去找 } else { // 左边无序 if (nums[mid] < target && target <= nums[hi]) // 判断右边有序的部分是否包含target lo = mid + 1; // 右边有序部分包含target则在右边找 else hi = mid - 1; // 右边不包含则回到左边去找 } } return -1; } }
-
-
-
先从右到左找到上升点的左边位置 i , 然后再从右往左找比这个值稍大一点的值的位置 j , 交换两个值, 然后翻转 i 右边的元素
class Solution { public void nextPermutation(int[] nums) { int len = nums.length;; int i = len - 2; while(i>=0 && nums[i] >= nums[i+1]) i--; if (i>=0){ // 若当前数已经是最大值了, i = -1 int j = len -1; while(j>i && nums[i] >= nums[j]) // 找到能使得 nums[j] > nums[i] 的 j j--; swap(nums, i, j); // 交换两个值 } reverse(nums, i+1); // 无论如何, 翻转下标 i 之后的子数组 } // 翻转函数 private void reverse(int[] nums, int start) { int end = nums.length-1; while(start < end) { swap(nums, start, end); start++; end--; } } // 交换两个值的函数 private void swap(int[] nums, int i, int j) { int tmp = nums[i]; nums[i] = nums[j]; nums[j] = tmp; } }
-
-
- 利用字符数组加快迭代, 将最长子串的下标设置为类的私有变量, 在迭代中更新下标 start 和 end , 同时在每轮迭代的过程先移动end到与start不相同的首位置, 且将idx更新到该位置, 便于下一次的快速迭代 ```java class Solution { int start; int end; public String longestPalindrome(String s) { char c[] = s.toCharArray(); // 使用字符数组查找更加快捷 start = end = 0; // 初始化开始和结束点 calLongest(c, 0); // 迭代 return s.substring(start, end); } private void calLongest(char[] c, int idx) { if (idx > c.length-1) return; // 超出范围终止迭代 int start_ = idx, end_ = idx; while(end_+1 < c.length && c[end_+1] == c[end_]) ++end_; idx = end_; // 该步骤优化了8ms, 将 idx 移到 重复元素的末尾 end_ 处, 避免重复迭代 while(start_>=0 && end_<c.length && c[start_]==c[end_]) { start_--; end_++; } if(end_ - start_ -1 > end - start) { start = start_+1; end = end_; } calLongest(c, idx+1); } } ``` -
法一: 从左到右和从右到左分别记录当前最大值, 形成两个列表, 其中重叠部分, 也就是两个列表对应位置的最小值就是地面加上雨水的高度, 再减去地面的高度便得到了雨水的量
class Solution { public int trap(int[] height) { if (height == null || height.length == 0) return 0; int ans = 0; int size = height.length; int[] left_max = new int[size]; int[] right_max = new int[size]; left_max[0] = height[0]; for (int i = 1; i < size; i++) { left_max[i] = Math.max(height[i], left_max[i - 1]); } right_max[size - 1] = height[size - 1]; for (int i = size - 2; i >= 0; i--) { right_max[i] = Math.max(height[i], right_max[i + 1]); } for (int i = 1; i < size - 1; i++) { ans += Math.min(left_max[i], right_max[i]) - height[i]; // 重叠部分减去底就是装的水的量 } return ans; } }
法二: 使用双指针的方法, 左右指针分别向中间依次移动, 每当遇到小于等于当前高度的就一直往中间移动, 而当遇到更高的, 则移动过去, 但让另一个指针开始移动
public int trap(int[] height) { int left = 0, right = height.length - 1; int ans = 0; int left_max = 0, right_max = 0; while (left < right) { if (height[left] < height[right]) { if (height[left] >= left_max) { left_max = height[left]; } else { ans += (left_max - height[left]); } ++left; } else { if (height[right] >= right_max) { right_max = height[right]; } else { ans += (right_max - height[right]); } --right; } } return ans; }
- 法一: 利用map来记录数组中的元素, 当该数可能为连续数字的开头的时候开始计算最长的连续长度, 并维护最大值
- 法二: 计算最大和最小的数, 从而建立索引数组, 再计算连续的最长长度是多少
-
- 使用快慢指针, 快的步长为2, 慢的步长为1. 如果存在环则快慢指针定会相遇; 否则快指针会先到达链尾
-
- 法1: 快慢指针+栈, 在慢指针到达中间的时候开始判断是否回文
- 法2: 利用快慢指针快速找到中间节点的同时, 将前半部分的链表指针翻转, 再从中间向两端遍历判断是否相同以构成回文. 最后将链表指针顺序恢复. (空间利用率更低, 速度更快)
-
-
递归方法: 先处理后边的, 再处理当前的
class Solution { private ListNode res; private ListNode temp; public ListNode reverseList(ListNode head) { if(head==null || head.next==null) return head; ListNode ptr = head; dfs(ptr); return res; } private void dfs(ListNode ptr) { if(ptr.next != null ){ dfs(ptr.next); temp.next = new ListNode(ptr.val); temp = temp.next; } else{ res = new ListNode(ptr.val); temp = res; } } } -
遍历方法: 头插法
class Solution { public ListNode reverseList(ListNode head) { if(head == null) return head; ListNode ans = null; while(head != null){ ListNode h = head.next; head.next = ans; ans = head; head = h; } return ans; } }
-
-
-
示例:
输入: 2->1->3->5->6->4->7->NULL 输出: 2->3->6->7->1->5->4->NULL
-
用两个指针交替拆线将原链表分成两个分别保存奇偶序号节点的链表, 最终完成拼接
class Solution { public ListNode oddEvenList(ListNode head) { if(head == null || head.next == null) return head; ListNode odd_tail = head; ListNode even_head = head.next; ListNode even_tail = even_head; ListNode t; while(even_tail != null && even_tail.next != null) { odd_tail.next = even_tail.next; odd_tail = odd_tail.next; even_tail.next = odd_tail.next; even_tail = even_tail.next; } odd_tail.next = even_head; return head; } } 最终会出现两种情况: 1) odd_tail -> even_tail(null) 2) odd_tail -> even_tail -> null 在 odd_tail.next = even_head; 后都能完成拼接操作.
-
-
- 归并(用快慢指针找中心点)
- 快排序(分为less和more两个子链表, 递归求解)
-
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
- 使用双指针
- 快指针若检测到null, 说明没有环, 返回null
- 若出现fast == slow, 则有环
- 用 f 表示快指针走的路程, s 表示慢指针走的路程
- f = 2s (快指针走的路程是慢指针的2倍)
- f = s + nb (快指针比慢指针多走了 n 个环的距离 )
- 从上式得到: f = 2nb, s = nb; 即 快慢指针分别走了2n , n 个环的周长。(n是未知数)
- 分析: 从链表头能走到环的入口的步数是 k = a + nb 。 a 是从头到环入口的距离。
- 此时只需要让s 再走a 步便能到达环的入口。
- 想到让快指针重新指向head,让其与s同步前行,直到两指针相遇, 则说明正好走了a步,而此时快慢指针指向的都是环的入口。
-
-
双指针, 先让两个指针相隔n, 当后面的指针为null 的之后, 删除前面的指针的后面一个元素(注意: 需要利用辅助头结点)
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * } */ class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummyHead = new ListNode(0, head); // 在前面建立一个辅助头节点 ListNode left = dummyHead, right = dummyHead; // 初始化两个指针 while (n-- != -1) { // 让右指针向后移动 n + 1 步 right = right.next; } while (right != null) { // 当右指针 left = left.next; right = right.next; } left.next = left.next.next; return dummyHead.next; } }
-
-
-
依次合并到一个新的链表, 需要一个伪头结点
-
需要一个进位变量
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ class Solution { public ListNode addTwoNumbers(ListNode l1, ListNode l2) { ListNode DummyHead = new ListNode(0); ListNode cur = DummyHead; int Carry = 0; while( l1 != null || l2 != null || Carry > 0) { int sum = ((l1 != null) ? l1.val : 0) + ((l2 != null) ? l2.val : 0) + Carry; Carry = sum / 10; cur.next = new ListNode(sum % 10); cur = cur.next; if(l1 != null) l1 = l1.next; if(l2 != null) l2 = l2.next; } return DummyHead.next; } }
-
-
-
使用二分分治来合并
class Solution { //主函数 public ListNode mergeKLists(ListNode[] lists) { return merge(lists, 0, lists.length - 1); } // 使用二分分治来合并 public ListNode merge(ListNode[] lists, int l, int r) { if (l == r) { return lists[l]; } if (l > r) { return null; } int mid = (l + r) >> 1; return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r)); } // 合并两个链表 public ListNode mergeTwoLists(ListNode a, ListNode b) { if (a == null || b == null) { return a != null ? a : b; } ListNode head = new ListNode(0); ListNode tail = head, aPtr = a, bPtr = b; while (aPtr != null && bPtr != null) { if (aPtr.val < bPtr.val) { tail.next = aPtr; aPtr = aPtr.next; } else { tail.next = bPtr; bPtr = bPtr.next; } tail = tail.next; } tail.next = (aPtr != null ? aPtr : bPtr); return head.next; } }
-
-
- dfs方法通过
-
- 二分法的状态判断
-
for c in string: # 遍历字符串 if c is 左括号: stack.push(c) # 如果是左括号就入栈 else: if stack.isEmpty(): # 若是右括号且栈为空, 即栈中没有能与之匹配的左括号 return False if 左右括号匹配: stack.pop() # 左右括号匹配, 将栈中左括号弹出 else: return False # 栈虽不为空, 但是栈顶左括号与当前右括号不匹配, 不合法 return stack.isEmpty() # 仅当遍历结束后栈为空时, 字符串合法
-
-
利用栈的思想, 解决其嵌套问题
class Solution { int ptr; public String decodeString(String s) { ptr = 0; LinkedList<String> stk = new LinkedList<String>(); while(ptr < s.length()) { char cur = s.charAt(ptr); if (Character.isDigit(cur)) { // 是数字, 则找出该指针位置开始的连续数字的子串 String digits = getDigits(s); stk.addLast(digits); //入栈 } else if (Character.isLetter(cur) || cur == '[') { // 字母或者 '[' stk.addLast(String.valueOf(cur)); // 入栈 ptr++; } else { // 右括号 ptr++; LinkedList<String> sub = new LinkedList<String>(); //用来存放需要重复的字母的列表 while (!"[".equals(stk.peekLast())) { sub.addLast(stk.removeLast()); // 获取逆向字母 } stk.removeLast(); // 左括号出栈 Collections.reverse(sub); // 翻转成正向字母列表 int repNum = Integer.parseInt(stk.removeLast()); // 获取重复次数 StringBuilder sb = new StringBuilder(); String subStr = getString(sub); // 获取子串字符串 while(repNum-- >0) // 根据重复次数重复 sb.append(subStr); stk.addLast(sb.toString()); // 添加到栈中 } } return getString(stk); } // 获取s字符串中当前指针位置开始的一个数字子字符串 private String getDigits(String s) { StringBuilder sb = new StringBuilder(); sb.append(s.charAt(ptr++)); while(Character.isDigit(s.charAt(ptr))) { sb.append(s.charAt(ptr++)); } return sb.toString(); } // 从列表中获取拼接后的字符串 private String getString(List<String> strList) { StringBuilder sb = new StringBuilder(); for(String str:strList) { sb.append(str); } return sb.toString(); } }
-
-
- 利用栈的属性来找到以每个点的高度作为矩形的高的边界
-
- 开始操作前确定队列中的该层节点个数, 依次将上层元素放入新数组中并出队列, 将下层元素依次入队列
class Solution { public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> ans = new ArrayList(); if(root == null) { return ans; } else{ Queue queue = new LinkedList<TreeNode>(); queue.add(root); while(!queue.isEmpty()){ List<Integer> newList = new ArrayList(); int levelSize = queue.size(); for(int i=0; i<levelSize; i++) { TreeNode curNode = (TreeNode)queue.poll(); newList.add(curNode.val); if(curNode.left != null) queue.add(curNode.left); if(curNode.right != null) queue.add(curNode.right); } ans.add(newList); } return ans; } } }
-
- 每次遍历的时候, 更新当前 sum 的最大值: if cur<=0 ==> sum; else sum += cur;
- ans = max(ans, sum) : 在每次遍历后使用 max() 方法 更新最优解
分治思想:
将纠结空间分成左半部分, 右半部分, 和包含中间 mid, mid+1的部分这3 块来求解.
最后取这三部分中的最大值为最终的结果, 使用递归的方式来实现.
-
- 斐波那契数列, 使用递归或者滚动数组的思想
-
- 用变量 Sn保存抢前n家所能获得的最大的金额, 用 Mn表示第n家的金额
- Sn = max (Sn-2 + Mn , Sn-1)
- 为了减少空间利用率, 可以用滚动数组的方式.
-
class Solution { public int[] dailyTemperatures(int[] T){ int n = T.length; int[] res = new int[n]; for(int i = n - 1; i >= 0; i--){ // 从后往前遍历 int j = i + 1; // 从天的后一天开始查找 while(j < n){ if(T[j] > T[i]){ // 如果遇到更高的温度,便记录其时间跨度 res[i] = j - i; break; }else if(res[j] == 0){ // 表示明天温度不比当天高,且明天之后没有更高的温度, 则保持 0 break; }else { j += res[j]; // 跳转到从第 j 天跳转到首次温度比它高的那一天 } } } return res; } }
-
class Solution { public int uniquePaths(int m, int n) { int[][] T = new int[m][n]; // 用于记录已经计算过的情况 return calcu(--m, --n, T); // 此处需要将 m, n 减1 , 因为机器人初试位置已经在横纵都占了一格了 } private int calcu(int m, int n, int[][] T) { if(m>0 && n>0){ // 当前点非边缘的时候, 计算方式是两种走法的路径数量和 if(T[m][n] == 0) { // 如果没有计算过, 就计算 int tmp = calcu(m-1, n, T) + calcu(m, n-1, T); T[m][n] = tmp; // 并记录下来 return tmp; }else return T[m][n]; // 如果已经计算过就直接返回 } else{ return 1; // 如果是边缘, 就返回 1 , 因为只有一条路径 } } }
-
-
每个节点有两种情况, 则有两个不同的输出, 所以想到用数组来表示结果
class Solution { public int rob(TreeNode root) { int[] result = robinterval(root); return Math.max(result[0], result[1]); } public int[] robinterval(TreeNode root) { if(root == null) return new int[2]; int result[] = new int[2]; // 下标为0 记录当前节点不抢, 下标为1记录当前节点抢 int[] left = robinterval(root.left); int[] right = robinterval(root.right); //当不选当前节点的时候, 从两个子节点中分别选出最大的(子节点抢或不抢) result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]); //当选择当前节点的时候, 两个子节点不能抢 result[1] = root.val + left[0] + right[0]; return result; } }
-
-
-
先设置为最大值, 然后通过dp来更新优化
class Solution { public int numSquares(int n) { int[] dp = new int[n+1]; for(int i=1; i<n+1; i++) { dp[i] = i; } for(int i=1; i<n+1; i++) { for(int j=1; i-j*j >= 0; j++) { dp[i] = Math.min(dp[i], dp[i-j*j] + 1); } } return dp[n]; } }
-
-
-
将事件分为不同的状态,根据不同的状态之间的关系来写出他们之间的转换方程,这是算法的核心部分
-
在程序设计的时候,动态规划的表达式如dp[i][0] 一般表示第i天结束后的状态为0,记录当天操作后的状态会比较好。
class Solution { public int maxProfit(int[] prices) { int n = prices.length; if(n == 0) { return 0; } int[][] dp = new int[n][3]; dp[0][1] = -prices[0]; for(int i=1; i<n; i++) { dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2]); // 可以购买股票 dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]); // 可以卖出股票 dp[i][2] = dp[i-1][1] + prices[i]; // 在冷冻期 } return Math.max(dp[n-1][0], dp[n-1][2]); } }
-
-
-
使用一个 target + 1 大小的数组来记录是否能用数字拼接成该下标的值
-
更新该数组, 直到找到 能使得 该数组中 target 为 true 的情况存在, 返回 true; 找不到则返回 false
class Solution { public boolean canPartition(int[] nums) { int len = nums.length; // 获取nums 长度 if (len == 0) return false; int sum = Arrays.stream(nums).sum(); // 获取数组的和 if((sum & 1) == 1) // 如果和是奇数则直接返回false return false; int target = sum / 2; // 获取到平分后的目标值, 也就是每一份应该达到的值, 在找的时候只要找到该值就可以判定是否能平分数组了 boolean[] ok = new boolean[target + 1]; // 该数组用于记录某下标能否由某些数字之和形成 ok[0] = true; // 初始化, 0 是肯定能达成的, 而且对于后续的循环迭代有很重要的作用. for(int i=0; i<len; i++) { for(int j=target; j>=0; j--) { if(ok[j]&&j+nums[i]<=target){ // 每当j是可以形成的, 且 j + nums中的某个数是小于等于目标值target的时候, 就在ok数组中更新该 j + nums[i] 对应的值为true, 表示可以形成该值. ok[j+nums[i]] = true; if(j+nums[i] == target) // 而当j + nums[i] 正好等于 target 的时候, 说明找到了某种能平分的解决办法 return true; } } } return false; } }
-
-
-
用数组记录到某一位置下标的子串是否满足条件, 从而进行递进的判断
class Solution: def wordBreak(self, s: str, wordDict: List[str]) -> bool: n = len(s) dp = [False]*(n+1) dp[0] = True for i in range(n): for j in range(i+1, n+1): if dp[i] and s[i:j] in wordDict: # 如果i以前都是合法的, 那么遍历从i到j(左闭右开) 判断是否有满足字典中的单词的字符串, 如果有的话就将该dp值置为 True dp[j] = True return dp[-1];
-
-
- 法一: 利用动态规划, dp[i] 表示以下标 i 为末尾元素的子串的最大上升子序列的长度
- 法二:
- 利用贪心的思想, 如果希望上升子序列最长, 则需要让子序列的上升坡度尽可能的缓
- 维护一个数组 d[] , 数组的长度 len 表示当前最长子序列的长度, 数组的最后一个元素表示, 当前最长上升子序列的最大元素.
- 遍历原始序列
- 若当前元素nums[i] > d[len] , 则 nums[++len] = nums[i]
- 否则在 d 中利用二分查找法找到第一个大于 nums[i] 的元素 K, 并用 nums[i] 替代 K.
-
-
法1: 深度优先
-
法2: 二维数组动态规划
-
法3: 公式法简化问题, 利用一位数组动态规划
class Solution { /* nums 中的所有的元素的和记为 sum, 假设nums中存在某一种元素的组合方式 w = x1+x2+...+xk , 使得 sum - 2w = S, 所以 w = (sum - S) / 2 。此时已经获得了 w 的确切值, 但是不知道组成 w 的方式有多少种, 所以想到可以使用动态规划的方式来进行解答, dp[i] 记录 和为 i 的组成方式的个数. */ public int findTargetSumWays(int[] nums, int S) { int sum = 0; for (int num : nums) { sum += num; } if (sum < S || (sum + S) % 2 == 1) { return 0; } int w = (sum - S) / 2; int[] dp = new int[w+1]; dp[0] = 1; for(int num:nums) { // 获取每个迭代的跨度 for(int j=w; j>=num; j--) { // 从所有元素和往下知道到达当前跨度依次尝试有无基于原来和的累加的可能性 dp[j] += dp[j-num]; } } return dp[w]; } }
-
-
-
线性数组 dp
public class Solution { public int coinChange(int[] coins, int amount) { int[] dp = new int[amount+1]; // dp记录和为下标的组合个数 Arrays.fill(dp, amount+1); // 初始化为最大值 dp[0] = 0; // 和为0的个数是0 for(int i=1; i<=amount; i++) { // i 遍历所有可能的和的值 for(int j=0; j<coins.length; j++) { // 遍历所有币的面值 if(coins[j] <= i) // 当面值小于等于和的时候 dp[i] = Math.min(dp[i], dp[i-coins[j]] + 1); // 更新dp值为当前值和去掉当前面值的可能个数+1 } } return dp[amount] > amount ? -1:dp[amount]; } }
-
-
-
由于负数的存在, 需要保存最大和最小值两个变量, 并依据当前值来更新
class Solution { public int maxProduct(int[] nums) { int max = Integer.MIN_VALUE, imax = 1, imin = 1; for(int num:nums) { if(num<0){ // 出现负数, 交换最大和最小 int tmp = imax; imax = imin; imin = tmp; } // 最大值与当前值相乘, 和当前值进行比较, 取最大的为迭代中的最大值 // 最小值同理 imax = Math.max(imax * num, num); // 更新最大值 imin = Math.min(imin * num, num); // 更新最小值 max = Math.max(max, imax); // 用全局变量max 来记录迭代过程中出现的最大值 } return max; } }
-
-
-
dp[i][j]表示戳k方案中的最优解, 其中 i<k<j
class Solution { public int maxCoins(int[] nums) { //避免空指针异常 if (nums == null) { return 0; } //创建虚拟边界 int length = nums.length; int[] nums2 = new int[length + 2]; System.arraycopy(nums, 0, nums2, 1, length); nums2[0] = 1; nums2[length + 1] = 1; length = nums2.length; //创建dp表 length = nums2.length; int[][] dp = new int[length][length]; // dp[i][j]表示戳k方案中的最优解, 其中 i<k<j //开始dp:i为begin,j为end,k为在i、j区间划分子问题时的边界 for (int i = length - 2; i > -1; i--) { for (int j = i + 2; j < length; j++) { //维护一个最大值;如果i、j相邻,值为0 int max = 0; for (int k = i + 1; k < j; k++) { int temp = dp[i][k] + dp[k][j] + nums2[i] * nums2[k] * nums2[j]; // if (temp > max) { max = temp; } } dp[i][j] = max; // 找到戳 i 和 j 中间(不包括i和j)的最大方案 } } return dp[0][length-1]; } }
-
-
- 化解为一维数组的柱状图的最大面积问题
-
遍历思想
//python3 class Solution: def subsets(self, nums: List[int]) -> List[List[int]]: res = [[]] for num in nums: res += [[num] + arr for arr in res] return res; ----------------------------------------------------------------- //java class Solution { public List> subsets(int[] nums) { List> res = new ArrayList(); res.add(new ArrayList()); for (int num:nums){ List> tempArr = new ArrayList(); for (List subArr:res){ tempArr.add(new ArrayList(subArr){{add(num);}}); } for (List arr:tempArr) res.add(arr); } return res; } }递归思想
class Solution: def subsets(self, nums: List[int]) -> List[List[int]]: res = [] n = len(nums) def helper(i, temp): res.append(temp) for j in range(i, n): helper(j+1, temp + [nums[j]]) helper(0, []) return res;回溯思想
class Solution { public List> subsets(int[] nums) { List> res = new ArrayList(); backtrack(0, nums, res, new ArrayList()); return res; } public void backtrack(int i, int[] nums, List> res, ArrayList temp) { res.add(new ArrayList(temp)); for (int j=i; j<>nums.length; j++) { temp.add(nums[j]); backtrack(j+1, nums, res, temp); temp.remove(temp.size()-1); } } } -
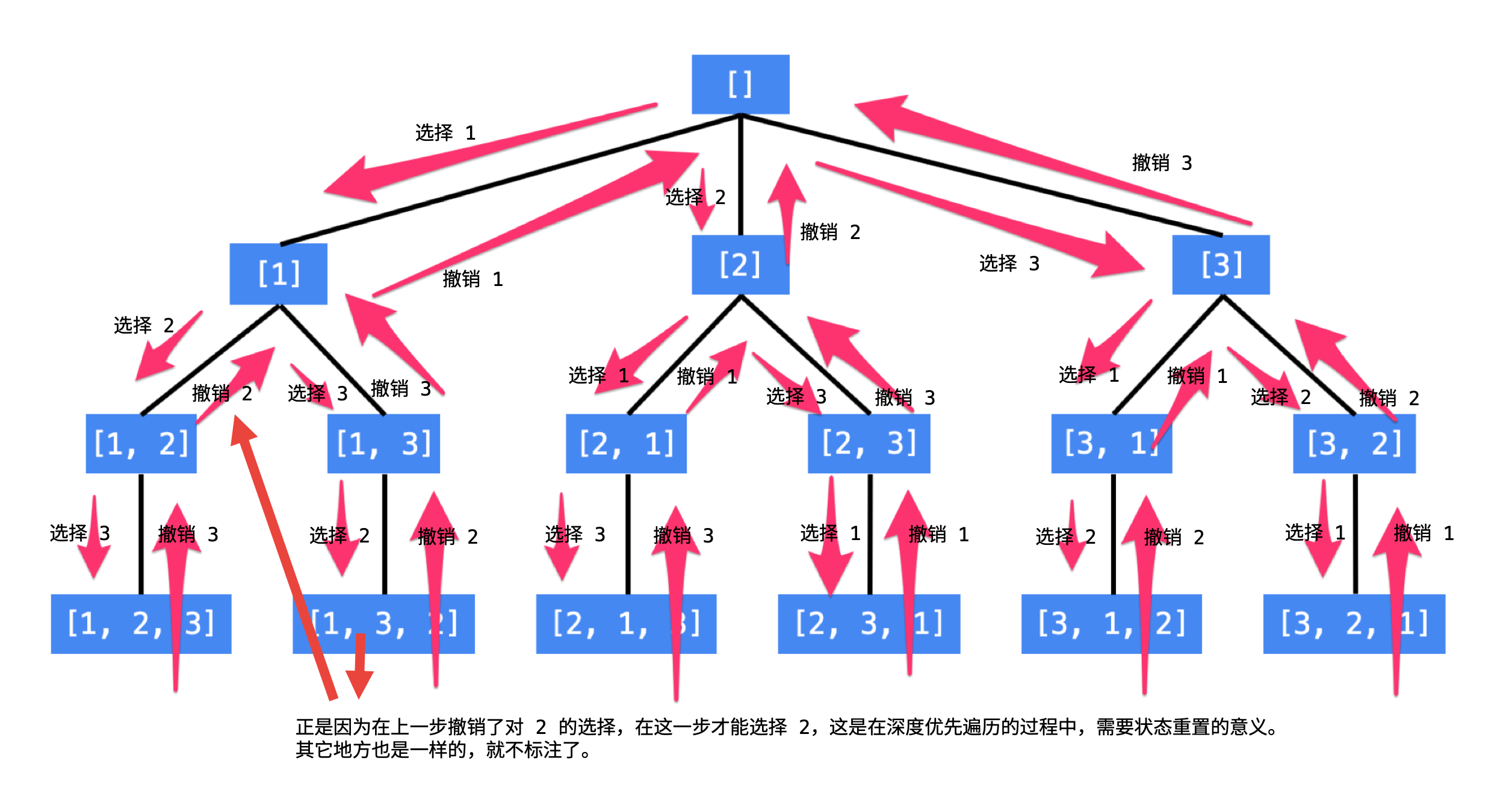
- 利用树形结构 + 回溯
- 使用 path 记录深度优先遍历的路径, used[] 记录节点是否在path中
- 终止条件: 当path长度等于数组长度的时候, 将 path添加到 res 数组中
- 在此过程中如果节点不在path中, 就将其加入并设置uesd 为true, 然后dfs递归. 在递归结束后恢复递归前的状态, 即将最新加入的节点删除并置used为false, 此即回溯的含义.
for(int i=0; i<nums.length; i++) { if(!used[i]){ used[i] = true; path.add(nums[i]); dfs(used, nums, res, path, depth+1); used[i] = false; path.remove(path.size()-1); } }
-
- 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
- 遍历candidates, 记录path, 记录当前遍历的index, 在未满足条件的情况下使用当前index作为起始点继续寻找, 使得该点能够被重复添加到path中; 在寻找的过程中, 没加入一个点, 就在target中减去这个值, 当target == 0 的时候, 就将path中的点组成的list加入到res中.
- 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
-
- 本题的实质上可以概括为这样一个模型
- 存在一种一对多的映射 A -> B
- 指定A 中元素的一种排列, 需要得出 A中元素所对应的 所有可能的 B 中元素的排列
- 这种全排列问题可以使用回溯法进行一一枚举
class Solution { public List<String> letterCombinations(String digits) { List<String> combinations = new ArrayList<String>(); // 用来暂存当前的字符列表(会在回溯查找的过程中不断地变化) if(digits.length() == 0) { return combinations; } Map<Character, String> phoneMap = new HashMap<Character, String>() {{ // 添加map映射 put('2', "abc"); put('3', "def"); put('4', "ghi"); put('5', "jkl"); put('6', "mno"); put('7', "pqrs"); put('8', "tuv"); put('9', "wxyz"); }}; backtrack(combinations, phoneMap, digits, 0, new StringBuilder()); // 开始查找 return combinations; } public void backtrack(List<String> combinations, Map<Character, String> phoneMap, String digits, int index, StringBuilder combination) { if(index == digits.length()) // 当下标等于输入数字字符的长度的时候, 说明一种结果已经产生, 将其加入到结果列表中 combinations.add(combination.toString()); else{ // 否则, 继续进行回溯查找 char digit = digits.charAt(index); // index 表示当前combinations中字符串的长度. 使用该长度作为下标索引找出digits中需要新添加的字母所对应的数字. String letters = phoneMap.get(digit); // 通过该数字, 在map中找到对应的所有字母字符组成的字符串 var lettersCount = letters.length(); // 获取到数字对应的字符的个数, 即字符串的长度 for(int i=0; i<lettersCount; i++) { // 回溯历该字符串中的所有元素, 分别将其加入到暂存字符列表combinations中, 加入后递归进行查找,交给下一层. 在下一层处理完毕退出函数之后, 表示该种可能已经全部考虑完毕,则需要还原查找状态, 删除掉暂存字符列表中的最后一个元素, 便于下一次查找. combination.append(letters.charAt(i)); backtrack(combinations, phoneMap, digits, index + 1, combination); combination.deleteCharAt(index); } } } }
- 本题的实质上可以概括为这样一个模型
-
-
网格搜索阵列 + 变量私有化 + 访问控制形式的无线性轨迹反馈
class Solution { private int m, n; // 网格的行数 m , 和列数 n private int[][] direction = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}}; // 四个方向的偏移参数二维列表(常常用在网格搜索当中) private char[][] board; private String word; private boolean[][] visited; // 标记是否已经被访问过 public boolean exist(char[][] board, String word) { this.board = board; this.word = word; m = board.length; if(m == 0) return false; n = board[0].length; this.visited = new boolean[m][n]; // 依次从网格中的每个点作为开头来找 for(int i=0; i<m; i++) { for(int j=0; j<n; j++) { if(search(i, j, 0)) // 当搜寻结果为真的时候, 直接返回真 return true; } } return false; //没有找到, 返回假 } // 回溯搜索函数 private boolean search(int x, int y, int idx) { if (idx == word.length()-1) { // 当访问到单词的最后一个元素的时候, 直接判断是否相同, 来返回结果 return board[x][y] == word.charAt(idx); } if(board[x][y] == word.charAt(idx)) { // 不是最后一个单词, 则需要继续往后查找 visited[x][y] = true; // 访问标记 for(int k=0; k<4; k++) { int newX = x + direction[k][0]; int newY = y + direction[k][1]; if(inArea(newX, newY) && !visited[newX][newY]) { // 查找的条件是没有超出边界且没有访问过 if(search(newX, newY, idx+1)) return true; } } visited[x][y] = false; //去除访问标记, 便于回溯 } return false; } //区域合法性检测 private boolean inArea(int x, int y) { return x>=0 && x<m && y>=0 && y<n; } }
-
-
- 一个数乘以2后其就是左移一位, 1 的个数不会改变, 一个偶数a, a+1 的 1 的个数是 res[a] + 1
展开 java 递归代码
class Solution { private int[] res; public int[] countBits(int num) { res = new int[num + 1]; if (num == 0) { return res; } res[1] = 1; helper(num, 1, 1); return res; } private void helper(int num, int i, int count) { i = i << 1; // i *= 2 if (i <= num) { res[i] = count; // 左移1的个数不改变 helper(num, i, count); } i += 1; // 此时 i 必定为奇数 if (i <= num) { res[i] = count + 1; 此奇数的1的个数必定是前一个偶数的1的个数+1 helper(num, i, count + 1); } } } -
- 使用递归
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList();
dfs(res, root);
return res;
}
private void dfs(List<Integer> res, TreeNode node) {
if(node == null)
return;
dfs(res, node.left);
res.add(node.val);
dfs(res, node.right);
}
}-
-
在递归中进行变换: 从最底层开始变换(先递归再变换)
public void flatten(TreeNode root) { if(root == null) return; /*这两句可以调换顺序, 不影响结果, 区别是默认优先从左子树还是右字数进行变换*/ flatten(root.left); // (1) flatten(root.right); // (2) // 暂存右子树, 左边移到右边, 左边置为空 TreeNode temp = root.right; root.right = root.left; root.left = null; // 移到当前右子树的最右下端, 将旧的右子树接到其下 while(root.right != null) root = root.right; root.right = temp; }
-
-
- 在大循环中当遇到没有被访问的点就将大陆数量 + 1, 然后进行深度搜索
- 利用深度优先搜索依次对上下左右的临界区域进行判断, 如果仍然是大陆则对其进行同化标记并递归搜索.
-
- 使用递归方法, 计算每个节点为根所能达到的最大值, 在递归中更新ans
-
- 可以利用斐波那契数列和3个变量来循环求解
-
- 使用快速排序的思想, 对第k个元素存在的一半进行进一步的递归划分排序
-
class Solution { public int maxArea(int[] height) { int ans = 0; int left = 0; int right = height.length-1; while(left < right){ if(height[left] > height[right]){ // 取右边的高度为高 int cap_height = height[right]; int cap = (right - left) * cap_height; // 计算容积 if(cap > ans) // 更新最大容积 ans = cap; /*排除容积不可能更大的情况*/ --right; while(height[right] <= cap_height && left < right) --right; } else{ // 取左边的高度为高 int cap_height = height[left]; int cap = (right - left) * cap_height; // 计算容积 if(cap > ans) // 更新最大容积 ans = cap; /*排除容积不可能更大的情况*/ ++left; while(height[left] <= cap_height && left < right) ++left; } } return ans; } }
-
- 分别用两个指针p1, p2标识0的右边界和2的左边界
- 使用curr从p1位置从左到右遍历
- 遇到0: 将该数字与p1处的数字交换, p1++, curr++(因为此时p1处交换过来的值定为1)
- 遇到1: curr++
- 遇到2: curr处数字与p2处交换, p2--, (curr不能右移, 因为不清楚交换过来的数字是多少, 需要再次判断)
class Solution { public void sortColors(int[] nums) { int p1, p2, curr; p1 = 0; p2 = nums.length-1; int tmp; curr = p1; while(curr<=p2) { if(nums[curr] == 0) { tmp = nums[curr]; nums[curr++] = nums[p1]; nums[p1++] = tmp; } else if(nums[curr] == 2) { tmp = nums[curr]; nums[curr] = nums[p2]; nums[p2] = tmp; p2--; } else{ curr++; } } } }
-
-
利用滑动窗口思想, 双指针, 左边指针进行遍历, 右边指针向右延伸到无重复的最远端, 每次迭代都更新最长子串的max值, 一次遍历结束后取消左指针所指向的字符占用
/* 此题使用了 char[] 结构, 并没有包括所有的字符情况, 由于测试用例的原因通过了, 但是实际上最好使用map来保证所有的字符都能够被记录 */ class Solution { public int lengthOfLongestSubstring(String s) { if(s.equals("")) return 0; int len = s.length(); char[] strArray = s.toCharArray(); int[] words = new int[128]; int right = -1; int max = 1; for(int left=0; left<len; left++) { while(right<len-1 && words[strArray[right+1]-' '] != 1) { ++words[strArray[right+1]-' ']; ++right; } max = Math.max(max, right - left + 1); words[strArray[left]-' '] = 0; } return max; } }
-
-
-
排序后遍历第一个, 利用双指针指向第一个后面部分的最前和最后位置, 根据目标值的大小判断更新左或右指针
class Solution { public List<List<Integer>> threeSum(int[] nums) { List<List<Integer>> res = new ArrayList<List<Integer>>(); Arrays.sort(nums); // 排序 int len = nums.length; // 获取长度 if (len == 0) return res; if (nums[0]<=0 && nums[len-1]>=0) { // 排除数组中清一色是同一个符号情况 for (int i=0; i<len-2;i++) { // 注意! 这里不用递增 i , 在循环末尾会找到下一个和当前元素不同的元素 if (nums[i]>0) break; // 当首个数大于 0 的时候则说明后面的数也都肯定大于 0 了, 不可能产生和为0的情况了 if(i>0 && nums[i] == nums[i-1]) continue; int first = i+1; // 第二个元素 int last = len-1; // 第三个元素 while(first < last ) { // 开始查找合法的二三个元素 int result = nums[i] + nums[first] + nums[last]; // 获取结果 if (result == 0) { // List<Integer> tmpArr = new ArrayList<Integer>(); // tmpArr.add(nums[i]); // tmpArr.add(nums[first]); // tmpArr.add(nums[last]); // res.add(tmpArr); res.add(Arrays.asList(nums[i], nums[first], nums[last])); // 此方法比上面的分步骤运行会更快 } if (result <= 0 ) { //右移弱的 while(first < last && nums[first] == nums[++first]){}; } else{ // 左移强的 while(first < last && nums[last] == nums[--last]){}; } } } } return res; } }
-
-
给出方程式 A / B = k, 其中 A 和 B 均为用字符串表示的变量, k 是一个浮点型数字。根据已知方程式求解问题,并返回计算结果。如果结果不存在,则返回 -1.0。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/evaluate-division 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-
构建一颗树, 子节点除以父节点 = val[子节点]
-
构建的过程中, 若两个节点都存在且不在同一颗数上, 则进行合并
假设 root1 是 a 的根节点, root2 是 b 的根节点, 且 root1 != root2, 则由
root1 / root2 = a / b * val.get(b) / val.get(a) , 可使得
root1.parent = root2; val[root1] = a / b * val[b] / val[a]
-
最后依次计算, 如果要查询的 from 和 to 有一个不在 森林里面 或者 form 和 to 不在同一颗树中(根节点不同), 则无结果;否则计算 val.get(a) / val.get(b) 就得到了结果, 因为 find() 函数查找根的过程会将节点的"父指针"指向根节点, val.get(x)的值设置成当前节点与根节点的比值。
class Solution { private Map<String, String> parents; private Map<String, Double> val; private String find(String x) { // 查找根, 并将当前节点的父节点设置为根节点 if(!parents.get(x).equals(x)) { String tmpParient = parents.get(x); String root = find(tmpParient); // 递归 double oldVal = val.get(x); val.put(x, oldVal * val.get(tmpParient)); parents.put(x, root); } return parents.get(x); } public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) { parents = new HashMap<>(); val = new HashMap<>(); int i = 0; double cur; for(List<String> equation:equations) { // 构建树 String from = equation.get(0); String to = equation.get(1); cur = values[i]; if (!parents.containsKey(from) && !parents.containsKey(to)) { parents.put(to, to); val.put(to, 1.0); parents.put(from, to); val.put(from, cur); } else if (!parents.containsKey(from)) { parents.put(from, to); val.put(from, cur); } else if (!parents.containsKey(to)) { parents.put(to, from); val.put(to, 1/cur); } else { String pa = find(from); String pb = find(to); if(!pa.equals(pb)) { parents.put(pa, pb); val.put(pa, cur * val.get(to) / val.get(from)); } } i++; } i = 0; double[] res = new double[queries.size()]; for(List<String> query:queries) { // 开始计算 String from = query.get(0); String to = query.get(1); if(!parents.containsKey(from) || !parents.containsKey(to)) { res[i++] = -1; continue; } String pa = find(from); String pb = find(to); if(!pa.equals(pb)) { res[i++] = -1; }else{ res[i++] = val.get(from) / val.get(to); } } return res; } }
-
-
- 法一: 利用队列进行拓扑排序
- 法二: 利用dfs查找, 头尾相同的便是环
-
- 利用双向链表+哈希表
- 双向链表用于更新维护最新被使用的节点
-
- 利用字符串序列化
- StringBuilder
- 递归调用
- 利用字符串序列化
-
class Solution { private List<Integer> l = new ArrayList<>(); public List<Integer> findAnagrams(String s, String p) { char[] cs = s.toCharArray(); // 将 s 转为字符数组 char[] cp = p.toCharArray(); // 将 p 转为字符数组 int[] winFreq = new int[128]; // 滑动窗口的字符出现频率表 int[] pFreq = new int[128]; // 字符串数组的字符串出现频率表 int left = 0; // 滑动窗口左边界 int right = 0; // 滑动窗口右边界 for(int i=0; i<cp.length; i++) { // 初始化 p 字符串的字符频率表 pFreq[cp[i] - 'a']++; } while(right < cs.length) { // 开始查找过程, 条件是 右边界没有超出 cs 的长度 int indexR = cs[right] - 'a'; // 获取滑动窗口右边界对应的字符相对于 'a' 的偏移 right++; // 右边界右移一位 winFreq[indexR]++; // 前右边界对应的字符出现频率 + 1 while(winFreq[indexR] > pFreq[indexR]) { // 当右边界字符在窗口表的出现频率大于p的时候, 需要将滑动窗口的左边界右移 int indexL = cs[left] - 'a'; // 得到左边界对应的字符偏移下标 left++; // 滑动窗口左边界右移一位 winFreq[indexL]--; // 滑动窗口字符频率表中左边界字符对应的频率 - 1 } if(right - left == cp.length) // 在满足上述可能出现合法情况的条件下, 若再满足子串长度相同的条件, 则可以判定该情况符合题意, 将左边界添加到答案数组中去. l.add(left); } return l; } }
-
76. 最小覆盖子串 ****
- 利用128位数组作为map来映射字符
- 使用distasnce来计算是否满足子串条件
- 先动右边,满足条件了再缩小左边, 看最小能缩小到多少, 记录下来
-
- 利用哈希表去重, 但用数组可能会更快(26位字符的偏移)
-
-
法一: 暴力遍历
-
法二: 前缀和 + 哈希表
public class Solution { public int subarraySum(int[] nums, int k) { Map<Integer, Integer> pre = new HashMap(); int ans = 0, sum = 0; pre.put(0,1); // 此状态很重要, 当从第一项开始计算的和正好等于k的时候需要用该记录来添加匹配项 for(int i=0; i<nums.length; i++) { sum += nums[i]; if(pre.containsKey(sum - k)) // ans 的计算一定要在添加新的key之前 , 否则新添加的键值对数据将会使得ans的计算产生错误. 原因是 ans 添加的必须得是不算当前数字的之前的所有前缀和的情况, 而加上当前数据后便无法做出准确判断了. ans += pre.get(sum - k); if(pre.containsKey(sum)) pre.put(sum, pre.get(sum) + 1); else pre.put(sum, 1); // pre.put(sum, pre.getOrDefault(sum, 0) + 1); } return ans; } }
-