v.0.0.1

README.md

@@ -1,2 +1,35 @@
 # FastCubicSplineInterpolation
-fast cubic spline interpolation in Java and Matlab
+This repository contains fast cubic spline interpolation written in Java and Matlab, implementing code from the paper of Haysn Hornbeck "[Fast Cubic Spline Interpolation](https://arxiv.org/abs/2001.09253)".  
+The original python code is available [here](https://doi.org/10.5281/zenodo.3611922).
+The motivation for this code is described in the paper, but basically it is [Creative Commons Zero license](https://creativecommons.org/publicdomain/zero/1.0/) analogue of *Numerical Recipes* procedure.
+
+## General idea
+The general idea behind is that given *N* tabulated knots *x<sub>i</sub>* (*x<sub>0</sub>*,*x<sub>1</sub>*,...,*x<sub>N-1</sub>* so that *x<sub>0</sub>*<*x<sub>1</sub>*<...<*x<sub>N-1</sub>*)   
+and function values *y<sub>i</sub>* at those points, code builds [interpolating](https://en.wikipedia.org/wiki/Interpolation) piece-wise cubic spline passing through those points.  
+This interpolation is smooth in first derivative and continuous in the second derivative.  
+(*BTW, for a general spline "getting started" I highly recommend [this great video](https://www.youtube.com/watch?v=jvPPXbo87ds)*).
+
+To build this interpolation, one of the two extra assumptions at boundaries are needed:
+1. The second derivatives at the end points are equal to zero (functions *CubicSpline(x,y)* in java and *cubicspline(x,y,xs)* in matlab). In this case it is so called *natural* cubic spline. Or
+2. The first derivatives at the end points are provided by user (functions *CubicSpline(x,y,start_deriv,end_deriv)* in java and *cubicspline(x,y,start_deriv,end_deriv,xs)* in matlab).  
+
+Well, in practice, it is possilbe to mix them: for one end second derivative is zero and specify derivative for the second end. Then for the first end just supply a large (*Double.MAX* or *Inf*) value of the first derivative.
+
+## Additional functions
+This code is actually a bit extended version. There are two additions:
+1. There is a possibility to estimate first derivatives from the provided data at end points. Calling functions *CubicSpline(x,y,n_est)* in java and *cubicspline(x,y,n_est,xs)* in matlab estimates derivatives values using *n_est* boundary points for each end. It is done by [finite difference](https://en.wikipedia.org/wiki/Finite_difference_method) method, where coefficients are calculated from [this paper](https://doi.org/10.1090%2FS0025-5718-1988-0935077-0). The *x<sub>i</sub>* values does **not** have to be equidistant.
+2. Apart from evaluation of spline itself at interpolation points, there is a new routine to calculate spline's derivative (slope) at those points (*evalSlope* functions).
+
+Some extra notes:
+## Matlab
+The usage of code is illustrated in "example.m" file. Here is interpolation with natural vs estimated first derivatives:
+![spline interpolation example](https://katpyxa.info/software/FastCubicSplineInterpolation/spline_fit.png)  
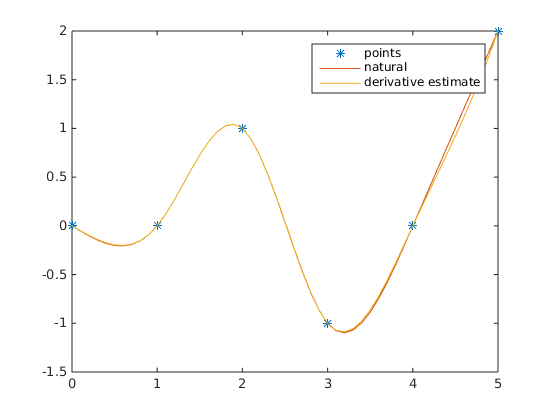+And calculated slopes (derivatives, tangents) shown as arrows on top of the second spline:  
+![slope calculation example](https://katpyxa.info/software/FastCubicSplineInterpolation/spline_deriv.png)  
+
+## Java
+
+The main package/class is *cubicspline/CubicSpline*. This repo also contains comparison of this implementation with the one used in ImageJ (*cubicsplineIJ/CubicSplineImageJ*). And *test* package to validate main class against Matlab/ImageJ routines.
+
+---
+Email katpyxa @ gmail.com for any questions/comments/suggestions.