Információ és kódelmélet

Követelmények:

• 2 zh 25 pt a max
• beadandó (15pt) és annak prezentálása (5 perc)
  • elmúlt max 3 évben publikált technika alkalmazaása
  • néhány oldalas esszé, 2-10 oldal, forrás megjelöléssel
  • kódelmélet/titkosítás/tömörítés technika
• félévközi kis házi feladatok (35pt)

EA1

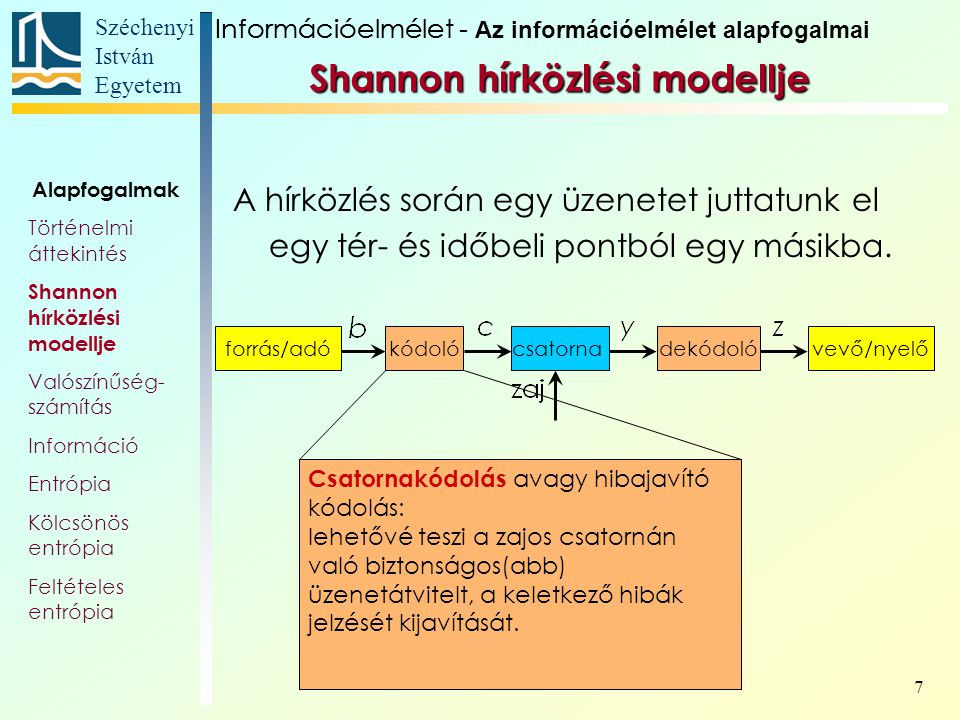
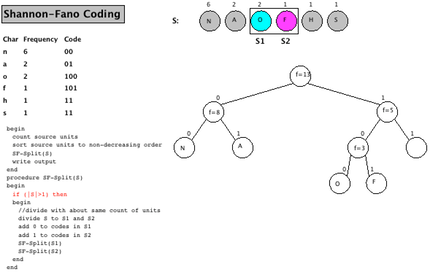
Kódok

• Speciális jelentéssel bíró szavak, betűk, színek, jelek
• Nem minden kód titkos.
• A napi gyakorlatban a kódokat gyors és könnyű üzenetküldésre használjuk (szemafor, Morse-kód, térkép kódok, bináris kódok,…)

A kriptológia a rejtett, vagy titkos kommunikáció tudománya és felöleli mindazokat a módszereket, amelyekkel olyan üzeneteket lehet készíteni, amit csak az arra jogosultak tudnak megfejteni.

A kódoláselmélet olyan algoritmusok keresésének a tudománya, amelyekkel a digitális információt hatékonyan kódolhatjuk zajos csatornákon történő megbízható átvitelhez. nem feltétlen titkosítás!

Az információelmélet az üzenetek adásának és vételének (kommunikációnak) matematikai elmélete.

Története

• 1837: S. Morse elektromos távirója és kódja
• 1875: E. Baudot jeltovábbítója és kódja
• 1924, 1928: H. Nyquist és R. Hartley munkái a kommunikációs csatornákról és az átviteli sebességről, American Telephone and Telegraph Company-Bell laboratórium
• 1947-1948: Az információelmélet születése: C. Shannon forráskódolási és csatornakapacitási tételei.

Shannon szerint az optimális csatorna felhasználási kapacitást a Shanon kóddal adhatjuk meg ami az üzenetben nézi a szavak eloszlását és rövidebb szóhoz/betűhöz rövidebb kódot ad hosszabbhoz, hosszabbat, hogy a végeredmény egyenletes legyen.

Alapfogalmak:

• információ: véges számú ismert lehetséges alternatíva valamelyikének megnevezése. Azt vizsgáljuk, hogy mennyi "információ" kell egy tetszőleges elem azonosításához, ha az alternatívák lehetséges A halmaza adott.
  • hír: tudom mi a téma és azzal kapcsolatban várok új információt
• Forrás: az információt(közleményeket) szolgáltató objektum.
• Forrásábécé: véges jel halmaz (ábécé) (pl a magyar/angol ábécé)
• közlemény: a forrásábécé jeleiből álló véges jelsorozat
• távközlési csatorna: egynelő időközönként egymás után következő jelek vihetőek át rajta
• csatornaábécé: a gyatornán továbbítható kódjelek összessége (csatornán továbbítható jel lehet pl 1/0)
• lehetséges kódtípusok: változó hosszúságú/fix hosszúságú blokk kód
• lehetséges kódolási eljárás: betűnként/blokkonként,veszteséggel vagy a nélkül példák: Morse kód, Ascii kód, isbn kód
• Zajmentes csatorna: ideális, a jeleket nem torzítja, a kimeneti kódjel mindig ugyanaz mint a bemeneti
• Zajos csatorna: a jeleket torzít(hat)ja
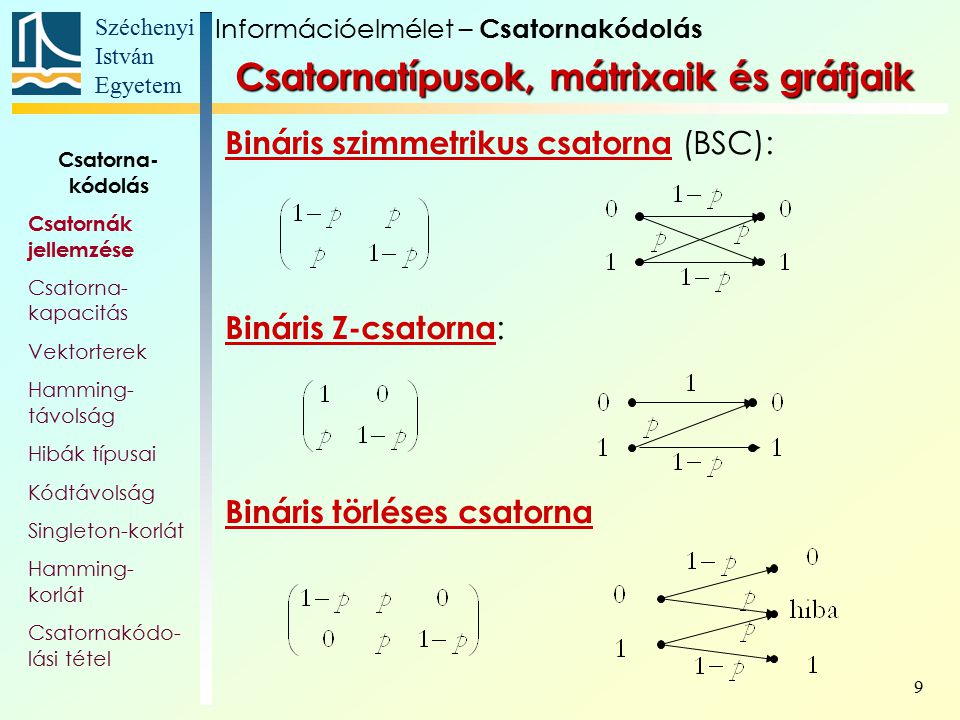
• Bináris csatorna: kétféle kódjel továbbítható rajta
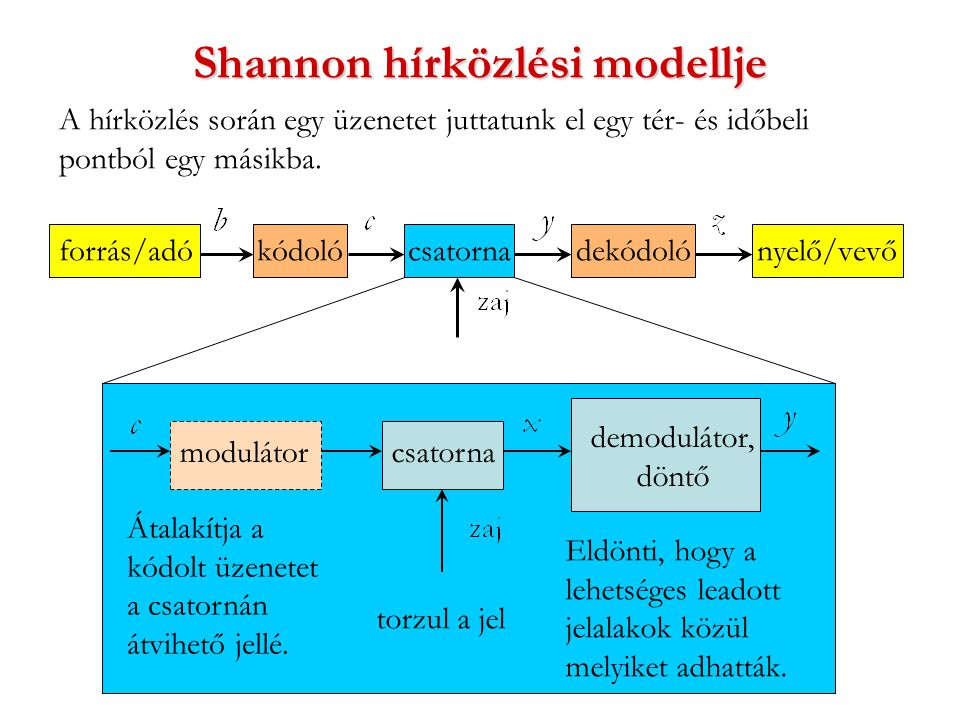
• Kódoló: a közleményt átalakítja a csatornán való továbbításhoz (kódolás)
• Kódközlemény: az eredeti közlemény kódolt alakja, a csatornaábécé "betűiből" álló véges sorozatok
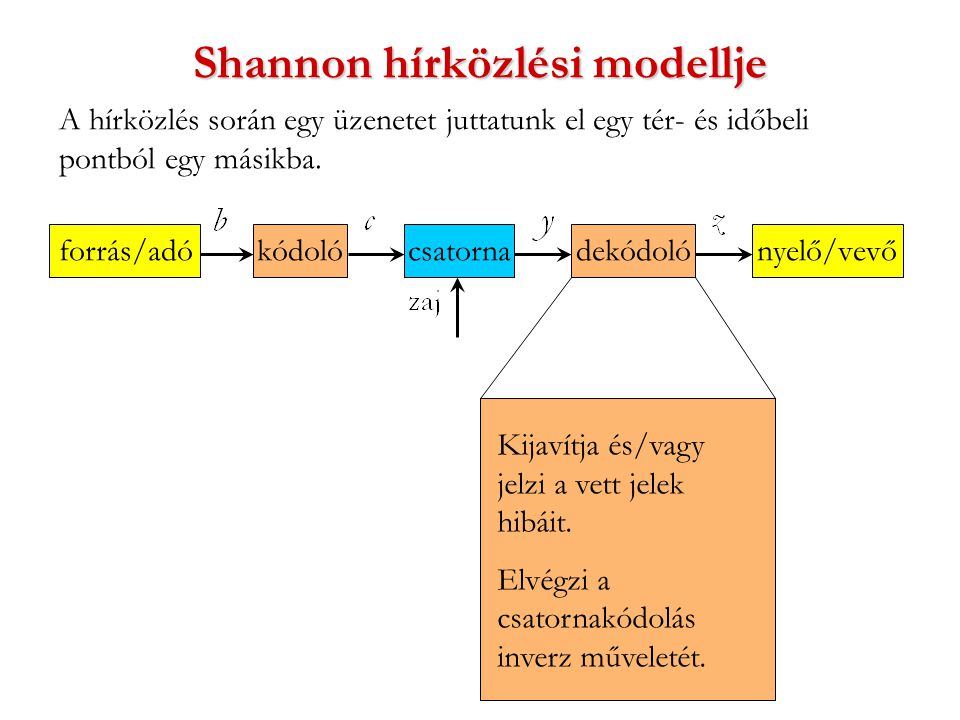
• Dekódoló: a csatorna kimeneti oldalán vett (kód)közlemény megfejtése (dekódolás)
• Kódolási eljárás: olyan "utasítás„/algoritmus, amely minden lehetséges közleményhez hozzárendel egy kódjelekből álló sorozatot, az illető közlemény kódközleményét

Lehetséges kódolási eljárások:

• betűnként, blokkokként,
• információ veszteség nélkül, információ veszteséggel

Lehetséges kódtípusok:

• változó hosszúságú Példa: Morse-kód
• fix hosszúságú (blokk) kód.
  • Példák:
    • Baudot-kód (5 bites blokkok),
    • ASCII kód (8 bites blokkok),
    • ISBN kód (10 jel hosszú blokkok)

Definíció: Egy kód blokk kód, ha a kódok a csatornaábécé fix hosszúságú sorozataiból állnak.

Tételek

http://zeus.nyf.hu/~falu/kod/k.pdf, fájlként: https://github.com/gabboraron/informacio_es_kodelmelet/blob/main/kodelmelet.pdf

Az A1, A2,..., An nemüres halmazok Descartes vagy direkt szorzatán az X[i=1 → n] Ai = A1 x A2 x ... x An = {(a1, a2, ..., an) | a1∈A1, a2∈A2, ..., an∈An} halmazt értjük.

Legyen továbbá A ≠ ∅, A^n = A x A x ... x A (n-szer A) = A^+ = ∪A^n | n>=1.

Tetszőleges Σ ≠ ∅ halmazt ábécének nevezzük. A Σ ábécé elemeit a Σ betűinek (szimbólumainak) nevezzük. Példa: Σbool = {0,1}, a Boole ábécé; Σlat = {a,b,c,...,z} a latin ábécé.

Def: A Σ ábécé jeleinek tetszőleges véges sorozatát Σ feletti szónak nevezzük. A w szó, |w| hossza a w-ben lévő jelek száma. A w = x1x2...xn szó hossza: |w| = n. A w szót felfoghatjuk a Σn halmazz egy (x1, x2, ..., xn) elemeinek is amelyből a zárójeleket és az elválasztójeleket elhagyjuk.

Def: Σ+ a Σ ábécéből képzett összes szó halmaza. A továbbiakban jelöljön Σx = {x1, x2, ..., xd} egy forrásábécét Σy = {y1, y2, ..., yr} pedig egy csatornaábécét!

Betűnkénti vagy szimbólum kód: A K: Σx → Σy+ leképezést kódnak nevezzük, a K(x) az x ∈ Σx-hez tartozó kódszó, l(x) a K(x) kódszó hossza, Li = l(xi). Állandó n hosszúságú kód esetén K valójában K:Σx → Σyn típusú leképezés, ahol n az állandó (blokk) kódhossz. A kódot szokás a K={K1, K2,...Kd} lakban is megadni, ahol a Ki ∈ Σyn az xi ∈ Σx szimbólumhoz rendelt kódszó.

Változó hosszúságú betűnkénti kódoláshoz minden egyes jelet megszorzunk a jel gyakoriságával és ezek összegét vesszük.

Kiterjesztett K+ kód: Az K+: Σx+ → Σy+ leképzeést a K kód kiterjesztésének nevezzzük, ha K+(xi1xi2...xiN) = K(xi1)K(xi2)...K(xiN). Gyakorlatban a K+ jelölés helyett a K(xi1xi2...xiN) = K(xi1)K(xi2)...K(xiN)-t használjuk.

Def: Egy K: Σx+ → Σy+ kódot nemszingulárisnak nevezünk, ha minden x,x' ∈ Σx, x ≠ x' esetén K(x) ≠ K(x') is teljesül. A nemszingularitás elég egy kódjel egyértelmű azonosításához, de nem elég egy üzenet azonosításához.

szinguláris kód: minden ábécéhez ugyanazt rendeljük

Def: Egy K: Σx+ → Σy+ kód egyértelműen dekódolható, ha Σx+ különböző elemeit (üzeneteket) különböző karaktersorozatba képezi, azaz ∀x,y ∈ Σx+, x≠y ⇒ K+(x) ≠ K+(y). Azaz K+ invertálható. Zajmentes csatorna esetében az egyértelmű dekódolhatóság biztosítja az információ hű átvitelét.

Def: Egy kódot prefixnek nevezünk, ha egyetlen kódszó sem valódi szelete egy másiknak. Minden prefix kód egyértelműen dekódolható. Biz: Tfh két Ki1Ki2...Kin és Kj1Kj2...Kjm jelsorozat megegyezik, azaz Ki1Ki2...Kin = Kj1Kj2...Kjm. Igazoljuk, hogy Ki1 = Kji. Ha Li1 = Lj1 akkor a két közlemény jelenkénti egyenlősége és a kódszavak különbözősége miatt meg kell, hogy egyezzenek. Ha az egyik kódszó hosszabb volna a másiknál, akkor az szükségképpen a másikfolytatása. De ez a prefx tulajdonság miatt nem lehetséges. Tehát Ki1 = Kj1. A gondolatmenetet í]y folytatva kapjuk, hogy a Kil = Kjl (l>1) és m=n.

Σx	a - szinguláris	b - nem szinguláris nem egyértelműen felírható prefixkód	g - egyértelműen dekódolható, de nem prefix	d- prefix kód, egyiknek sem folytatása a másik kód, és egyértelműen dekódolható	o - egyenlő hosszúságú kódokat is hozzá lehet tenni, mivel négy jelet kódolok ezért a kódhozz 2
1	0	0	10	0	00
2	0	010	00	10	01
3	0	01	11	110	10
4	0	10	110	111	11

Gazdaságosság

Tekintsük először az állandó hosszúságú betűnkénti kódolás esetét bináris csatornaábécét és egyértelmű dekódolhatóságot feltétlezve. A kódjelek hosza L. Ekkor N jel hosszúságú közlemény továbbításának költésge N L-el arányos egy betű átlagos költsége peig C=(1/N)NL = L. Az L hosszúságú 0 - 1 sorozatok száma 2^L. A d betűhöz 2^L különböző L bit hosszú bináris sorozat rendelhető. Egyértelműen dekódolható, ha d<=2^L ⇔ log3 d <= L. Tehát L = log3 d felülre kerkekítésével.

Állandó kódhosszúságú és egyértelműen dekódolható bináris kódlásnál az egy betűre eső költésg log2d-nél nem lehet kisebb: log2d≤C<log2d+(1/n) ha az egy betűre jutó költség C.

Változó betűnkénti kódhosszúság esetén a gyakoribb jelnek hosszabb kódot adunk, a legrövidebb közleményt a legrövidebb módon szeretnénk tárolni. Ehhez minden jelhez kell annak a valószínűsége. Σx = {x1, x2, ..., xn} a forrásábécé, pi az xi előfordulásnak a valószínűsége. Ki az xi kódja, Li pedig xi kódjának hossza. A teljes hossz: L = Σ [i=1 → d] NiLi Az egy betűre eső átlagos kódhossz: L' = L/N = Σ[i=1 → d](Ni*Li)/N. Azaz az előforduló jelek relatív gyakoriságukkal megszorozva: L(K) = Σ[i=1→d]Ni*pi.

EA2 - forráskódolás

• https://forgos.uni-eszterhazy.hu/wp-content/tananyagok/tarsesmedkomm_pc_exe/415_shannon_s_weaver_informcielmleti_hradstechnikai_modellje.html
• információs rendszerek alapjai, fájl: Információelmélet - molnarba - ELTE.pdf

Információmennyiség

Információ valamaly véges számú, előre ismert esemény közül annak megnevezése, hogy melyik következett be. Alternatív megfoglamazás: az infomráció mértéke azonos azzal a bizonytalansággal amelyet megszűntet.

Felező algoritmus: mindig felezzük az intervallumot, és így kapjuk meg a keresett elemet, azaz 8 elemből 3 lpéssel kapjuk meg az elemet. Azaz 8=2^3 amiből 3 lépésben kaptuk meg, tehát kettes alapú logaritumst használva kapjuk meg a lépésszámot. Amennyiben nem kettővel osztható, úgy felső egész részét vehetjük a logaritmusnak.

Hartley: m számmú azonos valósínűségű esemény közül egy megnevezésével nyert infomráció: I=log2m. (Azaz log2m kérdéssel azonosítható egy elem). Két esemény összevonsával 1 bittel lesz rövidebb, hiszen m/2 számú párból egy. Ez ugyanaz mint I = -log1/m

Shannon: minél váratlanabb egy esemény bekövetkezése annál több infomrációt jelent, annál több bizonytalanságot kell kiküszöbölni. Legyen A={A1, A2, ..., Am} esemény halmaz, m eseménnyel az A1 esemény valószínűsége p1, ... az Am-é pm. Ekkor Ai megnvezésekor nyert irnformáció: I(Ai) = log21/pi=-log2pi.

információ mennyiség:

• keresett jel gyakorisága/(összes jel gyakoriságának összege, ez m
• m számú azonos valségű esemény közül egy megnevezésével nyert információ I = log2*m*

normálás: legyen I(A)=1 ha p(A)=1/2=0,5. Azaz, ha az infomráció mennyisége 1 akkor a hozzá tartozó valség 1/2. Ekkor kettes alapú logaritmus használandó és az információmennyisége a bit.I(mi)=log(1/pi). Ha 10-es laapú logaritmust használunk akkkor hartley-nek nevezzük, ha természetes alapú logaritmust használunk akkor nat.

példa:

• a forrás lead egy üzentet amiben van 21 db c, 22 dbn, 17 dbdakkor az információtartalma, ha a következő betű clesz úgy adható meg, hogy:
  • relatív gyakoriság:c darabszáma/összes elem száma azaz p(c) = 21/(21+22+17) = 21/60 = 0,35
  • hozzá tartozó infomráció mennyiség: -log2elem relatív gyakorisága azaz: l(c) = -log20,35 = -ln0,35/ln2 = 1,51

Csatorna kapacitás: adott csatornához a kapacitás- a bináris szimmetrikus csatornával való ekvivalencia alapján: Egységnyi idő alatt „átlag” ugyanannyi különböző jelsorozat vihető át, mint egy C bit/sec sebességű bináris csatornán. Ekkor a csatorna kapacitás C.

A forrás szimbólumok sorozatát választja, a választás bizonytalanságát jellemezzük az egy szimbólumra jutó átlagos mennyiséggel, ez lesz a Shannon-entrópia. Entrópia sázmoló: https://planetcalc.com/2476/

Shannon egy véges sok jelből álló (véges ábécé feletti) üzenet információértékét az üzenet jeleinek mint a jelre jellemző valószínűséggel bekövetkező események információtartalmának „átlagos”, azaz várható értékeként határozta meg: azaz az i-edik jelhez tartozó információ mennyiségéevel kifejezve az entrópia az a jelnekénti infomráció valószínűség és az elem gyakoriságának szorzatának elemenként vett öszege: . Az entrópia egy elem bizonytalanságának mértékével egyenlő. "Ha két jel azonos értékkel rendelkezik akkor az azt jelzi, hogy nehéz megjósolni a következő elemet.".

Entrópia tulajdonságai:

1. Nem negatív:  H( p1,p2,…,pm) ≥  0, ha pi = 1 akkor H(x)=0
2. Az események valószínűségeinek folytonos   függvénye.
3. H( p1,p2,…,pm, 0 )  =  H( p1,p2,…,pm)
4. Ha pi= 1, a többi  pk = 0, ( k=1, …, i−1, i+1 ,…, m), akkor  H( p1,p2,…,pm) = 0.
5. H( p1,p2,…,pm) ≤ H( 1/m,1/m, … 1/m ) Egyenlőség csak egyenletes eloszlásra, a legnagyobb  bizonytalanságú eloszlásra. 6.H(p1, …, pk−1,pℓ ,pk+1,…,pℓ−1,pk ,pℓ+1,…,pm) = H( p1,p2,…,pm), ∀k, ℓ ;   azaz az entrópia szimmetrikusváltozóinak cseréjére. 
6. szétválasztás: H(p1,…,pn) = H(p1+p2,p3,…,pn)+(p1+p2)H(p1/(p1+p2), p2/(p1+p2)).

K szimólum átlagos (várható) kódhossza: L(K) = Σp(xi)l(xi) | x∈Σx Azaz ez a relatív gyakorisága az elemnek.

teljes kódhossz: L(x) = nili + n2l2 + ... + ndld

átlagos kódhossz: L(x) = (nili + n2l2 + ... + ndld)/n

• rövid kódhoz a legnagoybb valséget rendeli
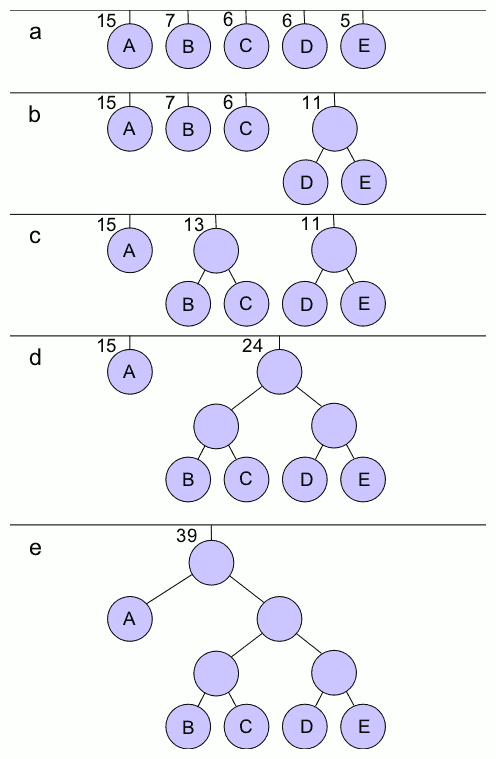
  • huffman kód viszafele halad

Kraft-Fano egyenlőtlenség: 4.30-as tétel: Információ- és kódelmélet - Fegyverneki Sándor - Miskolc.pdf, vagy: https://www.uni-miskolc.hu/~matfs/INF_11_main_kep.pdf

McMillan egyenlőtlenség: akkor is fenn áll ha egyértelműen dekódolhatóak, nem csak a prefix kódra: Ha a forrás ábécé: és a kódolt szavak hossza rendre , mikora kód r akkor .

Prefix kód alsó határa:

• forrásábécé: Σx = {x1, x2, ..., xd}
• eloszlása: Px = {p1, p2, ... pd}
• csatornaábécé: Σy = {y1, y2, ..., yd}
• prefix kódja: K = {K1, K2, .... Kd} ahol Ki kódszó hossza Li
• ekkor: L(K) = ΣLipi ≥ H(x)/log2r | i=1..d Azaz az átlagos kódhosssz nagyobb vagy egyenlő mint az entrópia, egyenlő, ha a kódhossz a kitevők számát adja.
• Optimális forráskódhossz: Li = logr(1/pi)

Prefix kód felső határa: L(K) < (H(X)/log2r)+1

Kód hatásfoka: H(x)/(L(K)log2r)

Huffamnn kódolás: https://hu.wikipedia.org/wiki/Huffman-k%C3%B3dol%C3%A1s

• prefix
• optimális

Lépések:

• a két legkisebb valószínűségű elemet összevonjuk
• ezt elvégezzük az összes elemre
• újrarendezzük
• ismétlejük
• ...
• amire származtattunk arra 0-t adunk, amire nem arra 1-et, ezt folytatjuk visszafele

YT tutorial: https://www.youtube.com/watch?v=A6wEgIVEZL8

bővebben: Algoritmusok es adatszerkezetek 2 javitott 2019.06.07.pdf

• Huffman-kódolás wikipédiában

  • https://people.ok.ubc.ca/ylucet/DS/Huffman.html

• Előnye hogy rövidebb.

EA3 - elmaradt

EA4 - statisztikai alapú kódolás

Shannon-Fano kód

• Informatika alapjai jegyzet -Tóthné Dr Laufer Edit.pdf - 105 - oldal
• Shannon-Fano kód: hivatalos jegyzetben: http://siva.bgk.uni-obuda.hu/~laufer/bevinfo_tankonyv/Informatika%20alapjai%20jegyzet.pdf
  • Kutor féle részlet

Lépések:

1. rendezzük gyakoriság szerint
2. felmérjük egy [0,1] intervallumra, úgy, ohgy a lgekisebb van elől az 1-nél
3. Az intervallumot felosztjuk egyenlő részekre, ezt addig ismételjük míg minden elemhez tartozik egy intervallum szakasz.
4. a szakaszokból kkódfár építünk, balra 0 jobbra 1 elágazással.

|x2        x4      x3    x1   x5   |
0                                  1
[               ][                 ]
                 [        ][       ]
                 [    ][  ][  ][   ]
        x2          x4   x3 x1   x5
        
                /\
               0  1
                  /\
                 0  1
                /\  /\
               0  1 0 1
x1 = 110
x2 = 0
x3 = 101
x4 = 100
x5 = 111

Gilbert-Moore kód

• Informatika alapjai jegyzet -Tóthné Dr Laufer Edit.pdf - 108 - oldal
• Gilbert-Moore kód Azért jó mert nem kell rendezni, hanem olyan sorrendben vesszük fel az intervallumra ahogy jönnek az elemek, így lesznek üres ágak, de a kód nem lesz optimális.

Optimális kód tulajdonságai

Az a kód ami a legjobban megközleíti az átlagos kódhossz alsó határát.

1. Ha növekvő sorrendben állnak a valószínűségek akkor csökkenő sorrendben állnak a hozzájuk tartozó kódhosszok, ugyanaz a rendezettség kell legyen
2. kiegynesúlyozott kódfát kell kapnunk.

Távközlési csatorna

Diszkrét emlékezet nélkül csatorna

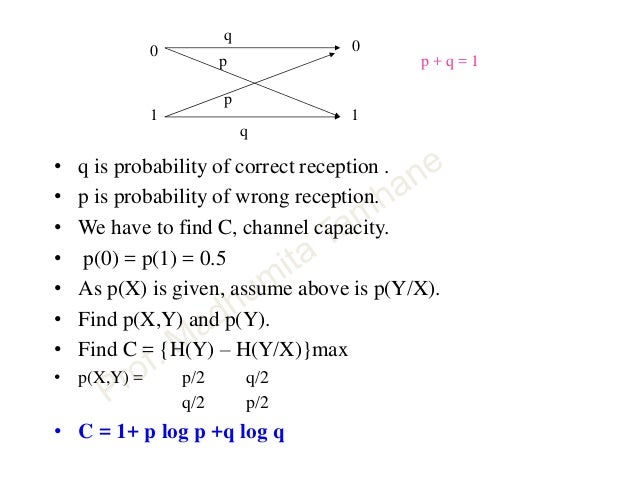
P(y|x) ~ y- t fogadtunk és x-et küldtünk.

A csatorna az átviteli valségek mátrixával jellemezhető: p(y|x) ahol x az input jele, y az output jele.

Ha X és Y val változók lehetséges értékei, azaz Σx = {x1, x2, ..., xr} és Σy = {y1, y2, ..., ym} Tegyük fel, hogy a csatorna hibázhat: xj imput jelhez több yj kimenet bármelyikét hozzárendelheti, p(x|y) annak a valsége, hogy y-t fogadtunk, úgy, hogy x-et küldtünk: p(x|y) = P(X = x|Y = y) = p(x,y)/p(y). Azaz p(x|y)*p(y) = p(x,y) tehát a peremvalószínűséget kifejezhetjük így is: p(x|y) = p(x,y)/p(y).

Perem és feltételes valószínűségek

mekkora a valsége annak, hogy y értéke 1

együttes valószínűségi csatornamátrix/táblázat:

P(x,y)    |        x               | P(y)
__________|___1____2_____3_____4___|_____
        1 |  1/8  1/16  1/32  1/32 |  1/4
        2 | 1/16  1/8   1/32  1/32 |  1/4
   y    3 | 1/16  1/16  1/16  1/16 |  1/4        
        4 | 1/4    0     0     0   |  1/4
__________|________________________|_____
  P(x)    | 1/2   1/4   1/8   1/8  |

x és y függetlenek, ha P(xi,yi) = P(xi) * P(yi) Ez alapján pl a fenti táblázatban, x = 2; y=2 esetben P(y) = 1/4, P(x) = 1/4 tehát P(xi,yi) = 1/4 * 1/4 = 1/16 de a táblázatban 1/8 szerepel, tehát ezek a val váltok nem függetlenek egymástól!

A feltételes valséghez: P(x|y) úgy jutunk, hogy minden x,y mátrix értéet elosztjuk a perem valószínűséggel, P(y)-al, teht pl, ha x =1; y=1 esetet vesszük akkor 1/8 az érték, amit elosztunk a hozzá tartozó P(y)-al, 1/4-el

P(x|y)    |       x
__________|__1____2____3____4__
        1 | 1/2  1/4  1/8  1/8
        2 | 1/4  1/2  1/8  1/8
   y    3 | 1/4  1/4  1/4  1/4
        4 |  1    0    0    0

*pl: Mekkora a valsée annak, hogy 2-t kapunk ha 3-mat küldünk?: y = 2; x = 3-ban 1/8, tehát 1/8 a valsége.

Feltételes entrópia és kölcsönös információ

https://vik.wiki/Felt%C3%A9teles_entr%C3%B3pia_%C3%A9s_tulajdons%C3%A1gai Annak az informáciuónak az átlagos mennyisége amly annak az x mértékének a megadásához súlyozottan ismertek.

X és y bizonytalansági mértéke a feltételes bizonytalanásgi mérték összegezve a feltétel bizonytalanságával H(x,y) = H(y) + H(x|y)

Ezért a H(x) - H(x|y) azt adja meg, hogy az y mennyi plusz információt ad x-ről.

Feltételes entrópia: H(X|Y = yk) = Σp(x|yk)log21/p(x|yk) | x∈Σx Az xentrópiája egy adott, fogadott y tükrében ezt a feltételes vaséget használja:p(x|yk), ezután minden y fogadott jel szerint ezt súlyzottan összegezzük, tehát minden fogadott entrópiát összegzünk a hozzá tartozó y súlyával: ΣΣp(x,y)log21/p(x|y) | x∈Σx; y∈Σy. Azaz az entrópia az esemény bekövetkezésének valószínűségének és az esemény információ tartalmának hányadosa. Alacsony valószínűséghez mgaas információtartalom társul, ismét.

x és y bozonytalansági mértéke: a feltételes bizonytalansági érték a feltétel bizonytalanságával megtoldva: H(x,y) = H(y) + H(x|y) = H(x) + H(y|x) tehát H(x|y)<=H(x)

x és y valvált kölcsönös információja: annak átlagos mértéke amit x és y egymásra vonatkozóan tartalmaz: I(x,y) = H(x) - H(x|y), azaz ez annak az indormáció mennyisége amit a fogadott jelkészlet nyújt (y), az elküldött jelkészletről(x`).

------------H(x,y)--------------
-------H(x)--------
           --------H(y)---------
--H(x|y)-- --I(x,y)-- --H(y|x)--  

Csatorna típusok

A csatorna zajmentes ha X=Y, ekkor I(x,y) = I(x,x) = H(x) <= log r

szimetrikus csatorna

A csatorna szimatrikus, ha a [p(y|x)] csatornamátrix sorai egymás permutációi és oszlopai is egymás permutációi.

pl szimetrikusra:

p   1-p       =      p(0|0)   p(1|0)
1-p  p               p(0|1)   p(1|1)

pl aszimetrikusra:

1-q   0             
q     q        =     
0     1-q

EA5

csatorna kapacitás

A csatornakapcitás emlékezet élküli csatornán: C = max I(x,y)

Shannon szerint: a csatorna kapacitás az egy kódjellel maximálisan átvihető információ átlagos értékével egyenlő. Ha a csatorna kapacitása C és a csatorna kód átlagos hossza L(K), akkor egy kódszó átlagosan L(K)C mennyiségű információt vihet át a csatornán. Ezért a forrás közleményeket csak akkor továbbíthatjuk, ha a H(X)<=L(K)C.

Bináris szimetrikus csatorna esetén a helyes továbbítás valsége p, a hibáé q=1-p.

https://www.slideshare.net/DrSanjayMGulhane/digital-communication-information-theory

EA6 - hibajelzés, hibajavítás

https://gyires.inf.unideb.hu/GyBITT/30/ch03s02.html

hogyan ismerjük fel a hibát és hogy tudjuk kijavítani?

miért:

• továbbításkor megváltozik az üzenet
• kibővítjük az eredeti üzenetet, hogy vételkor ellenőrizni tudjuk, történt-e változás
  • kód + redundáns információ
  • hibajelző újra küldés
  • paritás bitek
  • hibajavító kód, hamming kód, stb

Blokk kód

Egy adott elemhez egy blokknyi (azonos hosszúságú) kódot rendelünk. Alapvetően m adatbit, hozzátéve még redundáns bitet , most három ilyent. Ha nem adunk hozzá redundáns bitet akkor egy szisztematikus kód.

Lineáris kódok

A kód első részének valamilyen lineáris vag yvalamilyen más függvénye, mint a kizáró vagy vagy mod 2.

jellemzője ű

• kódhosszúság: ami a teljes kódra vonatkozik
• kódsebesség: azaz a nem redundáns információt tartlmazó rész m/n. Zajos csatornán sok redundáns bit kell.

Hiba

elküldök egy jelet és másikat fogadok. a köztük levő különbség a Hamming távolság.

Pl:

10001001
10110001
00111000

• első szó Hamming ávosága dH, jelen esetben 3
• a teljes kódrendszer Hamming rávolsága mindegyik kódszó mindegyikkel vett összehasonlításából keletkező érték minimuma.

hiba észlelése

Ha m hosszú a bináris üzenet akkor a lehetséges üzenet k száma 2^m, ezek legális kódszavak. az ellenörző bitek miatt nem fordul elő mindegyik kódszó, mert a redundáns rész ismétlődik.

Ha úgy választjuk kia a redundánsokat, hogy a kódszó leglaább 3 legyen akkor biztosan ki tudunk javítani egy bit tévedést.

Ha egy érvényes kódszót lát a vevő akor átviteli hiba történt. Ha viszont t hibát szeretnénk jelezni akkor 2*t+1 távolságú kell legyen, hogy felismerjük a hibát, hogy biztosan elkülönítsük kettőt egymástól. Ha csak 2t a különbség akkor a határon levő elemet nem lehet megmondani hova tartozik.

pl:

n=10

0000000000
0000011111
1111100000
1111111111

dh= 5, d = 5
5 = 2*t+1=> t = 2

Egy kód akkor és csak akkor korrekt t hibáig ha a kódtávolság >= 2t+1

A blokk három fő paramétere:

• M: kódvektorok száma
• n kódszavak hossza
• d kódtávolság

Az m paraméter helyett szokás az információs bitek k számát vagy az R=k/n hányadpst is használni. Szokás továbbá a blokk kódra az (n,M,d) formában hivatkozni.

Tetszőleges legfeljebb t hibát javító blokk kdra fenn kell állnia a M * ΣC(n,i) <= 2^n | i=0..t

• Ahol egynelőség áll fenn ott perfeekt kódról van szó
• a kófdokat 2^n darab bináris vektorként és M darab t sugarú gömbbel a *"legszorosabb kitöltést biztosítják"**.

Csak három tökéletes kódoszt ály létezik:

• pűratlan hosszúságú
• Hamming kódok - 1 hibát javít
• Golay kód.

példa:

- bináris ismétlődő kód hossza 3
- a kód a jelet 3 szor megismétli
 - `0`  - `000`
 - `1`  - `111`
- a két kód távolsága: `dH((000),(111)) = 3`
- `din = 3`
- 3 hoszú bináris vektorok száma `2^3 = 8`, ezek egy 3D kocka egségoldalainak is meglelelnek.

• Plotkin korlát: bámrely blokk kódra tlejesül, hogy: M<= 2^(n-2d+2)d
• Gilbert korlát: ha a aparméterek kielégítik (M-1) ΣC(n,i) akor létezik ilyen tulajdonásgú blokk kód.
• Varshamov - Gilbert korlát: ha a aparméterek kielégítik M * ΣC(n-1,i) < 2^n | i=0..d-2 akor létezik ilyen tulajdonásgú blokk kód.

Shannon tétele alapján eléggé hoszú hibajavító kóddal tetetszőlegesen kis hibavalószínűség érhető el, ha a kódolt bitek átviteli sebessége kisebb mint a csatorna kapacitása. A hosszabb kóddal javul a hibajavító képessége, de nő a dekódolás bonyolultsága és ideje.

beadandóról:

még három óra és zh a a kódolásból és a tömörítésből.

• a beadandó mindegy milyen formában, de doc formátumban kell, amihez kell egy prezentáció, kb 6- 8 dia

EA7

https://szit.hu/doku.php?id=oktatas:kriptologia:kriptografia

Ismétlés

D a kódtávolság ami a két kód közti különbség száma, pl: 000 és 111 kód között a különbség 3 theát D=3. Valamint 2t+1 = D => t=1 ahol t a felismerhető hibák száma.

A forrás k hosszú, u=(u1,u2,...,uk) bináris üzenet melyet tekintsünk egyetlen forrásszónak - kíván eljuttatni hírközlési csatornán keresztül egy nyelőbe. a Kódoló az üzenetet egyn ≥ k hosszúságú c=(c1, c2,..., cn) bináris kódszóba képezi le. A csatornakimenetén egy n hosszúságú v=(v1,v2,...,vn) bináris vett szó jelenik meg.

Az u ami k hosszúságú szót kibővítjük a kódolás során c-re ami már n hosszúságú.

Tehát a hiba az elküldött és vett szavak közti különbség, a Hamming távolságuk azon pozíciók száma maiben különbözik u és v ez lesz t: t=d(c,v)

Elsősorban aznos hosszúságú kódokról lesz szó, tehát blokkkódokról. A kérdés hány elemet lehet lekódolni?: Ha k hosszú a szó akkor 2^k üzenetet tudok elkódolni.

Dekódoláshoz a vett v szóból, valamilyen döntési mechanizmus alapján egy c kódba kell leképezni, azaz, meg kell nézni, hogy van-e hiba, össze kell hasonlítani, az eredeti kódszóval.

gyakorlati példa:

C(5,2) kód az alábbi kódolás szerint:

      u        c

a    00      00000
b    01      01101
c    10      10110
d    11      11011


dekódolási táblázat első pár sora:
  v       c'    u'
00000   00000   00
10000   00000   00
01000   00000   00
11000   00000   00
00100   00000   00
10100   10110   10
01100   01101   01
11100   01101   01
00010   00000   00
10010   10110   10
 ...     ...    ...

Tehát, ha van négy elemünk, a,b,c,d amikhez fix hosszú kódokat adunk hozzá, és kiegészül v-re, tehát 01-> 01101. Ezek után két lehetőségünk van:

1. táblázatos módszer: Átküldjük előre, hogy amennyiben a meghatározott v jelet vesszük, úgy azt milyen c' jelbe dekódolja, aminek milyen u' az eredeti kódszava. Ekkor mindegy, hogy a fogadott v szó létezik-e az eredeti kódolási eljárásban keletkezett c kódok bármelyikével, ha azt kapjuk pl a csatornán, hogy10100 akkor az 10110-nak feleltethető meg, ami az 10 bináris jelen futó c betű. hátránya: hogy nagy tárkapacitást ígényel, pl: k=50 bitüzenethosszúság esetén 2^50 ~ 10^15 méretű a kód.
2. hibajelzés módszer: Ehhez használjuk, hogy a Hamming-távolság, vagy kódtávolság: dmin=min(d(c,c')) | c != c', c,c'∈C, előző példában ezdmin=3. Hasonlóan meghatározhatjuk, hogy a vett szó kódszó-e, ha a hibák sázma legfeljebb tés dmin>t akkor hiba esetén biztosan nem keletkizk téves kódszó!

Lineáris kdok

Hogyan konstruálható elegendő hosszúságú kód? Miért pont ezek a bővítések szerepelnek ezekhez a kdokhoz? pl00-hoz 00000?

Generátor mátrixot használunk, ahol, ahol lineárisan független vektrokból álló mátrixot használunk:

G =  10110
     01101

mátrixot a u mátrixal vett XOR (mod2)-a adja.

Def: c kód lineáris kód, ha a C halmaz lineáris tér, azaz ha minden c,c ∈ C' esetén c+c'∈C. Ennek megfelelően g1,g2,...gk C-beli vektorok a 2^k elemet tartlmazó lineáris tér egy bázisát adják, tehát testszőlegesen sok c∈C elem előállítható velük: c=Σuigi | i=1..k.

Szisztematikus kód: az a kód amiben szerepel az eredeti kódszó. pl a fenti példa ilyen.

paritás mátrix: A C lineáris kódhoz hozzárendelünk egy H(n-k)xn méretű bináris mátrixor amelynek az a tulajdonsága, hogy detektálni tudja az n hosszú vektorok 2^n méretű halmazában a C kódszavait. A detektálás alapja: Hc^T =0 akkor és csak akkor igaz, ha c∈C. Szimetrikus ggeometrikus kódok esettén egyszerűen megkaphatjuk a H mátrixot: H=(A,In-k), ahol A=-B^T.

hibavektor: e=v-c ahol c a küldött, v a fogadott szó, pl: c=10110 és v=11110 akkor e=01000, azaz a második koordináta a hibás. Hasonlóan mátrixokra is a paritásmátrixal: Hv^T=H(c+e)^T=Hc^T+He^T=He^T.

Megadható a lineáris kódok dekódolása a szindráma felasználásával:

• két oszlopot írunk fel
• egyikben a szindrómák, másikban a szindrómáknak megfelelő minimális hibaszámú hibavektorok állnak.
• a nulladik sorban a zérus szindróma és a neki megfelelő zérus hibaminta áll ami hibamentes esetnek felel meg.

A szindrómavektorok hossza n-k, a szindrómák száma 2^n-k.

Szindrómadetektálás lépései:

1. a v vett szónak megfelelő s szindróma kiszámítása
2. a dekódolótáblázat s-nek megfelelő sorából a becsült ehibavektor kiolvasása
3. c'=v-e dekódolási lépés elvégzése
4. az u'dekódolt üzenet c'-hez rendelése

Paritás kód

https://hu.qaz.wiki/wiki/Multidimensional_parity-check_code

A kétdimenziós paritásellenőrző kód, amelyet általában optimális téglalap alakú kódnak neveznek, a többdimenziós paritásellenőrző kód legnépszerűbb formája. Tegyük fel, hogy a cél a négyjegyű 1234üzenet továbbítása kétdimenziós paritás séma segítségével. Először az üzenet számjegyei téglalap alakban vannak elrendezve:

12
34

A paritás számjegyeit azután kiszámítják, hogy az oszlopokat és a sorokat külön-külön összeadják:

12 3
34 7
46 

A 12334746 nyolc számjegyű sorozat az az üzenet, amelyet ténylegesen továbbítanak. Ha bármilyen hiba történik az átvitel során, akkor ez a hiba nem csak felismerhető, hanem kijavítható is. Tegyük fel, hogy a kapott üzenet hibát tartalmazott az elsõ számjegynél. A vevő átrendezi az üzenetet a rácsba:

9 2 3
34 7
46

A vevő láthatja, hogy az első sor és az első oszlop helytelenül is összeadódik. Ezen tudás és annak feltételezése alapján, hogy csak egy hiba történt, a vevő kijavíthatja a hibát. Két hiba kezelése érdekében négydimenziós sémára lenne szükség, több paritás számjegy árán. Többdimenziós paritásellenőrző kód.

EA 8 - Veszteséges és veszteség mentes tömörítés

Veszteséges

Vagy elhagyjuk a dekódolásnál nem fontos részeit a forrásfájlnak, pl zene esetében nem hallhtó frekvenciákat, képeknél pixeleket összevonhatunk.

• fraktál tömörítések
• hullám tömörítések

Veszteségmentes

• aritmetikai kódolások: valamilyen valósínűségen alapuló kódolások, ezek tömörítenek a leg veszteségmentesebben.
• lexikális kódolás:
  • LZW
  • LZ77/LZ78
  • DEFLATE
• futamhossz kódolás: bináris kódokhoz, veszteségmentes tömörítés a veszteséges tömörítés között

célja: tárolóhely igény csökkentése, akár belterjesen, a saját gépet tekintve is, adatátvitel idejének csökkentése

a lehetőséget az adja, hogy a legtöbb fájl redundáns.

Fogalmak: M->Kódoló->C(M)->Dekódoló->M'

• kódoló: az M egy tömörített C(M) reprezentációja állítja elő, amely remélhetően kevesebb bitet használ.

• kompresszió hányados: 0<C(M) bitjeinek a száma/M bitjeinek a sázma<=1. Csak akkor veszteségmentes ha a dekódoló pontosan az M üzenetet állítja elő.

• veszteségmentes tömörítésnél tipikusan 10%

• preliniáris(?) adatelemzés szükséges

• adaptív tömörítés

Dinamikus modell: a szövegen alapuló modellt generáll, sttisztikán alapul, pl Huffman

Adaptív modell: progresszíven tanulja és módosítja a modellt a szöveg olvasásával párhuzamosan., pl LZW

Futamhossz tömörítés: Ez egy egyszerű technika, az ismétlődő karakteek hosszú futamait használja fel.

LZV Nagy hátrány, hogy a szótárat is át kell küldeni!

• menet közben építi a szótárat

támadások:

• passzív támadás: ha a támadó csak leolvassa a üzenetet
• aktív támadás ha a támadó változtat az üzeneten

EA 9 zh felkészülés

• haming távolság
• lineáris kód
• tömörítés

konzultáció hétfőn 18-19:30