更新题解列表

Contents/00.Introduction/04.Solutions-List.md

@@ -1,4 +1,4 @@
-# LeetCode 题解（已完成 837 道）
+# LeetCode 题解（已完成 841 道）
 
 | 题号 | 标题 | 题解 | 标签 | 难度 |
 | :------ | :------ | :------ | :------ | :------ |
@@ -557,6 +557,7 @@
 | 1319 | [连通网络的操作次数](https://leetcode.cn/problems/number-of-operations-to-make-network-connected/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1319.%20%E8%BF%9E%E9%80%9A%E7%BD%91%E7%BB%9C%E7%9A%84%E6%93%8D%E4%BD%9C%E6%AC%A1%E6%95%B0.md) | 深度优先搜索、广度优先搜索、并查集、图 | 中等 |
 | 1338 | [数组大小减半](https://leetcode.cn/problems/reduce-array-size-to-the-half/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1338.%20%E6%95%B0%E7%BB%84%E5%A4%A7%E5%B0%8F%E5%87%8F%E5%8D%8A.md) | 贪心、数组、哈希表、排序、堆（优先队列） | 中等 |
 | 1343 | [大小为 K 且平均值大于等于阈值的子数组数目](https://leetcode.cn/problems/number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1343.%20%E5%A4%A7%E5%B0%8F%E4%B8%BA%20K%20%E4%B8%94%E5%B9%B3%E5%9D%87%E5%80%BC%E5%A4%A7%E4%BA%8E%E7%AD%89%E4%BA%8E%E9%98%88%E5%80%BC%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84%E6%95%B0%E7%9B%AE.md) | 数组、滑动窗口 | 中等 |
+| 1344 | [时钟指针的夹角](https://leetcode.cn/problems/angle-between-hands-of-a-clock/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1344.%20%E6%97%B6%E9%92%9F%E6%8C%87%E9%92%88%E7%9A%84%E5%A4%B9%E8%A7%92.md) | 数学 | 中等 |
 | 1349 | [参加考试的最大学生数](https://leetcode.cn/problems/maximum-students-taking-exam/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1349.%20%E5%8F%82%E5%8A%A0%E8%80%83%E8%AF%95%E7%9A%84%E6%9C%80%E5%A4%A7%E5%AD%A6%E7%94%9F%E6%95%B0.md) | 位运算、数组、动态规划、状态压缩、矩阵 | 困难 |
 | 1358 | [包含所有三种字符的子字符串数目](https://leetcode.cn/problems/number-of-substrings-containing-all-three-characters/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1358.%20%E5%8C%85%E5%90%AB%E6%89%80%E6%9C%89%E4%B8%89%E7%A7%8D%E5%AD%97%E7%AC%A6%E7%9A%84%E5%AD%90%E5%AD%97%E7%AC%A6%E4%B8%B2%E6%95%B0%E7%9B%AE.md) | 哈希表、字符串、滑动窗口 | 中等 |
 | 1381 | [设计一个支持增量操作的栈](https://leetcode.cn/problems/design-a-stack-with-increment-operation/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1381.%20%E8%AE%BE%E8%AE%A1%E4%B8%80%E4%B8%AA%E6%94%AF%E6%8C%81%E5%A2%9E%E9%87%8F%E6%93%8D%E4%BD%9C%E7%9A%84%E6%A0%88.md) | 栈、设计、数组 | 中等 |
@@ -585,10 +586,12 @@
 | 1556 | [千位分隔数](https://leetcode.cn/problems/thousand-separator/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1556.%20%E5%8D%83%E4%BD%8D%E5%88%86%E9%9A%94%E6%95%B0.md) | 字符串 | 简单 |
 | 1561 | [你可以获得的最大硬币数目](https://leetcode.cn/problems/maximum-number-of-coins-you-can-get/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1561.%20%E4%BD%A0%E5%8F%AF%E4%BB%A5%E8%8E%B7%E5%BE%97%E7%9A%84%E6%9C%80%E5%A4%A7%E7%A1%AC%E5%B8%81%E6%95%B0%E7%9B%AE.md) | 贪心、数组、数学、博弈、排序 | 中等 |
 | 1567 | [乘积为正数的最长子数组长度](https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1567.%20%E4%B9%98%E7%A7%AF%E4%B8%BA%E6%AD%A3%E6%95%B0%E7%9A%84%E6%9C%80%E9%95%BF%E5%AD%90%E6%95%B0%E7%BB%84%E9%95%BF%E5%BA%A6.md) | 贪心、数组、动态规划 | 中等 |
+| 1582 | [二进制矩阵中的特殊位置](https://leetcode.cn/problems/special-positions-in-a-binary-matrix/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1582.%20%E4%BA%8C%E8%BF%9B%E5%88%B6%E7%9F%A9%E9%98%B5%E4%B8%AD%E7%9A%84%E7%89%B9%E6%AE%8A%E4%BD%8D%E7%BD%AE.md) | 数组、矩阵 | 简单 |
 | 1593 | [拆分字符串使唯一子字符串的数目最大](https://leetcode.cn/problems/split-a-string-into-the-max-number-of-unique-substrings/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1593.%20%E6%8B%86%E5%88%86%E5%AD%97%E7%AC%A6%E4%B8%B2%E4%BD%BF%E5%94%AF%E4%B8%80%E5%AD%90%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E6%95%B0%E7%9B%AE%E6%9C%80%E5%A4%A7.md) | 哈希表、字符串、回溯 | 中等 |
 | 1595 | [连通两组点的最小成本](https://leetcode.cn/problems/minimum-cost-to-connect-two-groups-of-points/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1595.%20%E8%BF%9E%E9%80%9A%E4%B8%A4%E7%BB%84%E7%82%B9%E7%9A%84%E6%9C%80%E5%B0%8F%E6%88%90%E6%9C%AC.md) | 位运算、数组、动态规划、状态压缩、矩阵 | 困难 |
 | 1603 | [设计停车系统](https://leetcode.cn/problems/design-parking-system/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1603.%20%E8%AE%BE%E8%AE%A1%E5%81%9C%E8%BD%A6%E7%B3%BB%E7%BB%9F.md) | 设计、计数、模拟 | 简单 |
 | 1605 | [给定行和列的和求可行矩阵](https://leetcode.cn/problems/find-valid-matrix-given-row-and-column-sums/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1605.%20%E7%BB%99%E5%AE%9A%E8%A1%8C%E5%92%8C%E5%88%97%E7%9A%84%E5%92%8C%E6%B1%82%E5%8F%AF%E8%A1%8C%E7%9F%A9%E9%98%B5.md) | 贪心、数组、矩阵 | 中等 |
+| 1614 | [括号的最大嵌套深度](https://leetcode.cn/problems/maximum-nesting-depth-of-the-parentheses/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1614.%20%E6%8B%AC%E5%8F%B7%E7%9A%84%E6%9C%80%E5%A4%A7%E5%B5%8C%E5%A5%97%E6%B7%B1%E5%BA%A6.md) | 栈、字符串 | 简单 |
 | 1617 | [统计子树中城市之间最大距离](https://leetcode.cn/problems/count-subtrees-with-max-distance-between-cities/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1617.%20%E7%BB%9F%E8%AE%A1%E5%AD%90%E6%A0%91%E4%B8%AD%E5%9F%8E%E5%B8%82%E4%B9%8B%E9%97%B4%E6%9C%80%E5%A4%A7%E8%B7%9D%E7%A6%BB.md) | 位运算、树、动态规划、状态压缩、枚举 | 困难 |
 | 1631 | [最小体力消耗路径](https://leetcode.cn/problems/path-with-minimum-effort/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1631.%20%E6%9C%80%E5%B0%8F%E4%BD%93%E5%8A%9B%E6%B6%88%E8%80%97%E8%B7%AF%E5%BE%84.md) | 深度优先搜索、广度优先搜索、并查集、数组、二分查找、矩阵、堆（优先队列） | 中等 |
 | 1646 | [获取生成数组中的最大值](https://leetcode.cn/problems/get-maximum-in-generated-array/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1646.%20%E8%8E%B7%E5%8F%96%E7%94%9F%E6%88%90%E6%95%B0%E7%BB%84%E4%B8%AD%E7%9A%84%E6%9C%80%E5%A4%A7%E5%80%BC.md) | 数组、动态规划、模拟 | 简单 |
@@ -619,6 +622,7 @@
 | 1903 | [字符串中的最大奇数](https://leetcode.cn/problems/largest-odd-number-in-string/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1903.%20%E5%AD%97%E7%AC%A6%E4%B8%B2%E4%B8%AD%E7%9A%84%E6%9C%80%E5%A4%A7%E5%A5%87%E6%95%B0.md) | 贪心、数学、字符串 | 简单 |
 | 1925 | [统计平方和三元组的数目](https://leetcode.cn/problems/count-square-sum-triples/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1925.%20%E7%BB%9F%E8%AE%A1%E5%B9%B3%E6%96%B9%E5%92%8C%E4%B8%89%E5%85%83%E7%BB%84%E7%9A%84%E6%95%B0%E7%9B%AE.md) | 数学、枚举 | 简单 |
 | 1929 | [数组串联](https://leetcode.cn/problems/concatenation-of-array/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1929.%20%E6%95%B0%E7%BB%84%E4%B8%B2%E8%81%94.md) | 数组 | 简单 |
+| 1936 | [新增的最少台阶数](https://leetcode.cn/problems/add-minimum-number-of-rungs/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1936.%20%E6%96%B0%E5%A2%9E%E7%9A%84%E6%9C%80%E5%B0%91%E5%8F%B0%E9%98%B6%E6%95%B0.md) | 贪心、数组 | 中等 |
 | 1941 | [检查是否所有字符出现次数相同](https://leetcode.cn/problems/check-if-all-characters-have-equal-number-of-occurrences/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1941.%20%E6%A3%80%E6%9F%A5%E6%98%AF%E5%90%A6%E6%89%80%E6%9C%89%E5%AD%97%E7%AC%A6%E5%87%BA%E7%8E%B0%E6%AC%A1%E6%95%B0%E7%9B%B8%E5%90%8C.md) | 哈希表、字符串、计数 | 简单 |
 | 1947 | [最大兼容性评分和](https://leetcode.cn/problems/maximum-compatibility-score-sum/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1947.%20%E6%9C%80%E5%A4%A7%E5%85%BC%E5%AE%B9%E6%80%A7%E8%AF%84%E5%88%86%E5%92%8C.md) | 位运算、数组、动态规划、回溯、状态压缩 | 中等 |
 | 1984 | [学生分数的最小差值](https://leetcode.cn/problems/minimum-difference-between-highest-and-lowest-of-k-scores/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1984.%20%E5%AD%A6%E7%94%9F%E5%88%86%E6%95%B0%E7%9A%84%E6%9C%80%E5%B0%8F%E5%B7%AE%E5%80%BC.md) | 数组、排序、滑动窗口 | 简单 |

README.md

@@ -255,4 +255,4 @@
   - [动态规划优化题目](./Contents/10.Dynamic-Programming/11.DP-Optimization/04.DP-Optimization-List.md)
 
 ## 11. 附加内容
-## [12. LeetCode 题解（已完成 837 道）](./Contents/00.Introduction/04.Solutions-List.md)
+## [12. LeetCode 题解（已完成 841 道）](./Contents/00.Introduction/04.Solutions-List.md)

Solutions/1344. 时钟指针的夹角.md

@@ -0,0 +1,66 @@
+# [1344. 时钟指针的夹角](https://leetcode.cn/problems/angle-between-hands-of-a-clock/)
+
+- 标签：数学
+- 难度：中等
+
+## 题目链接
+
+- [1344. 时钟指针的夹角 - 力扣](https://leetcode.cn/problems/angle-between-hands-of-a-clock/)
+
+## 题目大意
+
+**描述**：给定两个数 $hour$ 和 $minutes$。
+
+**要求**：请你返回在时钟上，由给定时间的时针和分针组成的较小角的角度（$60$ 单位制）。
+
+**说明**：
+
+- $1 \le hour \le 12$。
+- $0 \le minutes \le 59$。
+- 与标准答案误差在 $10^{-5}$ 以内的结果都被视为正确结果。
+
+**示例**：
+
+- 示例 1：
+
+![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2020/02/08/sample_1_1673.png)
+
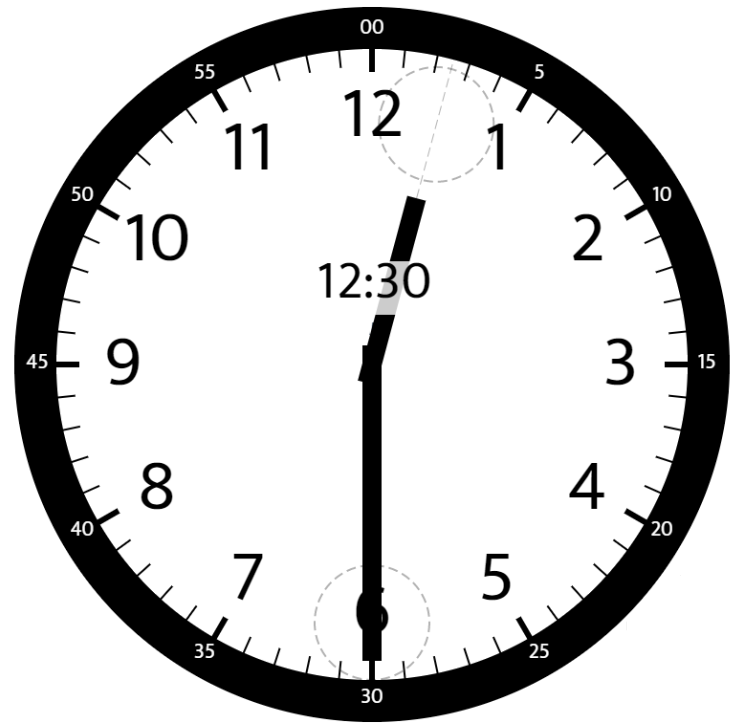+```python
+输入：hour = 12, minutes = 30
+输出：165
+```
+
+- 示例 2：
+
+![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2020/02/08/sample_2_1673.png)
+
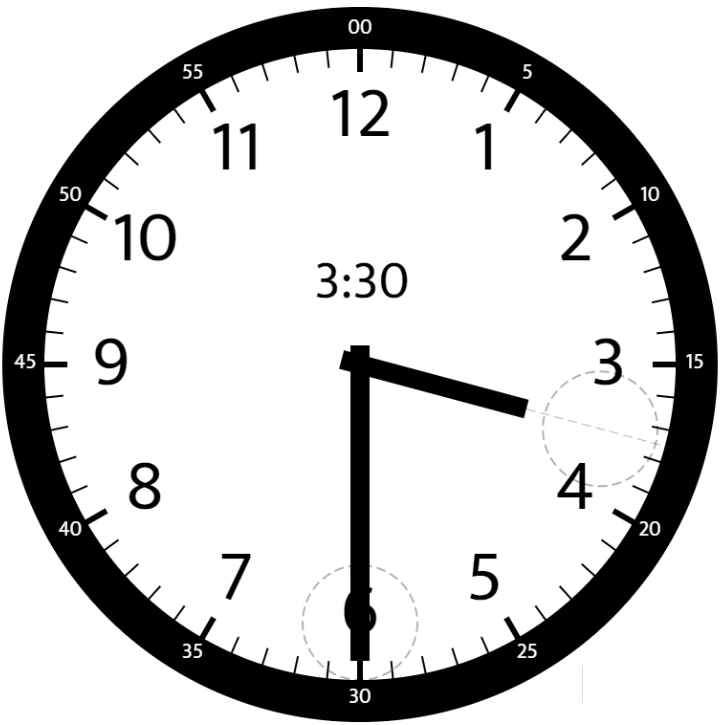+```python
+输入：hour = 3, minutes = 30
+输出；75
+```
+
+## 解题思路
+
+### 思路 1：数学
+
+1. 我们以 $00:00$ 为基准，分别计算出分针与 $00:00$ 中垂线的夹角，以及时针与 $00:00$ 中垂线的夹角。
+2. 然后计算出两者差值的绝对值 $diff$。当前差值可能为较小的角（小于 $180°$ 的角），也可能为较大的角（大于等于 $180°$ 的角）。
+3. 将差值的绝对值 $diff$ 与 $360 - diff$ 进行比较，取较小值作为答案。
+
+### 思路 1：代码
+
+```Python
+class Solution:
+    def angleClock(self, hour: int, minutes: int) -> float:
+        mins_angle = 6 * minutes
+        hours_angle = (hour % 12 + minutes / 60) * 30
+
+        diff = abs(hours_angle - mins_angle)
+        return min(diff, 360 - diff)
+```
+
+### 思路 1：复杂度分析
+
+- **时间复杂度**：$O(1)$。
+- **空间复杂度**：$O(1)$。
+

Solutions/1582. 二进制矩阵中的特殊位置.md

@@ -0,0 +1,83 @@
+# [1582. 二进制矩阵中的特殊位置](https://leetcode.cn/problems/special-positions-in-a-binary-matrix/)
+
+- 标签：数组、矩阵
+- 难度：简单
+
+## 题目链接
+
+- [1582. 二进制矩阵中的特殊位置 - 力扣](https://leetcode.cn/problems/special-positions-in-a-binary-matrix/)
+
+## 题目大意
+
+**描述**：给定一个 $m \times n$ 的二进制矩阵 $mat$。
+
+**要求**：返回矩阵 $mat$ 中特殊位置的数量。
+
+**说明**：
+
+- **特殊位置**：如果位置 $(i, j)$ 满足 $mat[i][j] == 1$ 并且行 $i$ 与列 $j$ 中的所有其他元素都是 $0$（行和列的下标从 $0$ 开始计数），那么它被称为特殊位置。
+- $m == mat.length$。
+- $n == mat[i].length$。
+- $1 \le m, n \le 100$。
+- $mat[i][j]$ 是 $0$ 或 $1$。
+
+**示例**：
+
+- 示例 1：
+
+![](https://assets.leetcode.com/uploads/2021/12/23/special1.jpg)
+
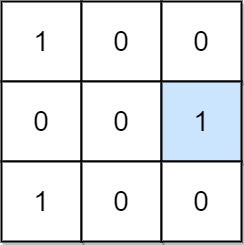+```python
+输入：mat = [[1,0,0],[0,0,1],[1,0,0]]
+输出：1
+解释：位置 (1, 2) 是一个特殊位置，因为 mat[1][2] == 1 且第 1 行和第 2 列的其他所有元素都是 0。
+```
+
+- 示例 2：
+
+![img](https://assets.leetcode.com/uploads/2021/12/24/special-grid.jpg)
+
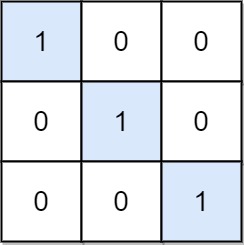+```python
+输入：mat = [[1,0,0],[0,1,0],[0,0,1]]
+输出：3
+解释：位置 (0, 0)，(1, 1) 和 (2, 2) 都是特殊位置。
+```
+
+## 解题思路
+
+### 思路 1：模拟
+
+1. 按照行、列遍历二位数组 $mat$。
+2. 使用数组 $row\underline{}cnts$、$col\underline{}cnts$ 分别记录每行和每列所含 $1$ 的个数。
+3. 再次按照行、列遍历二维数组 $mat$。
+4. 统计满足 $mat[row][col] == 1$ 并且 $row\underline{}cnts[row] == col\underline{}cnts[col] == 1$ 的位置个数。 
+5. 返回答案。
+
+### 思路 1：代码
+
+```Python
+class Solution:
+    def numSpecial(self, mat: List[List[int]]) -> int:
+        rows, cols = len(mat), len(mat[0])
+        row_cnts = [0 for _ in range(rows)]
+        col_cnts = [0 for _ in range(cols)]
+
+        for row in range(rows):
+            for col in range(cols):
+                row_cnts[row] += mat[row][col]
+                col_cnts[col] += mat[row][col]
+
+        ans = 0
+        for row in range(rows):
+            for col in range(cols):
+                if mat[row][col] == 1 and row_cnts[row] == 1 and col_cnts[col] == 1:
+                    ans += 1
+
+        return ans
+```
+
+### 思路 1：复杂度分析
+
+- **时间复杂度**：$O(m \times n)$，其中 $m$、$n$ 分别为数组 $mat$ 的行数和列数。
+- **空间复杂度**：$O(m + n)$。
+

Solutions/1614. 括号的最大嵌套深度.md

@@ -0,0 +1,83 @@
+# [1614. 括号的最大嵌套深度](https://leetcode.cn/problems/maximum-nesting-depth-of-the-parentheses/)
+
+- 标签：栈、字符串
+- 难度：简单
+
+## 题目链接
+
+- [1614. 括号的最大嵌套深度 - 力扣](https://leetcode.cn/problems/maximum-nesting-depth-of-the-parentheses/)
+
+## 题目大意
+
+**描述**：给你一个有效括号字符串 $s$。
+
+**要求**：返回该字符串 $s$ 的嵌套深度 。
+
+**说明**：
+
+- 如果字符串满足以下条件之一，则可以称之为 有效括号字符串（valid parentheses string，可以简写为 VPS）：
+  - 字符串是一个空字符串 `""`，或者是一个不为 `"("` 或 `")"` 的单字符。
+  - 字符串可以写为 $AB$（$A$ 与 B 字符串连接），其中 $A$ 和 $B$ 都是有效括号字符串 。
+  - 字符串可以写为 ($A$)，其中 $A$ 是一个有效括号字符串。
+
+- 类似地，可以定义任何有效括号字符串 $s$ 的 嵌套深度 $depth(s)$：
+
+  - `depth("") = 0`。
+  - `depth(C) = 0`，其中 $C$ 是单个字符的字符串，且该字符不是 `"("` 或者 `")"`。
+  - `depth(A + B) = max(depth(A), depth(B))`，其中 $A$ 和 $B$ 都是 有效括号字符串。
+  - `depth("(" + A + ")") = 1 + depth(A)`，其中 A 是一个 有效括号字符串。
+- $1 \le s.length \le 100$。
+- $s$ 由数字 $0 \sim 9$ 和字符 `'+'`、`'-'`、`'*'`、`'/'`、`'('`、`')'` 组成。
+- 题目数据保证括号表达式 $s$ 是有效的括号表达式。
+
+**示例**：
+
+- 示例 1：
+
+```python
+输入：s = "(1+(2*3)+((8)/4))+1"
+输出：3
+解释：数字 8 在嵌套的 3 层括号中。
+```
+
+- 示例 2：
+
+```python
+输入：s = "(1)+((2))+(((3)))"
+输出：3
+```
+
+## 解题思路
+
+### 思路 1：模拟
+
+我们可以使用栈来进行模拟括号匹配。遍历字符串 $s$，如果遇到左括号，则将其入栈，如果遇到右括号，则弹出栈中的左括号，与当前右括号进行匹配。在整个过程中栈的大小的最大值，就是我们要求的 $s$ 的嵌套深度，其实也是求最大的连续左括号的数量（跳过普通字符，并且与右括号匹配后）。具体步骤如下：
+
+1. 使用 $ans$ 记录最大的连续左括号数量，使用 $cnt$ 记录当前栈中左括号的数量。
+2. 遍历字符串 $s$：
+   1. 如果遇到左括号，则令 $cnt$ 加 $1$。
+   2. 如果遇到右括号，则令 $cnt$ 减 $1$。
+   3. 将 $cnt$ 与答案进行比较，更新最大的连续左括号数量。
+3. 遍历完字符串 $s$，返回答案 $ans$。
+
+### 思路 1：代码
+
+```Python
+class Solution:
+    def maxDepth(self, s: str) -> int:
+        ans, cnt = 0, 0
+        for ch in s:
+            if ch == '(':
+                cnt += 1
+            elif ch == ')':
+                cnt -= 1
+            ans = max(ans, cnt)
+
+        return ans
+```
+
+### 思路 1：复杂度分析
+
+- **时间复杂度**：$O(n)$，其中 $n$ 为字符串 $s$ 的长度。
+- **空间复杂度**：$O(1)$。
+

Solutions/1936. 新增的最少台阶数.md

@@ -0,0 +1,73 @@
+# [1936. 新增的最少台阶数](https://leetcode.cn/problems/add-minimum-number-of-rungs/)
+
+- 标签：贪心、数组
+- 难度：中等
+
+## 题目链接
+
+- [1936. 新增的最少台阶数 - 力扣](https://leetcode.cn/problems/add-minimum-number-of-rungs/)
+
+## 题目大意
+
+**描述**：给定一个严格递增的整数数组 $rungs$，用于表示梯子上每一台阶的高度。当前你正站在高度为 $0$ 的地板上，并打算爬到最后一个台阶。
+
+另给定一个整数 $dist$。每次移动中，你可以到达下一个距离当前位置（地板或台阶）不超过 $dist$ 高度的台阶。当前，你也可以在任何正整数高度插入尚不存在的新台阶。
+
+**要求**：返回爬到最后一阶时必须添加到梯子上的最少台阶数。
+
+**说明**：
+
+- 
+
+**示例**：
+
+- 示例 1：
+
+```python
+输入：rungs = [1,3,5,10], dist = 2
+输出：2
+解释：
+现在无法到达最后一阶。
+在高度为 7 和 8 的位置增设新的台阶，以爬上梯子。 
+梯子在高度为 [1,3,5,7,8,10] 的位置上有台阶。
+```
+
+- 示例 2：
+
+```python
+输入：rungs = [3,4,6,7], dist = 2
+输出：1
+解释：
+现在无法从地板到达梯子的第一阶。 
+在高度为 1 的位置增设新的台阶，以爬上梯子。 
+梯子在高度为 [1,3,4,6,7] 的位置上有台阶。
+```
+
+## 解题思路
+
+### 思路 1：贪心算法 + 模拟
+
+1. 遍历梯子的每一层台阶。
+2. 计算每一层台阶与上一层台阶之间的差值 $diff$。
+3. 每层最少需要新增的台阶数为 $\lfloor \frac{diff - 1}{dist} \rfloor$，将其计入答案 $ans$ 中。
+4. 遍历完返回答案。
+
+### 思路 1：代码
+
+```Python
+class Solution:
+    def addRungs(self, rungs: List[int], dist: int) -> int:
+        ans, cur = 0, 0
+        for h in rungs:
+            diff = h - cur
+            ans += (diff - 1) // dist
+            cur = h
+
+        return ans
+```
+
+### 思路 1：复杂度分析
+
+- **时间复杂度**：$O(n)$，其中 $n$ 为数组 $rungs$ 的长度。
+- **空间复杂度**：$O(1)$。
+