Prims Algorithm Tutorial

tutorials/graph-theory/prims-algorithm.md

@@ -1,12 +1,382 @@
 ---
 title: "Prim's Algorithm"
-description: 'Coming Soon!'
+description: "Prim's algorithm finds the Minimum Spanning Tree (MST) of a graph, ensuring all vertices are connected with the smallest possible total edge weight in O(E + V log V) time."
 draft: true
 keywords:
   - leetcode
   - tutorial
   - prim
   - algorithm
 ---
+<TutorialAuthors names="@Infonioknight"/>
 
-Coming Soon
+## Suggested Pre-requisites
+Before moving on to learn the Prims algorithm, it is suggested that you know what a [Minimum Spanning Tree (MST)](../graph-theory/minimum-spanning-tree.md) is.
+
+## Overview
+The Prims algorithm is a [Greedy Algorithm](../basic-topics/greedy.md)  used to find a minimum spanning tree (MST) for a connected weighted undirected graph. In simpler terms, it finds a subset of the edges that forms a tree that includes *every* vertex, where the total **weight** of all the **edges** in the tree is **minimized**.
+
+### How does it work? 
+- It starts with a single vertex (that can be randomly chosen) and gradually expands the tree by adding the smallest edge that connects a vertex present in the tree to a vertex not yet in the tree.
+- It continues until every vertex is included in the tree.
+- The algorithm uses a priority queue or similar structure to efficiently track the smallest edge that can be added to the tree at each step.
+
+**Note:** Since the starting vertex is chosen at random, it is possible to have different edges included in the MST for the same graph, but the total edge weight of the MST will still have the same minimum value.
+
+### Complexity and Use-Cases
+- When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O((E + V)log V)$ (when implemented using a binary heap), where $E$ is the number of edges and $V$ is the number of vertices.  
+- To calculate the time complexity, we know that each extraction operation from a priority queue takes $O(log V)$ time. The algorithm extracts a vertex from this queue a total of $V$ times (traverse the entire graph), and for each edge, the algorithm will have to update the priority of an adjacent vertex. This takes place a total of $E$ times. Combining these two (extraction + updation), processes on the queue take place a total of $(E + V)$ times.  
+- This brings us to the final time complexity of $O((E + V)log V)$. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better. This is because of the presence of $O(ElogV)$ term in the time complexity, which doesn't increase the computation time of a priority queue operation $O(log V)$. This is unlike that of Kruskal's where the edges are sorted, which takes $O(Elog E)$ time.
+
+The space complexity of the Prims Algorithm is $O(V + E)$, where $V$ is the number of vertices and $E$ is the number of edges.
+
+Prim's algorithm is widely used in network design, where the goal is to minimize the cost of building a network while connecting all nodes. Examples include laying cables, designing road networks, or creating efficient communication paths. It is also used as a building block in other algorithms for solving more complex problems.
+
+![Prims Algorithm Image](https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg)  
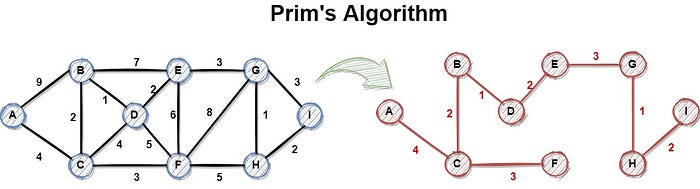+_Source: https://plainenglish.io/blog/an-introduction-to-prims-algorithm-in-python-8c764df5936f_
+
+## Example 1: [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree)
+**Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link.
+
+### Example 
+**Input:** $N = 3$, $connections = [[1,2,5],[1,3,6],[2,3,1]]$
+
+First, for clarity we make a note of the connections in a way that's easy to understand.
+
+- $city 1$ and $city 2$ are connected by a path of cost $5$
+- $city 1$ and $city 3$ are connected by a path of cost $6$
+- $city 2$ and $city 3$ are connected by a path of cost $1$
+
+Our goal is to find the minimum so that for every pair of cities, there exists a path of connections that connects these two cities together. If that is possible, we return the $cost$. If it's impossible, we return $-1$
+
+Assuming we start at $city 1$, we first pick the smallest connection from here - Namely the one to $city 2$ with a cost of 5
+
+Current total cost = $0 + 5 = 5$
+
+Now we have two remaining connections to consider from our connected cities:
+    - Connect $city 2$ to $city 3$ (cost $1$)
+    - Connect $city 1$ to $city 3$ (cost $6$)
+
+Clearly the **cheapest** one is the one with cost $1$.
+So, the total cost is $5 + 1 = 6$
+
+Now all the cities have been connected. So we return our **solution** $6$.
+
+### Approach
+First, we convert the given 'connections' array, into an adjacency list for ease of traversing.
+<Tabs>
+
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+connections = [[1,2,5],[1,3,6],[2,3,1]] # Example
+adjacency_list = {}
+
+for connection in connections:
+  if connection[0] not in adjacency_list:
+    adjacency_list[connection[0]] = []
+  if connection[1] not in adjacency_list:
+    adjacency_list[connection[1]] = []
+  adjacency_list[connection[0]].append((connection[2], connection[1]))
+  adjacency_list[connection[1]].append((connection[2], connection[0]))
+```
+</TabItem>
+</Tabs>
+
+The adjacency list will look like:
+```
+1: [(5, 2), (6, 3)]
+2: [(5, 1), (1, 3)]
+3: [(6, 1), (1, 2)]
+```
+Where each tuple consists of $(cost, destination)$.
+
+Now, to find the minimum cost, we use the below approach.
+### Explanation
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+for connection in adjacency_list[start]:
+  heapq.heappush(connection_queue, connection)
+```
+</TabItem>
+</Tabs>
+
+First, we push all the connections of the starting node into the priority queue. On doing so, the nodes with edges of MINIMUM COST come in front.
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+while len(seen) < n and connection_queue:
+  cost, current = heapq.heappop(connection_queue)
+  if current in seen:
+    continue
+
+  res += cost
+  seen.add(current)
+```
+</TabItem>
+</Tabs>
+
+- Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost). We also ensure that the node selected hasn't already been visited.
+- If the node hasn't been visited, we then add the cost to our solution and mark the node as visited.
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+    for connection in adjacency_list[current]:
+      if connection[1] not in seen:
+        heapq.heappush(connection_queue, connection)
+
+if len(seen) < n: return -1
+else: return res
+```
+</TabItem>
+</Tabs>
+
+- After that, we check the adjacency list for all the nodes connected to the current node (the node visited most recently) and if the connections of this node haven't been visited, they are added to the priority queue.
+- This process goes on until one of two outcomes is achieved.
+    - **Not all** the nodes have been visited, in which case the number of nodes in 'seen' will be less than the total number of nodes. In this case, we do not have a successful output and return $-1$
+    - If all the nodes have been visited, we return the solution.
+
+#### Final Code
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+import random
+import heapq
+
+class Solution:
+  def connecting_cities_with_minimum_cost(self, adjacency_list):
+    # Number of nodes in the given tree
+    n = len(adjacency_list)
+    # A list we will use to implement a priority queue
+    connection_queue = []
+    # Total minimum cost to traverse all the cities
+    res = 0
+    # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+    start = random.randint(1, n)
+    # To ensure we don't create closed loops
+    seen = set([start])
+
+    for connection in adjacency_list[start]:
+      heapq.heappush(connection_queue, connection)
+
+    while len(seen) < n and connection_queue:
+      cost, current = heapq.heappop(connection_queue)
+      if current in seen:
+        continue
+
+      res += cost
+      seen.add(current)
+
+      for connection in adjacency_list[current]:
+        if connection[1] not in seen:
+          heapq.heappush(connection_queue, connection)
+
+    if len(seen) < n: return -1
+    return res
+
+
+  def minimumCost(self, n: int, connections: List[List[int]]) -> int:
+    adjacency_list = {}
+
+    for connection in connections:
+      if connection[0] not in adjacency_list:
+        adjacency_list[connection[0]] = []
+      if connection[1] not in adjacency_list:
+        adjacency_list[connection[1]] = []
+      adjacency_list[connection[0]].append((connection[2], connection[1]))
+      adjacency_list[connection[1]].append((connection[2], connection[0]))
+
+    return self.connecting_cities_with_minimum_cost(adjacency_list)
+```
+</TabItem>
+</Tabs>
+
+## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points)
+### Instructions 
+You are given an array $points$ representing integer coordinates of some points on a 2D-plane, where $points[i]$ = $[x_i, y_i]$.
+The cost of connecting two points $[x_i, y_i]$ and $[x_j, y_j]$ is the **Manhattan distance** between them: $|x_i - x_j|$ + $|y_i - y_j|$, where $|val|$ denotes the absolute value of $val$.
+
+Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
+
+
+### Approach
+- This problem is also, extremely similar to the previous one. Only difference being the way the input is provided here (as a list of points, where you calculate the weight of the edges)
+- The approach I would suggest, would be to assume this as a **Complete Tree** (Every node is connected to every other node). So the way to convert the given points, into an adjacency list would be as below.
+
+<Tabs>
+
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
+
+adjacency_list = {}
+n = len(points)
+for i in range(n):
+  current = tuple(points[i])
+  for j in range(i + 1, n):
+    destination = tuple(points[j])
+      if current not in adjacency_list:
+        adjacency_list[current] = []
+      if destination not in adjacency_list:
+        adjacency_list[destination] = []
+
+      # The formula in the second item of the append, is to calculate the Manhattan Distance between two points (the edge weight)
+      adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+      adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+```
+</TabItem>
+</Tabs>
+
+The adjacency list, will look something like this:
+```
+(0, 0): [[4, (2, 2)], [13, (3, 10)], [7, (5, 2)], [7, (7, 0)]]
+(2, 2): [[4, (0, 0)], [9, (3, 10)], [3, (5, 2)], [7, (7, 0)]]
+(3, 10): [[13, (0, 0)], [9, (2, 2)], [10, (5, 2)], [14, (7, 0)]]
+(5, 2): [[7, (0, 0)], [3, (2, 2)], [10, (3, 10)], [4, (7, 0)]]
+(7, 0): [[7, (0, 0)], [7, (2, 2)], [14, (3, 10)], [4, (5, 2)]]
+```
+
+The rest of the code follows an almost identical pattern as the previous one. The below being probably the only changes regarding to how the entire traversal is started.
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+# Here, our helper function contains one additional argument - the initial point (as here we don't need to randomly start)
+def min_cost_points(adjacency_list, initial):
+  # Number of nodes in the given tree
+  n = len(adjacency_list)
+  # A list we will use to implement a priority queue
+  connection_queue = []
+  # Total minimum cost to connect all points
+  res = 0
+  start = tuple(initial)
+  # To ensure we don't create closed loops
+  seen = set([start])
+```
+
+</TabItem>
+</Tabs>
+
+Below, is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution)
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+    for connection in adjacency_list[start]:
+      heapq.heappush(connection_queue, connection)
+
+    while len(seen) < n and connection_queue:
+      cost, current = heapq.heappop(connection_queue)
+      if current in seen:
+        continue
+
+      res += cost
+      seen.add(current)
+
+      for connection in adjacency_list[current]:
+        if connection[1] not in seen:
+          heapq.heappush(connection_queue, connection)
+
+    return res
+```
+</TabItem>
+</Tabs>
+
+#### Final Code
+
+<Tabs>
+<TabItem value="py" label="Python">
+<SolutionAuthor name="@Infonioknight"/>
+
+```py
+import heapq
+
+class Solution:
+  def min_cost_points(self, adjacency_list, initial):
+    # Number of nodes in the given tree
+    n = len(adjacency_list)
+    # A list we will use to implement a priority queue
+    connection_queue = []
+    # Total minimum cost to connect all points
+    res = 0
+    # Taking the assumption that the n nodes in the adjacency list are from 1 to n
+    start = tuple(initial)
+    # To ensure we don't create closed loops
+    seen = set([start])
+
+    for connection in adjacency_list[start]:
+        heapq.heappush(connection_queue, connection)
+
+    while len(seen) < n and connection_queue:
+      cost, current = heapq.heappop(connection_queue)
+      if current in seen:
+        continue
+
+      res += cost
+      seen.add(current)
+
+      for connection in adjacency_list[current]:
+        if connection[1] not in seen:
+          heapq.heappush(connection_queue, connection)
+
+    return res
+
+  def minCostConnectPoints(self, points: List[List[int]]) -> int:
+    # Inititalizing an empty adjacency list to transform the points into something more convenient to work with
+    adjacency_list = {}
+    # Total number of items in the list of points (each coordinate pair is a point)
+    n = len(points)
+    for i in range(n):
+      current = tuple(points[i])
+      for j in range(i + 1, n):
+        destination = tuple(points[j])
+        if current not in adjacency_list:
+          adjacency_list[current] = []
+        if destination not in adjacency_list:
+          adjacency_list[destination] = []
+
+        adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination])
+        adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current])
+
+    if n < 2: return 0
+    return self.min_cost_points(adjacency_list, points[0])
+```
+</TabItem>
+</Tabs>
+
+export const suggestedProblems = [ 
+  { 
+    "problemName": "1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree", 
+    "difficulty": "Hard", 
+    "leetCodeLink": "https://leetcode.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/", 
+    "solutionLink": "" 
+  }, 
+  { 
+    "problemName": "0787 - Cheapest Flights Within K Stops", 
+    "difficulty": "Medium", 
+    "leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/", 
+    "solutionLink": "../../solutions/0700-0799/cheapest-flights-within-k-stops-medium" 
+  },
+]
+
+<Table title="Suggested Problems" data={suggestedProblems} />