-
-
Notifications
You must be signed in to change notification settings - Fork 220
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Prims Algorithm Tutorial #711
Open
Infonioknight
wants to merge
8
commits into
wingkwong:main
Choose a base branch
from
Infonioknight:patch-1
base: main
Could not load branches
Branch not found: {{ refName }}
Loading
Could not load tags
Nothing to show
Loading
Are you sure you want to change the base?
Some commits from the old base branch may be removed from the timeline,
and old review comments may become outdated.
+372
−2
Open
Changes from 5 commits
Commits
Show all changes
8 commits
Select commit
Hold shift + click to select a range
904a08a
Prims Algorithm Tutorial
Infonioknight 8545f87
Update prims-algorithm.md
Infonioknight 590a2a3
Update prims-algorithm.md
Infonioknight 68a45b2
Update prims-algorithm.md
Infonioknight a09a98c
Update prims-algorithm.md
Infonioknight 2d9bca1
Update prims-algorithm.md
Infonioknight 88e6f93
Update prims-algorithm.md
Infonioknight 44cc32c
Update prims-algorithm.md
Infonioknight File filter
Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -1,12 +1,370 @@ | ||
| --- | ||
| title: "Prim's Algorithm" | ||
| description: 'Coming Soon!' | ||
| description: "Prim's algorithm finds the Minimum Spanning Tree (MST) of a graph, ensuring all vertices are connected with the smallest possible total edge weight in O(E + V log V) time." | ||
| draft: true | ||
| keywords: | ||
| - leetcode | ||
| - tutorial | ||
| - prim | ||
| - algorithm | ||
| --- | ||
| <TutorialAuthors names="@Infonioknight"/> | ||
|
|
||
| Coming Soon | ||
| ## Suggested Pre-requisites | ||
| Before moving on to learn the Prims algorithm, it is suggested that you know what a [Minimum Spanning Tree (MST)](../graph-theory/minimum-spanning-tree.md) is. | ||
|
|
||
| ## Overview | ||
| The Prims algorithm is a [Greedy Algorithm](../basic-topics/greedy.md) used to find a minimum spanning tree (MST) for a connected weighted undirected graph. In simpler terms, it finds a subset of the edges that forms a tree that includes *every* vertex, where the total **weight** of all the **edges** in the tree is **minimized**. | ||
|
|
||
| ### How does it work? | ||
| - It starts with a single vertex (that can be randomly chosen) and gradually expands the tree by adding the smallest edge that connects a vertex present in the tree to a vertex not yet in the tree. | ||
| - It continues until every vertex is included in the tree. | ||
| - The algorithm uses a priority queue or similar structure to efficiently track the smallest edge that can be added to the tree at each step. | ||
|
|
||
| **Note:** Since the starting vertex is chosen at random, it is possible to have different edges included in the MST for the same graph, but the total edge weight of the MST will still have the same minimum value. | ||
|
|
||
| ### Complexity and Use-Cases | ||
| When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better. | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
|
|
||
| The space complexity of the Prims Algorithm is $O(V + E)$, where $V$ is the number of vertices and $E$ is the number of edges. | ||
|
|
||
| Prim's algorithm is widely used in network design, where the goal is to minimize the cost of building a network while connecting all nodes. Examples include laying cables, designing road networks, or creating efficient communication paths. It is also used as a building block in other algorithms for solving more complex problems. | ||
|
|
||
| 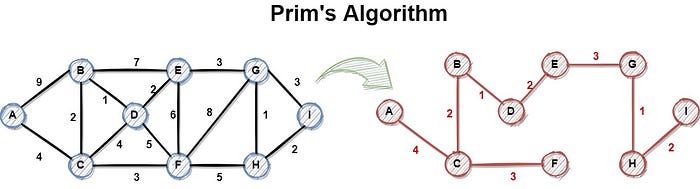 | ||
|
|
||
| _Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_ | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
|
|
||
| ## Example 1: [1135 - Connecting Cities With Minimum Cost](https://leetcode.com/problems/connecting-cities-with-minimum-cost/description/?envType=problem-list-v2&envId=minimum-spanning-tree) | ||
| **Note:** The above link requires the Leetcode Subscription. To view the problem, use [this](https://leetcode.ca/all/1135.html) alternate link. | ||
|
|
||
| ### Instructions: | ||
| - There are N cities numbered from 1 to N. | ||
| - You are given connections, where each `connections[i] = [city1, city2, cost]` represents the cost to connect `city1` and `city2 ` together. The connections are all bidirectional. | ||
| - Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return $-1$. | ||
|
|
||
| #### Example: | ||
|
|
||
| **Input:** N = `3`, connections = `[[1,2,5],[1,3,6],[2,3,1]]` | ||
|
|
||
| **Output:** `6` | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
|
|
||
| ### Approach | ||
| First, we convert the given 'connections' array, into an adjacency list for ease of traversing. | ||
| <Tabs> | ||
|
|
||
| <TabItem value="py1" label="Python"> | ||
wingkwong marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| connections = [[1,2,5],[1,3,6],[2,3,1]] # Example | ||
| adjacency_list = {} | ||
|
|
||
| for connection in connections: | ||
| if connection[0] not in adjacency_list: | ||
| adjacency_list[connection[0]] = [] | ||
| if connection[1] not in adjacency_list: | ||
| adjacency_list[connection[1]] = [] | ||
| adjacency_list[connection[0]].append((connection[2], connection[1])) | ||
| adjacency_list[connection[1]].append((connection[2], connection[0])) | ||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| The adjacency list will look like: | ||
| ``` | ||
| 1: [(5, 2), (6, 3)] | ||
| 2: [(5, 1), (1, 3)] | ||
| 3: [(6, 1), (1, 2)] | ||
| ``` | ||
| Where each tuple consists of '(cost, destination)'. | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
|
|
||
| Now, to find the minimum cost, we use the below approach. | ||
| ### Explanation: | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py2" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| for connection in adjacency_list[start]: | ||
| heapq.heappush(connection_queue, connection) | ||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| First, we push all the connections of the starting node into the priority queue. On doing so, the nodes with edges of MINIMUM COST come in front. | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py3" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| while len(seen) < n and connection_queue: | ||
| cost, current = heapq.heappop(connection_queue) | ||
| if current in seen: | ||
| continue | ||
|
|
||
| res += cost | ||
| seen.add(current) | ||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| - Then, we take the first element out of the queue (this is the node we ideally will add to our MST as it will have the minimum cost. We also ensure that the node selected hasn't already been visited. | ||
| - If the node hasn't been visited, we then add the cost to our solution and mark the node as visited. | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py4" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| for connection in adjacency_list[current]: | ||
| if connection[1] not in seen: | ||
| heapq.heappush(connection_queue, connection) | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
|
|
||
| if len(seen) < n: return -1 | ||
| else: return res | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| - After that, we check the adjacency list for all the nodes connected to the current node (the node visited most recently) and if the connections of this node haven't been visited, they are added to the priority queue. | ||
| - This process goes on until one of two outcomes is achieved. | ||
| - **Not all** the nodes have been visited, in which case the number of nodes in 'seen' will be less than the total number of nodes. In this case, we do not have a successful output and return $-1$ | ||
| - If all the nodes have been visited, we return the solution. | ||
|
|
||
| #### Final Code: | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py5" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| import random | ||
| import heapq | ||
|
|
||
| class Solution: | ||
| def connecting_cities_with_minimum_cost(self, adjacency_list): | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| # Number of nodes in the given tree | ||
| n = len(adjacency_list) | ||
| # A list we will use to implement a priority queue | ||
| connection_queue = [] | ||
| # Total minimum cost to traverse all the cities | ||
| res = 0 | ||
| # Taking the assumption that the n nodes in the adjacency list are from 1 to n | ||
| start = random.randint(1, n) | ||
| # To ensure we don't create closed loops | ||
| seen = set([start]) | ||
|
|
||
| for connection in adjacency_list[start]: | ||
| heapq.heappush(connection_queue, connection) | ||
|
|
||
| while len(seen) < n and connection_queue: | ||
| cost, current = heapq.heappop(connection_queue) | ||
| if current in seen: | ||
| continue | ||
|
|
||
| res += cost | ||
| seen.add(current) | ||
|
|
||
| for connection in adjacency_list[current]: | ||
| if connection[1] not in seen: | ||
| heapq.heappush(connection_queue, connection) | ||
|
|
||
| if len(seen) < n: return -1 | ||
| return res | ||
|
|
||
|
|
||
| def minimumCost(self, n: int, connections: List[List[int]]) -> int: | ||
| adjacency_list = {} | ||
|
|
||
| for connection in connections: | ||
| if connection[0] not in adjacency_list: | ||
| adjacency_list[connection[0]] = [] | ||
| if connection[1] not in adjacency_list: | ||
| adjacency_list[connection[1]] = [] | ||
| adjacency_list[connection[0]].append((connection[2], connection[1])) | ||
| adjacency_list[connection[1]].append((connection[2], connection[0])) | ||
|
|
||
| return self.connecting_cities_with_minimum_cost(adjacency_list) | ||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| ## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points) | ||
| ### Instructions: | ||
| You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i]` = `[xi, yi]`. | ||
| The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **Manhattan distance** between them: `|xi - xj|` + `|yi - yj|`, where `|val|` denotes the absolute value of `val`. | ||
|
|
||
| Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points. | ||
|
|
||
| #### Example: | ||
|
|
||
| **Input:** points = `[[0,0],[2,2],[3,10],[5,2],[7,0]]` | ||
|
|
||
| **Output:** `20` | ||
|
|
||
| ### Approach | ||
| - This problem is also, extremely similar to the previous one. Only difference being the way the input is provided here (as a list of points, where you calculate the weight of the edges) | ||
| - The approach I would suggest, would be to assume this as a **Complete Tree** (Every node is connected to every other node). So the way to convert the given points, into an adjacency list would be as below. | ||
|
|
||
| <Tabs> | ||
|
|
||
| <TabItem value="py6" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| points = [[0,0],[2,2],[3,10],[5,2],[7,0]] | ||
|
|
||
| adjacency_list = {} | ||
| for i in range(len(points)): | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| current = tuple(points[i]) | ||
| for j in range(i+1, len(points)): | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| destination = tuple(points[j]) | ||
| if current not in adjacency_list: | ||
| adjacency_list[current] = [] | ||
| if destination not in adjacency_list: | ||
| adjacency_list[destination] = [] | ||
|
|
||
| # The formula in the second item of the append, is to calculate the Manhattan Distance between two points (the edge weight) | ||
| adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination]) | ||
| adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current]) | ||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| The adjacency list, will look something like this: | ||
| ``` | ||
| (0, 0): [[4, (2, 2)], [13, (3, 10)], [7, (5, 2)], [7, (7, 0)]] | ||
| (2, 2): [[4, (0, 0)], [9, (3, 10)], [3, (5, 2)], [7, (7, 0)]] | ||
| (3, 10): [[13, (0, 0)], [9, (2, 2)], [10, (5, 2)], [14, (7, 0)]] | ||
| (5, 2): [[7, (0, 0)], [3, (2, 2)], [10, (3, 10)], [4, (7, 0)]] | ||
| (7, 0): [[7, (0, 0)], [7, (2, 2)], [14, (3, 10)], [4, (5, 2)]] | ||
| ``` | ||
|
|
||
| The rest of the code follows an almost identical pattern as the previous one. The below being probably the only changes regarding to how the entire traversal is started. | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py7" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| # Here, our helper function contains one additional argument - the initial point (as here we don't need to randomly start) | ||
| def min_cost_points(adjacency_list, initial): | ||
| # Number of nodes in the given tree | ||
| n = len(adjacency_list) | ||
| # A list we will use to implement a priority queue | ||
| connection_queue = [] | ||
| # Total minimum cost to connect all points | ||
| res = 0 | ||
| start = tuple(initial) | ||
| # To ensure we don't create closed loops | ||
| seen = set([start]) | ||
| ``` | ||
|
|
||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| The below is the implementation of the main function. It is identical to the previous example in every way except for the final output (as in this question, we are guaranteed a solution) | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py8" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| for connection in adjacency_list[start]: | ||
| heapq.heappush(connection_queue, connection) | ||
|
|
||
| while len(seen) < n and connection_queue: | ||
| cost, current = heapq.heappop(connection_queue) | ||
| if current in seen: | ||
| continue | ||
|
|
||
| res += cost | ||
| seen.add(current) | ||
|
|
||
| for connection in adjacency_list[current]: | ||
| if connection[1] not in seen: | ||
| heapq.heappush(connection_queue, connection) | ||
|
|
||
| return res | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| #### Final Code: | ||
|
|
||
| <Tabs> | ||
| <TabItem value="py9" label="Python"> | ||
| <SolutionAuthor name="@Infonioknight"/> | ||
|
|
||
| ```py | ||
| import heapq | ||
|
|
||
| class Solution: | ||
| def min_cost_points(self, adjacency_list, initial): | ||
| # Number of nodes in the given tree | ||
| n = len(adjacency_list) | ||
| # A list we will use to implement a priority queue | ||
| connection_queue = [] | ||
| # Total minimum cost to connect all points | ||
| res = 0 | ||
| # Taking the assumption that the n nodes in the adjacency list are from 1 to n | ||
| start = tuple(initial) | ||
| # To ensure we don't create closed loops | ||
| seen = set([start]) | ||
|
|
||
| for connection in adjacency_list[start]: | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| heapq.heappush(connection_queue, connection) | ||
|
|
||
| while len(seen) < n and connection_queue: | ||
| cost, current = heapq.heappop(connection_queue) | ||
| if current in seen: | ||
| continue | ||
|
|
||
| res += cost | ||
| seen.add(current) | ||
|
|
||
| for connection in adjacency_list[current]: | ||
| if connection[1] not in seen: | ||
| heapq.heappush(connection_queue, connection) | ||
|
|
||
| return res | ||
|
|
||
| def minCostConnectPoints(self, points: List[List[int]]) -> int: | ||
| adjacency_list = {} | ||
| for i in range(len(points)): | ||
| current = tuple(points[i]) | ||
| for j in range(i+1, len(points)): | ||
| destination = tuple(points[j]) | ||
| if current not in adjacency_list: | ||
| adjacency_list[current] = [] | ||
| if destination not in adjacency_list: | ||
| adjacency_list[destination] = [] | ||
|
|
||
| adjacency_list[current].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), destination]) | ||
| adjacency_list[destination].append([abs(destination[0] - current[0]) + abs(destination[1] - current[1]), current]) | ||
|
|
||
| if len(points) < 2: | ||
| return 0 | ||
| return self.min_cost_points(adjacency_list, points[0]) | ||
| ``` | ||
| </TabItem> | ||
| </Tabs> | ||
|
|
||
| export const suggestedProblems = [ | ||
| { | ||
| "problemName": "1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree", | ||
| "difficulty": "Hard", | ||
| "leetCodeLink": "https://leetcode.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/", | ||
| "solutionLink": "" | ||
Infonioknight marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| }, | ||
| { | ||
| "problemName": "0787 - Cheapest Flights Within K Stops", | ||
| "difficulty": "Medium", | ||
| "leetCodeLink": "https://leetcode.com/problems/cheapest-flights-within-k-stops/", | ||
| "solutionLink": "../../solutions/0700-0799/0787-cheapest-flights-within-k-stops-medium.md" | ||
wingkwong marked this conversation as resolved.
Show resolved
Hide resolved
|
||
| }, | ||
| ] | ||
|
|
||
| <Table title="Suggested Problems" data={suggestedProblems} /> | ||
Add this suggestion to a batch that can be applied as a single commit.
This suggestion is invalid because no changes were made to the code.
Suggestions cannot be applied while the pull request is closed.
Suggestions cannot be applied while viewing a subset of changes.
Only one suggestion per line can be applied in a batch.
Add this suggestion to a batch that can be applied as a single commit.
Applying suggestions on deleted lines is not supported.
You must change the existing code in this line in order to create a valid suggestion.
Outdated suggestions cannot be applied.
This suggestion has been applied or marked resolved.
Suggestions cannot be applied from pending reviews.
Suggestions cannot be applied on multi-line comments.
Suggestions cannot be applied while the pull request is queued to merge.
Suggestion cannot be applied right now. Please check back later.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
can you also work on MST page?
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Will try in a bit once work eases up a little. Hope that's okay.